Распределение хи-квадрат, Стьюдента, Фишера

Дисперсионный анализ.

Опр: Дисперсионным анализом наз. статистический метод анализа результатов измерений, зависящих от различных одновременно действующих факторов. Ограничимся рассмотрением простейшего случая, когда действует один фактор. Пусть, например, выборка разбита на r групп, причем i-ая группа содержит 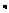величин 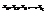Предположим, что все указанные величины распределены нормально и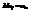 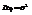, j=1,…, 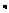; i=1,…,r. Нам нужно проверить гипотезу 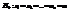. В физической постановке эта задача выглядит так: одна и та же величина a измеряется r различными приборами, имеющими одинаковую точность. Нас интересует, имеют ли приборы различные систематические ошибки. В рассматриваемом примере исследуется влияние одного фактора (прибора) на погрешность измерения. Введем обозначения: 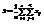, , n= . 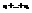Групповые средние 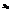являются несмещенными и состоятельными оценками величин 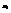. Если все 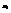одинаковы, то общая средняя 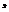не должна сильно отличаться от групповых. В противном случае разброс 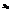относительно 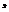будет достаточно значительным. 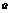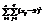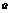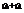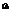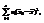Представим общую, или полную, сумму квадратов отклонений: = (1) в следующем виде: = (2), где = = 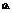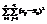(3). Опр.: Сумму 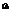наз. суммой квадратов отклонений “между группами”, 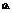- суммой квадратов отклонений “внутри групп”.

Методы расчета сводных характеристик выборки. Условные варианты. Обычные, начальные и центральные эмпирические моменты.

Предпол., что варианты выборки расположены в возрастающем порядке, т.е. в виде вариационного ряда. Опр.: Равностоящими наз. варианты, кот. образуют арифметическую прогрессию с разностью h. Опр.: Условными называют варианты, определяемые равенством: 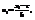С - ложный нуль(новое начало отсчета); h - шаг, т.е. разность между любыми двумя соседними первоначальными вариантами( новая единица масштаба). Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными. Покажем, что если вариационный ряд состоит из равностоящих вариант с шагом h , то условные варианты есть целые числа. Действительно, выберем в качестве ложного нуля произвольную варианту, напр. 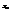, тогда 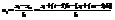= 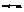Т.к. i и m –натуральные числа, то i-m= 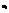- целое число. Замечание 1. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, кот. расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту). Замечание2. Варианте, кот. принята в качестве ложного нуля, соответствует условная варианта, равная 0.

Условные эмпирические моменты. Отыскание центральных моментов по условным. Метод произведения.

Вычисление центральных моментов требует довольно громоздких вычислений. Чтобы упростить расчеты, заменяют первоначальные варианты условными. Опр.: Условным эмпирическим моментом порядка к наз. начальный момент порядка к, вычисленный для условных вариант: 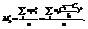В частности, 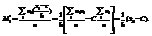Т.о., чтобы найти выборочную среднюю, достаточно вычислить условный момент первого порядка, умножить его на h и к результату прибавить ложный нуль С: 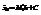. По определению, условный момент к-го порядка 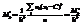. Отсюда 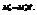Т.о. чтобы найти обычный момент порядка к, нужно условный момент того же порядка умножить на 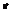. Выборочная дисперсия вычисляется по формуле: 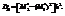Метод произведения.Метод произведений даёт удобный способ вычисления условных моментов различных порядков для вариационного ряда с равностоящими вариантами. Зная условные моменты, нетрудно найти начальные и центральные эмпирические моменты. В частности, методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Целесообразно пользоваться расчетной таблицей, которая составляется так: 1) в 1-ый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке; 2) во 2-ой столбец записывают частоты вариант; складывают все частоты и их сумму(объем выборки n) помещают в нижнюю клетку столбца; 3) в 3-ий столбец записывают условные варианты 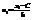, причем в качестве ложного нуля С выбирают варианту, кот. расположена примерно в середине вариационного ряда, и полагают h = разности между любыми двумя

25. Корреляционная таблица. Вычисления выборочного коэффициента корреляции.

Пусть имеются результаты наблюдений для случайного вектора (Х, У). При большом объеме выборки одно и то же значение х СВ Х может встречаться 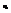раз , а одно и то же значение у СВ У может встречаться 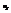раз, одна и та же пара чисел (х,у) может наблюдаться 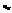раз. Поэтому данные наблюдений группируют, т.е. подсчитывают частоты 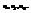Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной. В соответствии с введенными обозначениями, выборочный коэф-т корреляции определяется равенством: 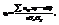где x и y –наблюдаемые значения СВ X и Y , 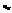- частота появления пары (x,y); n- объем выборки (сумма всех частот); 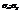-выборочные средние квадратические отклонения ( 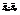-неисправленные выборочные дисперсии); 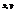-выборочные средние. Пусть требуется по данным корреляционной таблицы вычислить

Метод наименьших квадратов.

Выборочное уравнение линейной регрессии можно получить методом наименьших квадратов, если положить, что 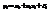, где 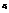-некоторая ошибка измерений, 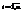Метод наименьших квадратов или метод Гаусса сводиться к тому, что коэффициенты 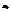и 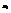нужно искать из того условия, что сумма квадратов ошибок по всем наблюдениям стремится к минимуму, т.е.

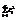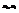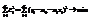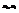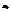→min. Для этого составляется функция F( )= . Берутся частные производные от F( ) по и 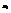и приравниваются к 0.

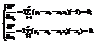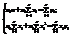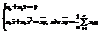; ; , т.е. получили систему из двух линейных уравнений с двумя неизвестными a₀ и a₁. Решив ее, получим уравнение линейной регрессии Y на X вида: .

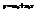Распределение хи-квадрат, Стьюдента, Фишера

О.1Случайная величина 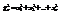, где случайные величины 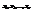- независимы и имеют стандартное нормальное распределение (т.е. N(0,1)), называется случайной величиной хи-квадрат с n степенями свободы.

Обозначим через 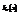- плотность вероятности случайной величины 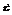, а через 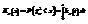-функцию распределения случайной величины 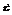. На основании этих функций составлена таблица процентных точек распределения 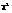. Рассмотрим следующее уравнение: 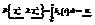(1) . Решение 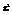в уравнении (1) называется критической точкой распределения 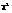, соответствующей уровню значимости 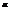и числу степеней свободы n.

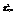- процентная точка, соответствующая числу степеней свободы и уровню значимости 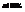. О.2.Отношение 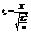, где X~N(0,1) -имеет стандартное нормальное распределение, а числитель и знаменатель - независимые CB, называется отношением Стьюдента с n степенями свободы. Обозначим через 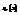плотность вероятности СВ 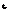, а через 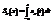- функцию распределения случайной величины .

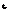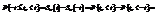
. (2). Пусть необходимо решить уравнение: 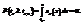, здесь 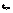называется критической (процентной) точкой распределения Стьюдента, соответствующей числу степеней свободы n и уровню значимости 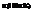. О.3.Отношение 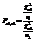, где числитель и знаменатель – независимые СВ, называется F – отношением или отношением Фишера.

Обозначим через 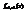плотность вероятности СВ .

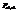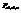- называется критической (%-ной) точкой F – распределения, соответствующей числам степеней свободы n₁и n₂и уровню значимости .

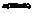Дата добавления: 2018-05-13; просмотров: 548; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 Следующая ⇒

Мы поможем в написании ваших работ!