Математическое ожидание и его св-ва.

Мат–ое ожиданием дискретной СВ наз-ся сумма произведений всех ее значений на их вероятности и обозначается М(Х).

Если дискретная СВ Х принимает значение х_1,х_2,…,х_n с соотв-щими вероятностями р_1,р_2,…р_n_, то ее мат ожидание вычисляется по форлуле:

М(Х)= х_1*р₁₊х_2*р₂₊…₊х_n_*_pn

Если дискретная СВ Х принимает счетное множество значений х_1,х_2,…,х_n_,…с соответ-щей вероятностью р_1,р_2,…,р_n_,…,то мат ожидание вычисляется по фор-ле:

∞

М(Х)= ∑ х_i_*p_i причем

i=1

числовой ряд сходится обсолютно.

Счетное множество-бесконечное множ-во, кот-ое можно записать в виде бесконечной числовой последовательности.

Опре-ие: мат ожидание непрерывной СВ Х, значение которой принадлежат отрезку [а,в], наз-ся число равное определенному интегралу:

М(Х)=∫x f(x) dx

Если значение непрер-ой СВ Х принадлежит всей числовой оси, то мат ожидание вычисляется:

+∞

М(Х)=∫x f(x) dx

-∞

причем этот несобственный интеграл сходится абсолютно(т.е сущ-ет интеграл от модулей подинтегр-ой фун-ции:

+∞

∫ (хf(x)dx)

-∞

Осн св-ва мат ожидания:1. мат ожидание постоянной СВ равно самой постоянной М(С)=С

2.постоянный множитель можно выносить за знак мат ожидания М(СХ)=СМ(Х)

3.мат ожидание суммы 2-ух СВ равно сумме мат ожидания этих величин М(Х+У)=М(Х)+М(У)

4.мат ожидание произведения 2-ух независимых СВ равно произведению их мат ожиданий

М(Х*У)=М(Х)*М(У)

Теорема2 мат ожидание дискретной СВ, распределенной биномиально равно М(Х)=р*n, где n-число испытаний в схеме Бернули, р-вероятность успеха в схеме Бернулли.

13. Дисперсия и ее св-ва. Среднее квадратическое отклонение. Дисп. СВ Х наз-ся мат. ожидание квадрата отклонения этой СВ от ее мат. ожидания и обознач. Д(Х). Д(Х)=М[X- М(Х)]². Д/дискретных СВ дисп-ия вычисляется Д(Х)=(х₁-М(Х))²×р₁+(х₂-М(Х))²×р₂+…+(х_n – М(Х))²×р_n. Дисп. СВ всегда неотриц. число и чем меньше она, тем меньше рассеивание ее величины. Т3: дисп. СВ Х равна разности м/у мат. ожид. квадрата этой СВ и квадратом ее мат. ожид. Д(Х)=М(Х²)- [M(X)]². Если возможные значения непрерывной СВ принадлежат отрезку АВ, то дисп. этой величины вычисляется Д(Х)=^в_аò (х- М(Х))²×f(x)dx. Если значения непрер. СВ принадлежат всей числовой оси, т.е. интервалу (-∞;+∞), то ее дисп. вычисл. с помощью несобственного интеграла Д(Х)=^-_+∞^∞ò(х-М(Х))²× f(x)dx. Средним квадрат. отклонением СВ наз-ся неотриц. число G(x) . G(X)=√Д(Х). Св-ва дисп: 1. Д(С)=0, 2. Д(СХ)=С²Д(Х), 3. Д(Х+У)=Д(Х)+Д(У), 4. Д(Х-У)=Д(Х)+Д(У), 5. Д(Х)=n×p×q- дисп. распределена по биноминальному закону.

14. Мода и медиана. Модой непрер. СВ Х наз. ее возможное значение, при кот. плотность распред-ия f(x) достигает мах значение М₀(Х).

МедианойМ_е(Х) непрер. СВ Х наз. такое ее значение, что вер-ть того, что СВ примет значение меньше медианы равняется вер-ти того, что СВ больше медианы и равна ½. Р(Х<М_е)= Р(Х>М_е)=1/2.

15. Равнометное распределение. Бином. рапред. Непрер. СВ Х имеет равномерн. з-н распред. на [a, в], если плотность распред-ия. f(x) постояна на этом отрезке и равна 0 вне его. Можно показать,что д/СВ расперд-ой по равномер. з-ну плотность распред-ияимеет вид 0, х<а

f(x)= 1/(в-а), а≤Х≤в

0, Х>в.

А ф-ия распред-ия имеет вид 0, Х≤а

F(X)= (х-а)/(в-а), а<Х≤в

1, Х>в.

СВ распред- ая по равномер. з-ну обладает след. св-ом: вер-ти того, что значение СВ нах-ся в числовых промежутках равной длины равны.

16. нормальное распределение СВ, основные хар-ки. Непрер. СВ Х имеет нормальный з-н расперд-ия ( з-н Гаусса) с параметрами а и G², если ее плотность распред-ия имеет вид

f(x)= 1/G√2П×e^{–((х-а)^2)/ 2(G^2)}. Нормальн. расперд-ие опр-ся 2-мя параметрами а и G², причем М(Х)=а, Д(Х)=G². Ф-ия расперд-ия норм. СВ имеет вид

F(X)=1/G√2П× ^x_-∞ò e^-((^t^-^a^{)^2)/2(}^G^{^2)}dt. Ф-ию распред-ия непрер. СВ распред-ой по норм. з-ну можно выразить и ч/з ф-ию Лапласа Ф(Х) F(x)=1/2+ Ф((x-a)/G), где ф-ия Лапласа опр-ся

Ф(Х)= 1/√2П×^х₀ò e^–(^t^{^2)/2}dt.

Тогда вер-ть попадания значения СВ Х в отрезок [a,b] выч-ся Р(a≤Х≤b)= F(b)-F(a)= Ф((b-а)/G)-

Ф(( a-а)/G). Значение по спец. табл.

Т4: если СВ Х имеет норм. з-н распред-ия с параметрами а, G² , то практически достоверно, что ее значения заключены в интервале (а- 3G, a+ 3G),т.е. вер-ть Р(|x-a| <3G)= 2Ф(3)=0,9973.

17.Опред.Непрерывная случайная величина X, функция плотности которой задается выражением называется случайной величиной, имеющей показательное, или экспоненциальное, распределение.

Как видно из формулы , показательное распределение определяется только одним параметром .

Найдем функцию распределения показательного закона, используя свойства дифференциальной функции распределения:

Графики дифференциальной и интегральной функций показательного распределения имеют

Числовые характеристики

Используя формулы для вычисления математического ожидания, дисперсии и среднего квадратического отклонения нетрудно убедится, что для показательного распределения

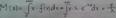
Таким образом, для показательного распределения характерно, что среднее квадратическое отклонение численно равно математическому ожиданию.

Найдем вероятность попадания непрерывной случ. величины распределения по числовому закону в интервал (a,b)

18. Лемма 1.(Чебышева-Маркова). Если значение случайной величины х неотрицательно и существует её мат. ожидание М(х)=а, то для любого положительного числа >0 имеет место неравенство:

P(Х ) (1)

Неравенство (1) называют неравенством Чебышева-Маркова. Очевидно, чем > и меньше а, тем более вероятнее, что Х .

Обобщенное неравенство Чебышева. Пусть – неотрицательная и неубывающая функция такая, что

P(|X| .

Дата добавления: 2018-05-13; просмотров: 283; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 Следующая ⇒

Мы поможем в написании ваших работ!