Теорема Бернуллі.(доведення).
Нехай проводиться n незалежних повторних випробувань, у кожному з яких імовірність настання події А дорівнює р.Якщо ймовірність появи випадкової події А в кожному з незалежних випробувань n є величиною сталою і дорівнює P,то при необмеженому збільшенні числа експериментів n→∞
Імовірність відхилення відносної частоти появи випадкової події W(A) від імовірності p ,взятої за абсолютною величиною на ε(ε>0) прямуватиме до одиниці зі зростанням n ,що можна записати так:
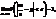
де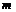 
— частота події А у даних випробуваннях. Таким чином при необмеженому збільшенні числа незалежних випробувань за схемою Бернулі відносна частота дуже мало відрізняється від ймовірності .
Наведена теорема є законом великих чисел ,так само як і центральна гранична теорема
Центральна гранична теорема.
Для послідовності випадкових величин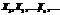 
розглянемо:
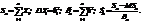
Теорема. Якщо випадкові величини в послідовності незалежні, однаково розподілені і для них існують моменти другого порядку, то
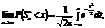
тобто граничним розподілом для 
є нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.
Теорема Ляпунова. Якщо для незалежних випадкових величин, які утворюють послідовність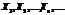 
, існують моменти третього порядку і виконується умова
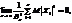то для 
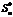виконується співвідношен-
ня (2).
Наслідком розглянутих теорем є інтегральна теорема Лапласа.
У схемі незалежних повторних випробувань
|
|
|
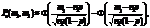
де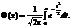 
Це випливає з того, що частоту події можна подати як суму n випадкових величин — частот настання події в окремих випробуваннях. При достатньо великих значеннях n закон розподілу цієї суми близький до нормального.
Аналогічними міркуваннями для цієї схеми легко дістати формулу:
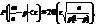де m — частота події А у n випробуваннях.
Генеральна та вибіркова сукупність. Співвідношення чисельних характеристик.
Генеральною сукупністю в математичній статистиці називається множина однотипних об’єктів, кількісна чи якісна ознака яких підлягає вивченню. Підмножина об’єктів, дібраних у відповідний спосіб із генеральної сукупності, називається вибірковою сукупністю. Вважаємо, що ознака, яка вивчається, є випадковою величиною Х із функцією розподілу 
Результати вибірки розглядатимемо як послідовність незалежних однаково розподілених випадкових величин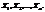 
Закон розподілу для всіх 
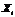визначається функцією 
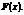Результати вибірки — реалізації випадкових величин — позначатимемо відповідно через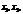 
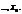Розмістивши ці числа в порядку зростання і записавши частоти 
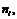з якими зустрічаються ці значення, дістанемо варіаційний, або статистичний, ряд:
|
|
|
| 
| 
| … | 
|
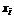
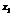
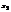
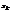
| Частоти |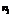 
| 
| … | 
|
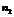
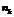
На підставі такого ряду можна побудувати статистичну функцію розподілу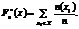 
Якщо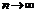 
, то статистична функція розподілу збігається д теоретичної функції розподілу.
Дата добавления: 2018-05-13; просмотров: 210; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!