Поняття моди у експериментах за схемою Бернуллі.

В деяких задачах виникає необхідність знаходити найімовірніше число появи випадкової події(мода). Тобто це таке число появи випадкової події А в результатінезалежних експериментів за схемою Бернуллі - m_o, для якого ймовірність Р_n(m_о) перевищує або в усякому разі є не меншою за ймовірність кожного з решти можливих ймовірностей Р_n(m) наслідків експериментів.

Зауважимо, що для визначення найімовірнішого числа появи події немає потреби обчислювати ймовірності для різних можливих значень m (0 ≤ m ≤ n). Щоб набути це число, розглянемо відношення:

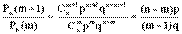
Якщо послідова ймовірність Р_n(m + 1) більше попередньої Р_n(m), то - це відношення не менше одиниці; якщо Р_n(m + 1) £ Р_n(m), то не більше одиниці. Таким чином маємо

 

 

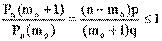
і тоді m_o ³ np - q, а якщо

 

 

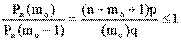
тоді m_o ³ np + р.

Якщо об'єднати ці нерівності, дістанемо:

np -q≤m_o≤np +р.Число m_o називають також модою.

 

Локальна теорема Мавра-Лапласа.

Імовірність того, що в n незалежних випробуваннях, у кожному з яких Р(А) = р, подія А відбудеться m раз, подається такою наближеною залежністю:

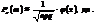
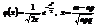
Локальна теорема Лапласа дає змогу обчислювати ймовірності 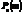, якщо n > 10 i p > 0,1.

 

Інтегральна теорема Лапласа.

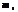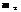Імовірність того, що подія А відбудеться від  до  раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, подається формулою:

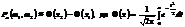 —функція Лапласа;

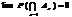
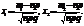
Значення функції Лапласа наводяться у спеціальних таблицях.

Теорема Лапласа для відхилення частоти появи події від моди.

Теорема Лапласа для відхилення ймовірностей від частоти.

Формула Пуассона для малоймовірних подій.

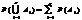
Точність асимптотичних формул для великих значень n- числа повторних незалежних експериментів за схемою Бернуллі – знижується з наближенням p- до нуля .Тому при n → R,

p- 0 за умови np=a=const імовірність появи випадкової події m раз

(0<=m <=n),обчислюється за такою асимптотичною формулою:

Якщо в кожному з n незалежних повторних випробувань 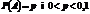, а n велике, то

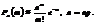
Функція Гауса її властивості і використання в схемах Бернуллі.

У математиці функцією Гауса є функція, що виражається залежністю

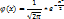
Графік функції Гауса є характерною симетричною кривою у формі дзвону, що швидко спадає на нескінченності. Параметр a є висотою піку кривої, b є позицією центру, і c контролює ширину «дзвону».

Визначений інтеграл від ґаусової функції дає функцію помилок

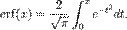
Визначений інтеграл з нескінченними границями має властивість

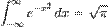
Цей інтеграл рівний 1 тоді і тільки тоді, коли a = 1/(c√(2π)), і в цьому випадку Гаусіан є щільністю нормального розподілу випадкової величини з математичним очікуванням μ=b ідисперсією σ²=c².

При перетворенні Фур'є функції Гауса з параметрами a, b=0 і c отримуємо іншу функцію Гауса, з параметрами ac, b=0 і 1/c. Отже, як частковий випадок, функція Гауса з b=0 і c=1 єінваріантом щодо перетворення Фур'є (вони є власними функціями перетворення Фур'є з власним значенням 1).

---

Дата добавления: 2018-05-13; просмотров: 240; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!