Основные методы решения систем двух неравенств с двумя неизвестными

⇐ ПредыдущаяСтр 7 из 23Следующая ⇒

1. Метод подстановки. В каком-либо неравенстве выражаем одну неизвестную через другую и подставляем в другое неравенство с целью исключения одной неизвестной.

2. Метод сложения. В результате умножения одного из неравенств системы на число и прибавления ко второму неравенству, получается равносильная система. Метод используют с целью, чтобы в результате сложения одна из неизвестных исчезла или было получено более простое неравенство.

3. Графический метод. Строят графики функций (или кривые), которые соответствуют уравнениям системы. Находят координаты точек пересечения этих графиков. Данным метод решения не всегда дает точное решение.

Эти приемы обобщаются на решение систем с большим количеством уравнений и неизвестных.

4.Метод интервалов

Иррациональные уравнения. Основные методы решения иррациональных уравнений

Иррациональным уравнениемназывается уравнение, содержащее неизвестную под знаком корня или под дробным показателем. (В этом параграфе термин «корень» будет соответствовать операции извлечения корня с определенным показателем, в отличие от термина «решение»).

Основной метод решения таких уравнений – возведение обеих частей уравнения в одну и ту же степень, чтобы корни исчезли. Иногда приходится возводить в степень несколько раз. При этом следует анализировать, какие корни надо оставлять в левой части уравнения, а какие корни перенести в правую часть (если корней несколько). От этого часто зависит рациональность решения.

Поскольку корни нечетной степени определены для любых по знаку подкоренных выражений и принимают любые по знаку значения, то возведение уравнения в нечетную степень является равносильным преобразованием (т. е. мы не теряем решений и не получаем посторонних).

Корни с четным показателем определены для f(x)³ 0. Возведение уравнения, содержащего такие корни, в четную степень может изменить ОДЗ уравнения и привести к посторонним решениям. В таком случае итоговым моментом в решении уравнения является проверка полученных решений подстановкой в заданное уравнение. Проверка решения по ОДЗ такого уравнения недостаточна.

ОДЗ иррационального уравнения следует находитьв том случае, если предполагается, что она состоит только из нескольких чисел или может быть пустым множеством. Если ОДЗ состоит из одного, двух и т. д. чисел, то уравнение можно не решать, а эти числа проверять (являются ли они решением) подстановкой в заданное уравнение.

Если ОДЗ есть пустое множество, то уравнение не имеет решений.

При решении иррациональных уравнений используют также метод замены переменной и другие методы.

Если имеется уравнение вида где с < 0, то оно не имеет решений, так как корни с четным показателем понимаем в арифметическом смысле, т. е. как неотрицательные.

Некоторые типы иррациональных уравнений

Пусть далее 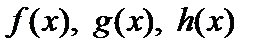– некоторые выражения с неизвестной х,

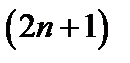I тип: уравнение вида (1). Возведение в -ю степень приводит к равносильному уравнению

Уравнение (2) после возведения в -ю степень сводится к равносильному уравнению

Уравнение (3) после возведения в степень 2n приводит к уравнению-следствию (4)

Найденные корни уравнения (4) проверяют подстановкой в уравнение (3) и отбирают те из них, которые удовлетворяют уравнению (3).

Уравнение (5) после возведения в степень 2n сводится к уравнению-следствию (6)

Корни уравнения (5.6) необходимо проверить подстановкой в уравнение (5).

II тип: уравнение вида (7) где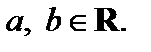

1-й способ. Необходимо возвести уравнение (7) в квадрат. В определенных случаях следует один из корней перенести в правую часть уравнения. После упрощения полученное уравнение возводят в квадрат еще раз.

2-й способ. Умножение уравнения (7) на сопряженное выражение

Отдельно проверяют, имеет ли решение уравнение h(x) = 0. Затем для h(x) ¹ 0 рассматривают систему

Сложение уравнений этой системы приводит к уравнению вида (3).

3-й способ. Замена переменных

и переход к системе уравнений относительно u, v.

Уравнение (8) где a, b Î R, возведением в куб обеих частей сводится к уравнению (9)

Выражение в скобках (в левой части уравнения (5.9)) заменяют на используя заданное уравнение. В итоге заданное уравнение (8) приводится к уравнению-следствию, которое снова возводят в куб.

Полученные таким образом решения необходимо проверить подстановкой в уравнение (8).

III тип: уравнения, решаемые заменой переменной.

В результате замены может уменьшиться степень выражений, стоящих под корнями, что приведет к уменьшению степени рационального уравнения после избавления от корней.

Если уравнение имеет вид (10) где F – некоторое алгебраическое выражение относительно то заменой 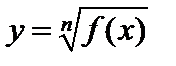оно сводится к уравнению (11)

После решения уравнения (5.11) возвращаются к старой переменной и находят решения уравнения (10).

IV тип: уравнения, решаемые исходя из арифметического смысла корней с четными показателями. В частности, решение уравнения (12)

где a > 0, b > 0, сводится к решению системы

V тип: уравнения, решаемые функциональными методами и методами, основанными на ограниченности входящих в уравнение функций.

Решение уравнений основывается на следующих утверждениях.

1. Есл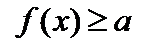и и для всех , то на множестве X уравнение f(x) = g(x) равносильно системе уравнений

2. Если функции f(x) и g(x) непрерывны и f(x) возрастает, а g(x) убывает для x ÎX, то уравнение f(x) = g(x) имеет не больше одного решения на промежутке X. Если один корень подобрать, то других корней нет.

3. Если f(x) – возрастающая функция, то уравнение 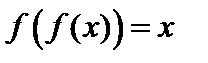равносильно уравнению

4. Если f(x) – возрастающая (убывающая) функция, то уравнение равносильно уравнению

Дата добавления: 2018-05-13; просмотров: 596; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!