Использование монотонности функций.

Если на некотором промежутке  функции  и , входящие в уравнение 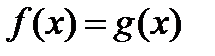 таковы, что  непрерывна и возрастает, а  непрерывна и убывает, то равенство 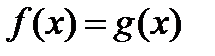 возможно только при единственном значении 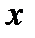, которое и является корнем данного уравнения на рассматриваемом промежутке. Иногда этот корень можно найти подбором.

6. Иногда корень уравнения можно найти, заметив, что функция, находящаяся в одной из его частей, является суперпозицией нескольких более простых функций.

В частности, если  корень уравнения , то  является также корнем уравнений  и т.д.

7. Графический метод. Иногда полезно рассмотреть эскизы графиков функций  и , входящих в уравнение 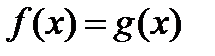. Этот метод, не являющийся строгим решением, может помочь установить:

а) существуют ли у данного уравнения корни и сколько их;

б) на какие множества следует разбить область определения уравнения, чтобы на каждом из этих множеств использовать свой способ решения.

 

 

Рациональные неравенства и методы их решения

Пусть f(x)=0 ( числовая функция одного или нескольких переменных (аргументов). Решить неравенство (f(x) < 0      f(x) > 0 (1) (это значит найти все значения аргумента (аргументов) функции, при которых неравенство (1) справедливо. Множество всех значении аргумента (аргументов) функции, при которых неравенство (1) справедливо, называется множеством решении неравенства или просто решением неравенства.

Два неравенства считаются эквивалентными, если множества их решении совпадают.

  Под множеством допустимых значений неизвестных, входящих в неравенство, понимают область определения функции f(x)=0.

Неравенства вида (1), составленные для различных функции f(x)=0, могут быть сведены в систему неравенств. Решить систему неравенств – это значит найти множество всех значении аргументов функции f(x), при которых справедливы все неравенства системы одновременно.

Говорят, что системы неравенств эквивалентны, если множества их решении совпадают.

Алгебраические неравенства.

Линейными (строгими и нестрогими) называются неравенства вида

      ax + b > 0, ax + b < 0 (ax + b>=0, ax + b<=0)

Квадратными (строгими и нестрогими) называются неравенства вида

   ax² + bx + c > 0, ax² + bx + c < 0,

   ax² + bx + c >= 0, ax² + bx + c <= 0, где a, b, c – некоторые действительные числа и а ≠ 0.

Квадратное неравенство ax² + bx + c > 0 в зависимости от значения своих коэффициентов a, b и c имеет решения:

при а > 0 и D = b² – 4ac ≠0 , то х принадлежит интервалу

при а > 0 и D < 0 x – любое действительное число;

при а < 0 и D ≠0      x(( –х₁  ; ;х₁ ) );

при а < 0 и D < 0        x = ( (т. е. решении нет ).

Решение неравенства ax² + bx + c < 0 сводится к решению рассмотренного неравенства, если обе части неравенства умножить на (–1).

---

Дата добавления: 2018-05-13; просмотров: 313; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!