Преобразования, приводящие к равносильному уравнению
(Область определения исходного уравнения обозначена через 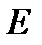 , область определения функции
, область определения функции  – через
– через  , причем предполагается, что
, причем предполагается, что 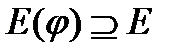 ):
):
1) 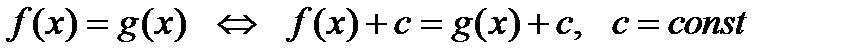 ;
;
2) 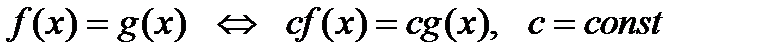 ;
;
3) 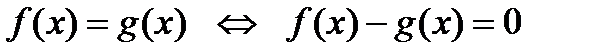 ;
;
4) 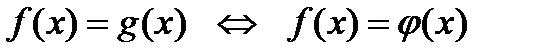 , если для любого
, если для любого 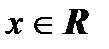 справедливо тождество
справедливо тождество 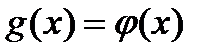 ;
;
5) 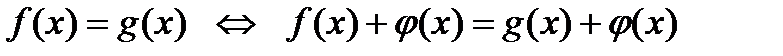 , где
, где 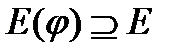 ;
;
6) 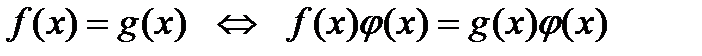 , где
, где 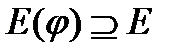 ,
, 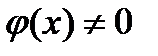 для
для 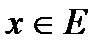 ;
;
7) 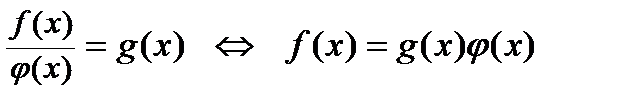 при
при 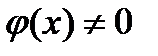 для
для 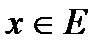 ;
;
8) 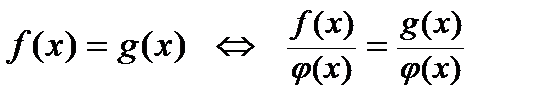 , где
, где 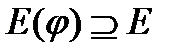 ,
, 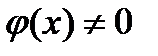 для
для 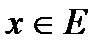 ;
;
9) 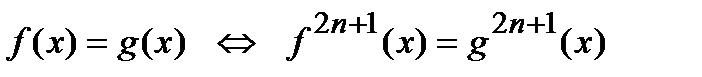 ,
,  ;
;
10) 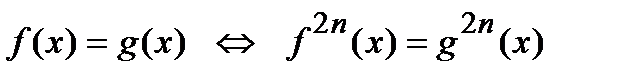 ,
,  , если
, если 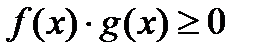 для любого
для любого 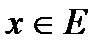 (т.е. если функции
(т.е. если функции 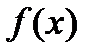 и
и 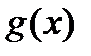 имеют в области
имеют в области 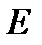 одинаковые знаки);
одинаковые знаки);
11) 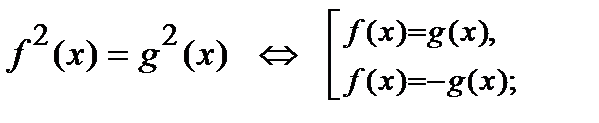
12) 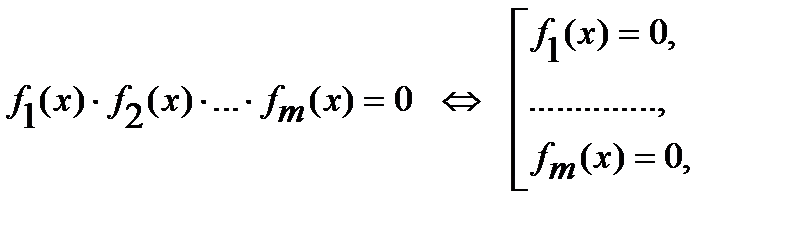 для
для 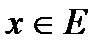 ;
;
13) 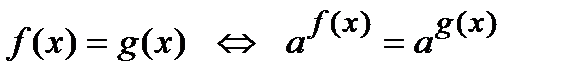 , если
, если 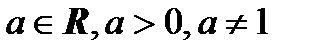 ;
;
14) 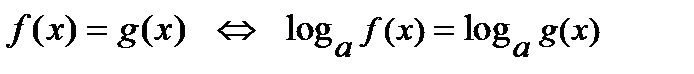 , если
, если 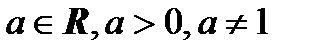 и на области определения уравнения
и на области определения уравнения 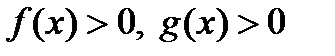 .
.
Теоремы о равносильных преобразованиях уравнений
теорема1: если к обеим частям уравнения f(x)=g(x) прибавить одно и то же выражение с(х), которое имеет смысл при всех х из области определения уравнения, то получаем равносильные уравнения:
f(x)+c(x)=g(x)+c(x). Док–во производится на основании свойств 1, 3, 5.
теорема2: если обе части уравнения f(x)=g(x) умножить на одно и то же вырадение с(х), которое имеет смысл при всех х из области определения уравнения и нигде в этой области не преобразовывается в ноль, то получаем равносильные уравнения:
f(x)*c(c)=g(x)*c(x) _ f(x)=g(x)
f(x)/c(x)=g(x)/c(x) _ f(x)=g(x)
Док–во производится на основании свойств 2, 6
6. Неравенства. Равносильные неравенства. Неравенства-следствия.
Теоремы о равносильных преобразованиях неравенств
Пусть f(x)=0 ––– числовая функция одного или нескольких переменных(аргументов). Решить неравенство (f(x) < 0 f(x) > 0 (1)
(это значит найти все значения аргумента (аргументов) функции, при которых неравенство (1) справедливо. Множество всех значении аргумента (аргументов) функции (, при которых неравенство (1) справедливо, называется множеством решении неравенства или просто решением неравенства.
|
|
|
Два неравенства считаются эквивалентными, если множества их решении совпадают.
Под множеством допустимых значении неизвестных, входящих в неравенство, понимают область определения функции f(x)=0.
Неравенства вида (1), составленные для различных функции f(x)=0, могут быть сведены в систему неравенств. Решить систему неравенств – это значит найти множество всех значении аргументов функции f(x), при которых справедливы все неравенства системы одновременно.
Говорят, что системы неравенств эквивалентны, если множества их решении совпадают.
Теоремы о равносильных преобразованиях неравенств
При решении неравенств используют свойства равносильности.
Неравенства с одной переменной называются равносильными, если множества их решении совпадают.
Например, неравенства 3х > 6 и х – 2 > 0 имеют одинаковые множества решении. Эти неравенства – равносильные.
При решении неравенств выполняются только такие преобразования, при которых получаются более простые равносильные неравенства. Эти преобразования возможны при выполнении следующих свойств равносильных неравенств.
|
|
|
Теорема 1. Если к обеим частям неравенства прибавить одно и то же число или одно и то же выражение, которое имеет смысл при всех значениях переменной, то получим неравенство, равносильное данному.
Дано. Р(х) > Q(x) – неравенство, Т(х) – выражение, которое имеет смысл при всех действительных значениях х, х 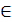 R.
R.
Доказать. Неравенства Р(х) > Q(x) и Р(х) + Т(х) > Q(x) + T(x) – равносильные.
Доказательство. а) Пусть при х = а неравенство Р(а) > Q(a) – верное числовое равенство, т.е. х =а – одно из решении неравенства Р(х) > Q(x), Т(а) – значение Т(х) при х =а. По свойству числовых неравенств Р(а) + Т(а) > Q(a) + T(a) – верное числовое неравенство.
Следовательно, х = а – одно из решений неравенства Р(х) + Т(х) > Q(x) + T(x). Поэтому, если х =а есть решение первого неравенства, то это значение есть также решение второго неравенства.
б) Пусть х = b – одно из решений неравенства Р(х) + Т(х) > Q(x) + T(x), т.е.
P(b) + T(b) > Q(b) + T(b) –верное числовое неравенство. По свойству числовых неравенств P(b) > Q(b) – тоже верное числовое
неравенство. Следовательно, х = b – решение неравенства P(x) > Q(x). Так как множества решений неравенства P(x) > Q(x) и P(x) + T(x) > Q(x) + T(x) совпадают, то эти неравенства равносильные.
|
|
|
Теорема 2. Если в неравенстве любое слагаемое, которое имеет смысл при всех х 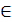 R, перенести из одно части в другую с противоположным знаком, то получим неравенство, равносильно данному.
R, перенести из одно части в другую с противоположным знаком, то получим неравенство, равносильно данному.
Дано. P(x) + T(x) > Q(x) – неравенство, Т(х) – слагаемое, которое имеет смысл при всех х 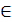 R.
R.
Доказать. Неравенства P(x) + T(x) > Q(x) и P(x) > Q(x) – T(x) – равносильные.
Доказательство. По свойству 1 можно к обеим частям неравенства
P(x) + T(x) > Q(x) прибавить слагаемое (– Т(х)), так как это слагаемое имеет смысл при всех х 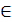 R; получим равносильное неравенство: P(x) + T(x) – T(x) > Q(x) – T(x), отсюда P(x) > Q(x) – T(x).
R; получим равносильное неравенство: P(x) + T(x) – T(x) > Q(x) – T(x), отсюда P(x) > Q(x) – T(x).
Теорема 3. Если обе части неравенства умножить на одно и то же положительное число или на одно и то же выражение, положительное при всех значениях переменной, то получим неравенство, равносильное данному.
Дано. P(x) > Q(x) – неравенство (1),
T(x) > 0, x 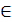 R, P(x)(T(x) > Q(x)(T(x) – неравенство (2).
R, P(x)(T(x) > Q(x)(T(x) – неравенство (2).
Доказать. Неравенства (1) и (2) равносильные.
Доказательство. Пусть при х = а P(a) > Q(a) – верное числовое неравенство, т.е.
х = а – одно из решении первого неравенства. T(a) – значение Т(х) при х = а Т(а) > 0.
По свойству числовых неравенств P(a)(T(a) > Q(a)(T(a) – тоже верное числовое неравенство, т.е. х = а –одно из решении первого неравенства. Следовательно, если
|
|
|
х= а – решение первого неравенства, то х = а – также решение второго неравенства.
Пусть при х = b неравенство P(b)(T(b) > Q(b)(T(b) – верное числовое неравенство, т.е. х = b – одно из решении второго неравенства. По свойству числовых неравенств P(b) > Q(b) – тоже верное числовое неравенство, так как T(b) > 0. Следовательно,
х = b – одно из решении первого неравенства.
Поскольку множества решении первого и второго неравенств совпадают, то они равносильные.
Теорема4. Если обе части неравенства умножить на одно и то же отрицательное число или на одно и то же выражение, отрицательное при всех значениях переменной, и изменить знак неравенства на противоположный, то получим неравенство, равносильное данному.
Эта теорема доказывается аналогично 3.
Дата добавления: 2018-05-13; просмотров: 846; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
