Влияние безработицы на ВВП. Корреляционно-регрессионный анализ динамики

⇐ ПредыдущаяСтр 7 из 9Следующая ⇒

Как уже упоминалось выше, безработица непосредственно влияет на ВВП. Чтобы установить взаимосвязь и влияние нескольких факторов на результативный фактор используется множественный корреляционно-регрессионный анализ.

Предположим наличие линейной зависимости между исследуемыми факторами. Построим расчетную таблицу для определения параметров линейного уравнения регрессии:

Таблица 10

Год	Условный год ,(t)	Численность безработных, млн.чел, (X1t)	Индекс потребительских цен в %, (Х2t)	ВВП, млрд. руб, (Y_t)
2002	1	6,2	115,1	10830,5
2003	2	5,7	112	13243,2
2004	3	5,8	111,7	17048,1
2005	4	5,2	110,9	21625,4
2006	5	5,0	109	26903,5
2007	6	4,2	111,9	33258,1
2008	7	5,3	113,3	41444,7
2009	8	6,4	108,8	38786,4
2010	9	5,6	108,8	44939,2
2011	10	5,0	106,1	47137,8
Итого:	55	54,4	1107,6	295216,9

Источник: Составлено автором по данным Федеральной службы государственной статистики

Определим тренды ( 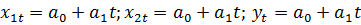) Для этого построим графики динамики безработицы, индекса потребительских цен и ВВП во времени.

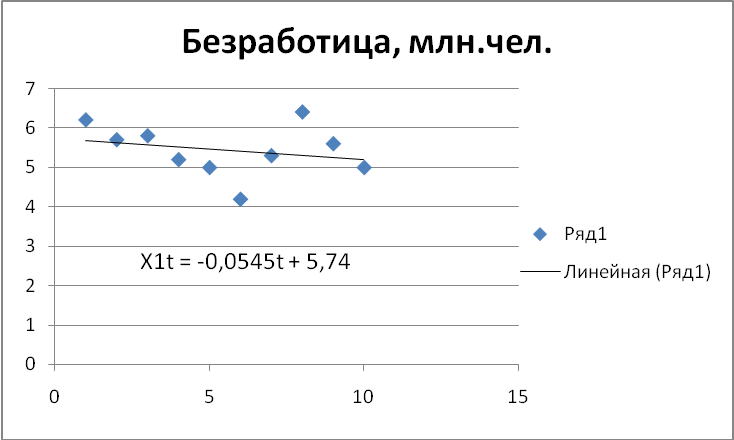
Рис.5

Источник: Составлено автором

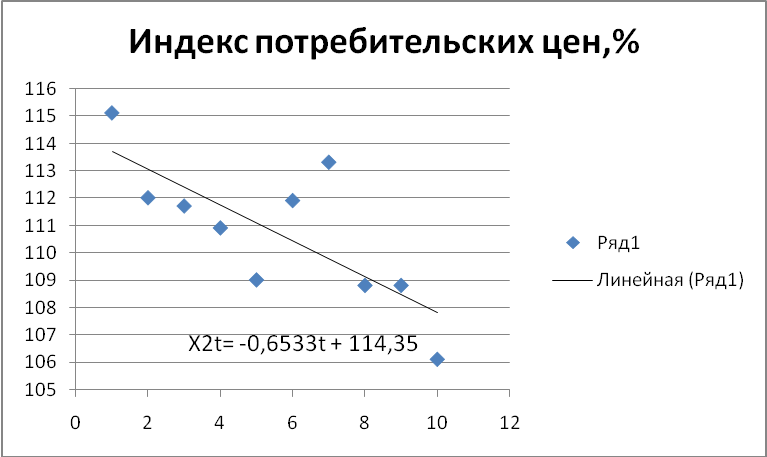
Рис.6

Источник: составлено автором

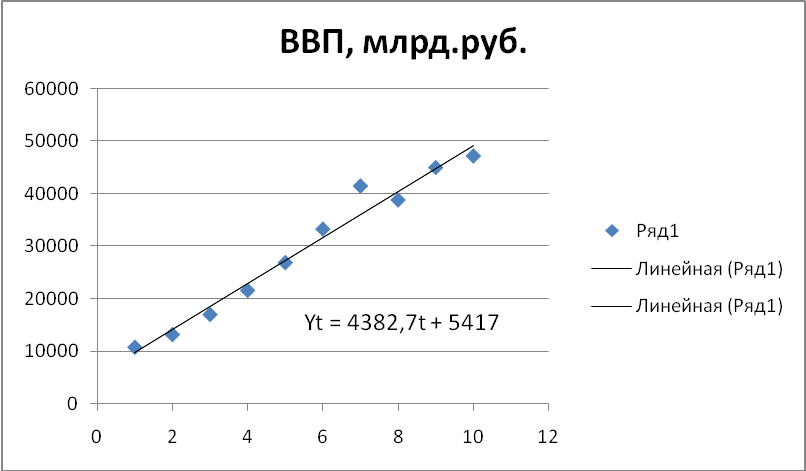
Рис.7

Источник: составлено автором

Из графиков получим уравнения трендов: x₁_t= -0,0545t+5,74;

x₂_t= -0,6533t+114,35; у_t=4382,7t +5417. После расчетных значений y_t, x₁_t и x₂_t находятся отклонения от тренда, рассчитанные по формулам: ε_t = x_it – x_it₍_t_)ср.и γ_t = y_it - y_it₍_t_)ср.

Таблица 11

Год	Условный год ,(t)	X₁t(t)ср	X₂t(t)ср	Y_t(t)ср.
2002	1	5,6855	113,6967	9799,7
2003	2	5,631	113,0434	14182,4
2004	3	5,5765	112,3901	18565,1
2005	4	5,522	111,7368	22947,8
2006	5	5,4675	111,0835	27330,5
2007	6	5,413	110,4502	31713,2
2008	7	5,3585	109,7769	36095,9
2009	8	5,304	109,1236	40478,6
2010	9	5,2495	108,4703	44861,3
2011	10	5,195	107,817	49244
Итого	55	54,4025	1107,569	295218,5

Таблица 12

Год	Условный год ,(t)	ε_1t	ε_2t	γ_t	ξ²_1t	ξ²_2t	γ_t²
2002	1	0,5145	1,4033	1030,8	0,26471	1,9692509	1062549
2003	2	0,069	-1,0434	-939,2	0,004761	1,0886836	882096,6
2004	3	0,2235	-0,6901	-1517	0,049952	0,476238	2301289
2005	4	-0,322	-0,8368	-1322,4	0,103684	0,7002342	1748742
2006	5	-0,4675	-2,0835	-427	0,218556	4,3409723	182329
2007	6	-1,213	1,4698	1544,9	1,471369	2,160312	2386716
2008	7	-0,0585	3,5231	5348,8	0,003422	12,412234	28609661
2009	8	1,096	-0,3236	-1692,2	1,201216	0,104717	2863541
2010	9	0,3505	0,3297	77,9	0,12285	0,1087021	6068,41
2011	10	-0,195	-1,717	-2106,2	0,038025	2,948089	4436078
Итого	55	-0,0025	0,0315	-1,6	3,478546	26,309433	44479070

Источник: Составлено автором

Таблица 13

Год	Условный год ,(t)	ξ1t* ξ2t	γ_tξ_1t	γ_tξ2_t	γ_t¹	(у_t-γ_t^{1)^2}	^γ2_t	(у_t-γ_t²)^{^2}
2002	1	0,72199785	530,3466	1446,52164	9799,7	1062546,447	9883,24008	897301,3481
2003	2	-0,0719946	-64,8048	979,96128	14182,4	882102,5513	14349,5325	1223971,531
2004	3	-0,15423735	-339,0495	1046,8817	18565,1	2301304,869	18815,8249	3124851,154
2005	4	0,2694496	425,8128	1106,58432	22947,8	1748761,104	23282,1172	2744712,003
2006	5	0,97403625	199,6225	889,6545	27330,5	182337,0256	27748,4096	713872,2677
2007	6	-1,7828674	-1873,964	2270,69402	31713,2	2386680,536	32214,702	1088679,376
2008	7	-0,20610135	-312,9048	18844,35728	36095,9	28609516,33	36680,9944	22692891,14
2009	8	-0,3546656	-1854,651	547,59592	40478,6	2863593,799	41147,2868	5573786,358
2010	9	0,11555985	27,30395	25,68363	44861,3	6065,647747	45613,5792	454787,2485
2011	10	0,334815	410,709	3616,3454	49244	4436161,909	50079,8715	8655784,958
Итого	55	-0,15400775	-2851,579	30774,27969	295219	44479070,22	299815,558	47170637,39

По исходным данным и отклонениям находим парные коэффициенты корреляции по формулам: r_γtξt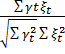₌ и r_ε1_t_ξ2_t = 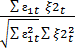. Получим:

r_γtξ₁_t = -0,22925; r_γtξ₂_t₌0,8996101 и r_ε1_t_ξ2_t =-0,016099. Коэффициенты корреляции нужно занести в таблицу:

Таблица 14

Независимая переменная	Коэфф.корреляции
Независимая переменная	ξ1t	ξ2t	между аргументом и функцией
ξ1t	1	-0,0161	-0,22925
ξ2t	-0,0161	1	0,89961

Величина данных коэффициентов показывает наличие взаимодействия факторных показателей на результативный,т.е. Х₁ и Х₂ на У.

После отбора факторов строится уравнение по методу последовательного включения переменных в уравнение регрессии. Сначала необходимо построить уравнение для зависимости y_t= f (x₁_t). Построение уравнения осуществляется по методу исключения тенденции. Уравнение с двумя факторными переменными в стандартизированной форме имеет вид:

Т_γ= β₁+β₂. Для определения β-коэффициентов используют систему уравнений:

r_γt ₁_t ₌β1_* r_ε1_t_ε1_t ₊β2_* r_ε1_t_ε₂_t

r_γt ₂_t=β1*r_ε1_t_ε2_t₊β2*r_ε2_t_ε₂_t

Решив систему уравнений, получили β1=-0,2146, а β2= 0,895.

Т.е. уравнение Тγ= -0,2146Т1+0,895 Т2. После преобразований уравнение регрессии примет вид: 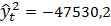-766,96*х₁_t+501,526*x₂_t+4752,14*t.

Для определения тесноты множественной связи используется специальный показатель- коэффициент множественной корреляции R, который определяется по формуле: R= 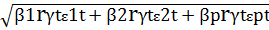. Так, для данной модели R=0, 924475. Следовательно R²=0,854654.

Найдем частные коэффициенты детерминации, которые показывают вклад каждого фактора в изменение эндогенной переменной. Так, d₁= 0,0492; d2=0,8054. Таким образом, совместное воздействие первого и второго аргументов обеспечивает 85,47% общей вариации показателей.

Несмотря на значение R, оно может быть завышено, т.к.количество наблюдений невелико. Поэтому чтобы оценить общую вариацию результативного признака в зависимости от факторных, величина R корректируется на основании следующей формулы: R’= 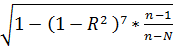, где N- количество факторных признаков. Получается,что R’= 0,999.

Проверка статистической значимости коэффициента множественной корреляции R производится на осонове F-критерия Фишера по формуле: F= 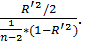Подставив известные значения в формулу, получаем F_набл.=2594678,4. Далее нужно сравнить полученное значение F_набл.с табличным значением F_крит. при уровне значимости p=0,95 и числом степеней свободы k1=2 и k2=n-2=8. Получается F_крит.=4,46. Так как F_набл.>F_крит.,то коэффициент множественной корреляции R признается значимым.

Кроме того, следует определить доверительные интревалы для R. Так как p=0,95, то по нормальному закону распределения величина t=1,96. Необходимо посчитать значение t*σ_R. σ_R находится как 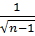,т.е. в рассматриваемом примере σ_R =0,333. Отсюда t*σ_R =0,6533. По таблице z-преобразования Фишера для R=0,999 z= 3,8002. Таким образом:

3,8002-0,6533< z₀ <3,8002+0,6533. Для z_ниж.=3,1469 R_ниж.=0,996z, а для z_вер.=4,4535 R_вер.=1. Таким образом, статистическая значимсоть коэффициента корреляции при вероятности 95% будет сохраняться в пределах от 0,996 до 1.

Проверка адекватности уравнения регрессии включает проверку значимости каждого коэффициента на основе t-критерия Стьюдента:

t_p= 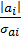, где σ²_ai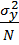₌ _{= 3369331,2.}Вычислив корень из σ²_ai , σ_ai будет равна 1835,5738.

Подставив значения a_i и σ_ai в формулу, получаются значения t^a¹_p =0,418, а t^a²_p=0,273. Табличное значение t при уровне значимости p=0,95 и числом степеней свободы= 7 будет равно 2,3646. Таким образом, t_1наб.и t_2наб.<t_крит.,и можно сделать вывод, что первый коэффициент с вероятностью, меньшей 50%, более значим, чем второй коэффициент.

Сравнивая результаты расчетов можно отметить, что модель адекватна по критерию Фишера. Однако коэффициенты уравнения регрессии, проверенные по t-критерию Стьюдента, недостаточно значимы, и в этом случае модель пригодна для принятия некоторых решений, но не для прогнозов.

Таким образом, основываясь на данных проведенного анализа, можно утверждать, что численность безработных в стране оказывает влияние на размер ВВП в большей степени,чем индекс потребительских цен. Однако для более точного анализа необходимо включение других факторных признаков.

ЗАКЛЮЧЕНИЕ.

Дата добавления: 2018-05-13; просмотров: 625; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 678 9 Следующая ⇒

Мы поможем в написании ваших работ!