Обобщение схемы независимых испытаний. Локальная теорема Муавра – Лапласа.

1. Пусть производится n независимых опытов, в каждом из которых может появиться или не появиться некоторое событие А, причем вероятность появления события А в i-м опыте равна p_i, а вероятность непоявления qi=1 – pi(i= 1...n). Требуется найти вероятность Р_m,n того, что в результате n опытов событие А появится ровно m раз.

Вероятность того, что событие А в n независимых опытах появится ровно m раз, равна коэффициенту при x^m в выражении производящей функции:

где p_i — вероятность появления события А в i-м опыте, q_i = 1 – p_i

 

2.Пусть производится n независимых опытов, в каждом из которых событие

А₁ появится m₁раз с вероятностью p₁

А₂ появится m₂ раз с вероятностью p₂

_{......................}

А_k появится m_k раз с вероятностью p_k

И 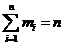 . Требуется найти вероятность Рn,m₁m₂,...,m_k того, что в результате n опытов событие А_i появится ровно m_i раз.

Такая вероятность равна коэффициенту при 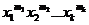 в выражении производящей функции:

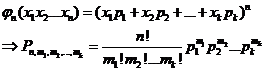
Локальная теорема Муавра – Лапласа.

Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина 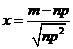  ограничена равномерно по m и n 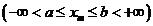, то

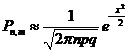
Эта формула работает плохо при малых р, а хорошо при р = q

 

Теорема Бернулли, как одна из форм закона больших чисел.

Теорема Бернулли устанавливает связь между относительной частотой появления события и его вероятностью.

Если m число появления события А в n независимых испытаниях с вероятностью успеха в одном испытании p, 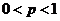, то для любого 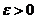справедливо .

                                                  

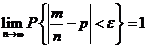
Это означает, что с ростом числа испытаний n относительная частота успехов 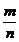 приближается к вероятности p успеха в одном испытании.

Задача 13.1 (а,б).

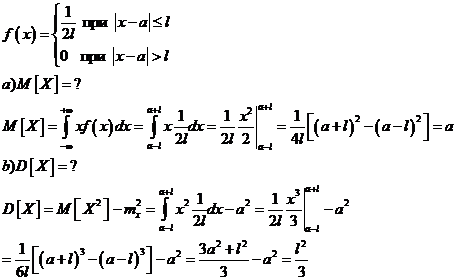
Экзаменационный Билет №10

Функции распределения случайных величин.

Функцией распределения случайной величины X называется функция F(х), выражающая вероятность того, что X примет значение, меньшее чем х:

F(x) = P(X <x).

Функция F (х) есть неубывающая функция;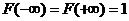

Для дискретных случайных величин функция распределения есть разрывная ступенчатая функция, непрерывная слева.

Если функция распределения F (х) везде непрерывна и имеет производную, случайная величина называется непрерывной в узком смысле слова или просто непрерывной.

Если функция распределения F (х) на некоторых участках непрерывна, а в отдельных точках имеет разрывы, случайная величина называется смешанной.

Закон больших чисел в форме теоремы Чебышева.

Пусть  папарны независимых случайных величин, имеющих математическое ожидание М[X­_i] и дисперцию, ограниченную некоторую постоянную величину с, .

При достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию.

 

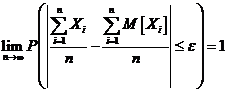
Доказательство

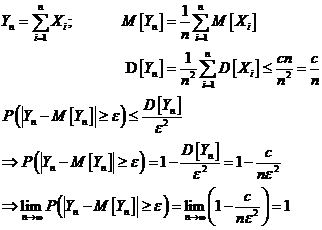
Задача 10.3.

X_i – случайное число испытания приборов.

X₁ = 1; X₂ = 2; X₃ = 3; X₄ = 4; X₅ = 5

Потому, что каждый следующий прибор испытается только в том случае, если предыдущий оказал надёжным, вероятность Р_i = P(X = x_i) вычисляется по формуле:

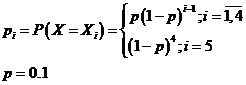
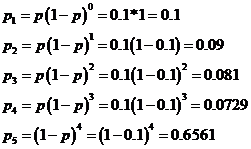
Xi	1	2	3	4	5
pi	0.1	0.09	0.081	0.0729	0.6561

Экзаменационный Билет №11

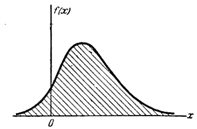1. Плотность распределения случайных величин.

Плотностью распределения непрерывной (в узком смысле слова) случайной величины называется функция f(x) = F'(x).

Плотность распределения любой случайной величины неотрицательна, f(x) > 0, и обладает свойством

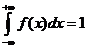
График плотности f(x) называется кривой распределения.

Элементом вероятности для случайной величины X называется величина f(x)dx, приближенно выражающая вероятность попадания случайной точки X в элементарный отрезок dx, примыкающий к точке х.

Функция распределения F (х) выражается через плотность распределения формулой

Вероятностьпопадания случайной величины X на участок от 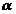 до 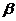(включая 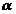) выражается формулой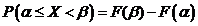

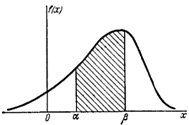Если случайная величина X непрерывна, то 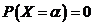и

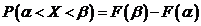
Вероятность попадания на участок от 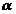 до 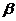 для непрерывной случайной величины выражается формулой

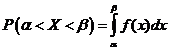
Неравенство Чебышева.

Первая формула.

Если х – случайная неотрицательная велична, то

Доказательство:

1.Пусть величина X прерывная, с рядом распределения

xi	x1	x2	...	xn
p1	p1	p2	...	pn

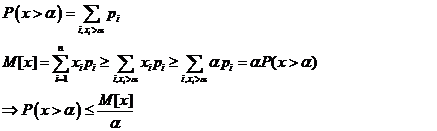
2. Для непрерывных величин

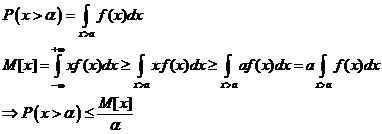
B. Вторая формула.

Пусть имеется случайная величина X с математическим ожиданием m_x и дисперсией D_x. Неравенство Чебышева утверждает, что каково бы ни было положительное число а, вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на 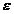  , ограничена сверху величиной : .

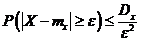Доказательство:

1.Пусть величина X прерывная, с рядом распределения 

xi	x1	x2	...	xn
p1	p1	p2	...	pn

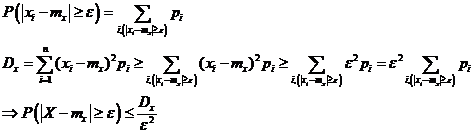
2. Для непрерывных величин

 

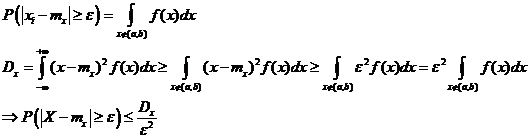
Примечание.

Неравенство Чебышева дает только верхнюю границу вероятности данного отклонения. Выше этой границы вероятность не может быть ни при каком законе распределения. На практике в большинстве случаев вероятность того, что величина X выйдет за пределы участка 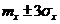значительно меньше ¹/₉

Задача 12.3.

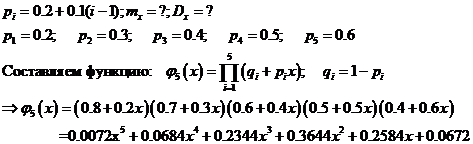
Мы имеем ряд распределения:

Xi	0	1	2	3	4	5
Pi	0.0672	0.2584	0.3644	0.2344	0.0784	0.0072

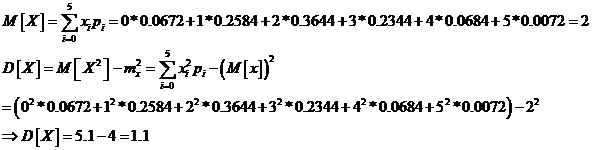
Экзаменационный Билет №12

---

Дата добавления: 2018-05-13; просмотров: 241; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

⇐ Предыдущая12345678910Следующая ⇒

---

Мы поможем в написании ваших работ!