Кинематический анализ рычажных механизмов

Постановка задачи

Если число степеней свободы механизма W = 1, то при фиксированных размерах звеньев значения их кинематических параметров движения однозначно определяются значениями кинематических параметров движения одного звена, называемого входным, которым и считается то звено, характер движения которого при кинематическом анализе полагается известным.

Тогда задача кинематического анализа формулируется следующим образом: при известных мгновенных значениях кинематических параметров движения входного звена определить мгновенные значения кинематических параметров движения остальных звеньев.

Таким образом, задача кинематического анализа решается автономно в каждом положении механизма, а для полного кинематического исследования её надо решить многократно для ряда последовательных положений механизма за весь цикл его работы.

В дальнейшем при нумерации звеньев входное всегда будет иметь номер 1. Если оно совершает вращательное движение, то по условию задачи должны быть заданы: его угол поворота j₀₁ от оси Х₀ неподвижной системы координат (НСК), угловая скорость w₁, угловое ускорение e₁. Если вращающееся входное звено совершает полные обороты, то его называют кривошипом. Часто его угол поворота удобно отсчитывать от того значения j₀₁, которое соответствует какому-то характерному положению механизма, например, крайнему положению рабочего органа, тогда будем обозначать его j₁.

В результате решения задачи для звеньев, совершающих сложное движение, например, шатуны, необходимо определить:

а) поступательную составляющую движения, характеризуемую положением, скоростью и ускорением центра масс,

б) вращательную составляющую, характеризуемую углом поворота, угловой скоростью и угловым ускорением звена. Для вращающихся звеньев достаточно определить их угол поворота, угловую скорость и угловое ускорение. Для поступательно движущихся звеньев – положение интересующей нас точки, например, центра масс и его линейную скорость и ускорение.

Решение описанной задачи опирается на структурный анализ механизма. Общая последовательность кинематического расчета следующая.

1. По исходно заданным кинематическим параметрам движения входного звена определяются параметры движения той его точки, в которой присоединяется первая структурная группа. Эти значения преобразуются в её систему координат.

2. Производятся расчеты для этой структурной группы и вычисляются параметры движения той точки её звена, в которой присоединяется следующая группа.

3. Эти значения преобразуются в систему координат следующей структурной группы, производится её расчет и т.д.

В соответствии с описанным алгоритмом строится и дальнейшее изложение. Сначала будет рассмотрена кинематика входных механизмов, а после этого расчет структурных групп, для которых уже можно будет полагать, что параметры движения входных кинематических пар известны. Основные расчетные зависимости для структурных групп получим методом векторных контуров [5, 9, 14, 18], параметры движения характерных точек на звеньях, таких как центры масс, рабочий орган и т.п. – методом преобразования координат.

Расчетные зависимости для определения кинематических параметров движения звеньев будут получены для структурных групп 2 класса 2 порядка. При этом итоговые выражения в качестве необходимых исходных данных будут содержать параметры движения входных кинематических пар. Это позволяет использовать полученные зависимости для расчета механизмов, содержащих несколько структурных групп и при различных видах движения входного звена.

 

2.1.1. Метод планов скоростей и планов ускорений

 

Скорости и ускорения могут быть определены с помощью графических построений, которые называются соответствующими планами.

Из теоретической механики известно, что движение некоторой точки М по отношению к основной системе отсчета, которая принята за неподвижную, называется абсолютным, по отношению к подвижной системе отсчета - относительным, а движение подвижной системы отсчета по отношению к основной - переносным движением. 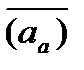Скорость и ускорение точки М по отношению к каждой из систем называют соответственно абсолютными скоростью  и ускорением  или относительными скоростью  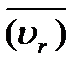и ускорением 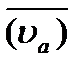. Скорость и ускорение точки М', связанной с подвиж­ной системой отсчета и совпадающей в данный момент с дви­жущейся точкой М, называют переносной скоростью  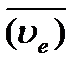и ускорением .

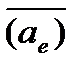Абсолютные скорость и ускорение любой точки можно найти из векторных уравнений вида

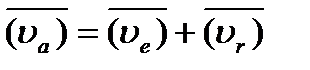,	(2.7)
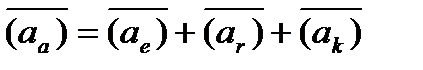.	(2.8)

 

В общем случае переносное и относительное ускорения состоят из нормальной (центростремительной) и тангенциальной (касательной) составляющих

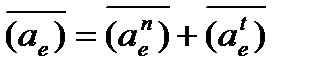,	(2.9)
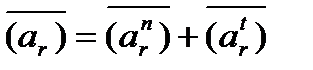.	(2.10)

Кориолисово (поворотное) ускорение определяется равенством

,

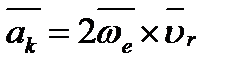(2.11)

а его величина равна:

,

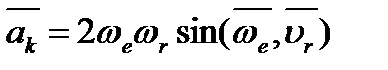(2.12)

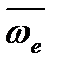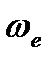где  и  - вектор и величина переносной угловой скорости. Из выражений (2.11) и (2.12) следует, что  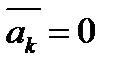в трех случаях: когда переносное движение является поступательным ( 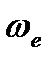=0), когда точка имеет мгновенную остановку в относительном движении (u_r = 0), когда векторы  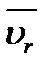и 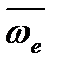 параллельны (sin( 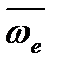, 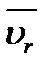) = 0).

Методы планов скоростей и ускорений позволяют с помощью графических построений решать системы уравнений типа (2.7) и (2.8). Покажем это на двух простых примерах.

Рассмотрим структурную группу 1-го вида (рис. 2.6, а), для точек В и D которой известны скорост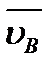и  и 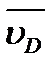, а также ускорения 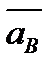и 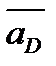. Нужно определить скорости и ускорения точек С, S₂ и S₃. В неподвижной системе отсчета точки С₂ и С₂ звеньев 2 и 3 движутся одинаково, постоянно совпадая с центром шарнира С. Расстояния ВС₂= ВС и DC₃=DC при этом не изменяются.

Подставляя в выражение (2.7) для звена 2 , 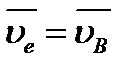и 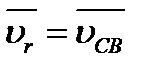, а для звена 3 - 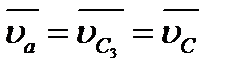, , 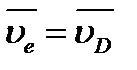, 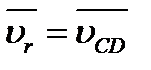получаем систему уравнений

      

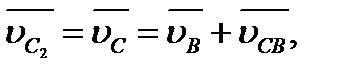
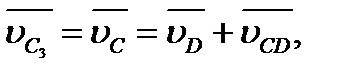
в которых известны 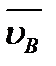 и 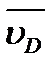, а неизвестны величина и направление 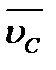, а также величины векторов  и 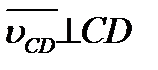. Такую систему уравнений можно решить графически.

Для этого из произвольной точки Р_v, названной полюсом плана скоростей, откладываем в удобном масштабе векторы 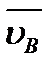 и 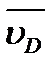, а через их концы b и d проводим прямые, параллельные относительным скоростям  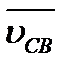и 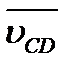, т. е. перпендикулярные отрезкам СВ и CD (рис. 2.6, б). Точка с пересечения этих прямых будет являться концом вектора 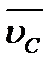, начало которого лежит в полюсе плана Р_v. Относительные скорост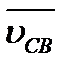и  и 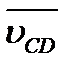 будут представлены векторам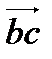и  и .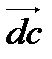

 

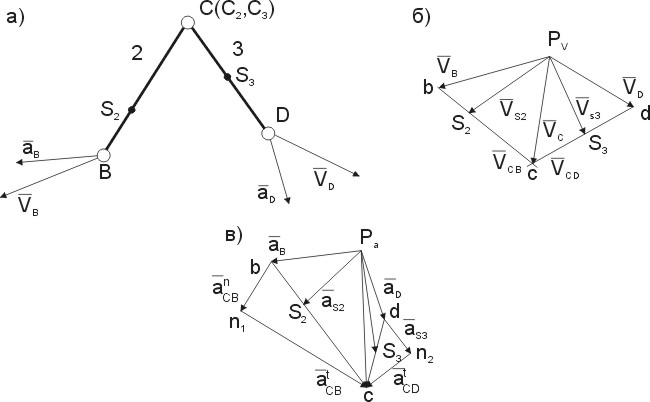
Рис. 2.6

 

Планом скоростей звена называют геометрическое место концов векторов скоростей всех точек этого звена (каждый вектор начинается в полюсе Р_v).

Для нахождения скоросте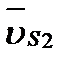й  и 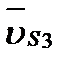, точек S₂ и S₃ удобно воспользоваться так называемым правилом подобия: план скоростей звена подобен самому звену и повернут по отношению к нему на угол 90°. Поэтому концы S₂ и S₃ векторов  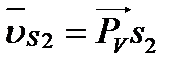и 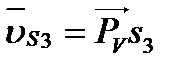 можно определить делением отрезков bc и cd в соответствии с пропорциям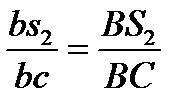и

и .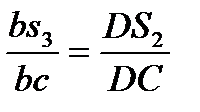

(2.13)

Величины всех найденных скоростей находятся с учетом принятого масштаба. Вся совокупность построений называется планом скоростей группы.

В данном случае переносное движение является поступательным ( 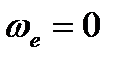), поскольку звенья 2 и 3 образуют друг с другом вращательную пару и поворот одного звена не вызывает поворота другого. Для определения ускорения точки С используем выражение (2.8), а с учетом  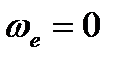и 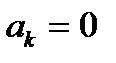 получим такую систему уравнений:

;  ,

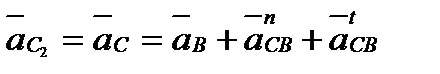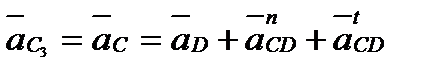(2.14)

где 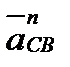 и 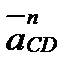 - нормальные (центростремительные) составляющие относительных ускорений, направленные параллельно СВ и CD от точки С в сторону точек В и D;
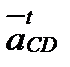   и  - тангенциальные (вращательные) составляющие относительных ускорений, направленные перпендикулярно отрезкам ВС и CD.

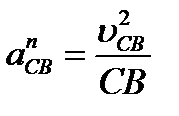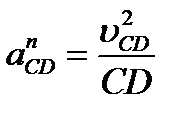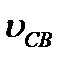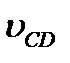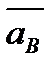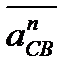Величины нормальных составляющих определяют с помощью выражений  и , в которые подставляются  и , найденные из плана скоростей. После определения нормальных составляющих систему (2.14) можно решить графически. Для этого из произвольно взятой точки Р_а - полюса плана ускорений - откладываем в удобном масштабе векторы  и , затем пристраиваем в точках b и d векторы  и 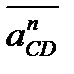, а через концы n₁ и n₂ последних проводим прямые, параллельные  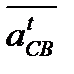и 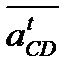 (рис. 2.6, в). 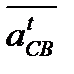Точка пересечения с этих прямых и будет являться концом вектора , начало которого лежит в полюсе плана Р_а, а также концом каждого из векторов  и 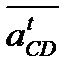,начинающихся в точках n₁ и n₂.

Для нахождения ускорени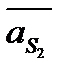й  и 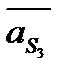 снова воспользуемся правилом подобия: план ускорений звена подобен самому звену и повернут по отношению к нему на угол 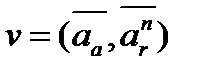. Поэтому для построения точек s₂ и s₃ остаются справедливыми пропорции (2.13). Эти точки находят после проведения отрезков bc и dc. Вся совокупность выполненных построений называется планом ускорений группы.

Теперь на примере структурной группы 3-го вида (рис. 2.7, а) рассмотрим более общий случай. Звенья 2 и 3такой группы образуют друг с другом поступательную пару, и поворот одного из них влечет за собой поворот другого. Кроме того, совпадающие в данный момент с точкой С точки С₂, и С₃ движутся по-разному, т. е. имеют различные скорости и ускорения. Расхождение точек C₂ и С₃ по прямой будем считать относительным движением, а вращение звеньев группы с угловой скоростью 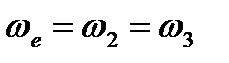 - переносным.

 К точке В потребуется подойти так же, как и к точке С, т. е. считать, что в точке В помимо реальной точки В₂, принадлежащей звену 2, находится воображаемая точка В₃, принадлежащая звену 3.

Для простоты положим, что звено 3 вращается вокруг неподвижной точки D, т. е.  и 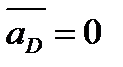, с известной в данный момент угловой скоростью w₃. Заданными будем считать скорость  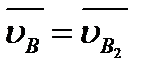и ускорение  точки В на звене 2.Определению подлежат скорости и ускорения точек B₃, C₂, C₃, S₂, и S₃.

Сначала определим 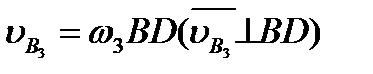 и . Затем с учетом формулы (2.10) составим систему уравнений 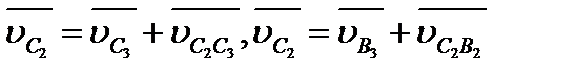, в которых известны направления векторов 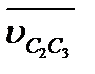||CD и 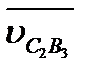^BC.

Отложив в удобном масштабе из выбранного полюса Р_v векторы 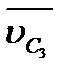 и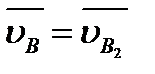  
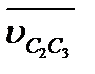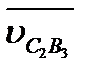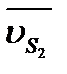(рис. 2.7, б) и проведя через их концы c₃ и b₂ прямые, параллельные ||CD и ^BC, находим точку их пересечения c₂, являющуюся концом вектора . Для нахождения точек s₂ и s₃ и векторов  и 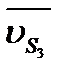 снова используем правило подобия и отношения (2.13), в которых b нужно заменить на b₂, а с - на c₂ или c₃ и учесть, что точка d совпадает с полюсом Р_v.

Помимо этого на плане скоростей группы нужно изобразить уже известный вектор 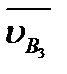 и найти относительную скорость 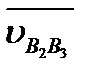||CD, которая потребуется в дальнейшем. Если все построения верны, то в соответствии с правилом подобия Ddb₃c₃ ~ DDBC.

 

Рис. 2.7

 

Для определения ускорений используем формулы (2.8) - (2.10), которые позволяют получить необходимые системы уравнений. Так, для точки В₂ 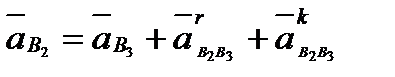; 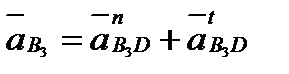, где  и .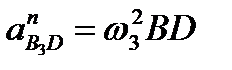

Отложив из полюса Р_а в удобном масштабе известные векторы 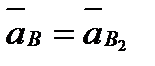 и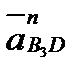  
(рис. 2.7, в), пристраиваем концом к точке b₂ вектор 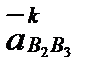, через его начало проводим прямую, параллельную 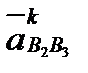||CD, а через конец вектора  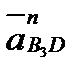- точку п - прямую, параллельную 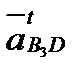. Пересечение этих прямых дает нам точку b₃ - конец вектора .

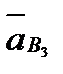Для нахождения ускорения 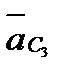 точки С₃ используем правило подобия, построив на отрезке db₃ (здесь точка d совпадает с полюсом плана Р_а) как на стороне и двум примыкающим к ней углам треугольник db₃c₃, подобный треугольнику DBC.

Теперь можно решить такую систему уравнений:

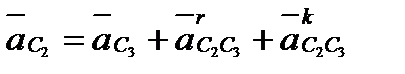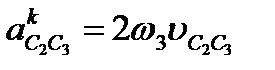; , где и .

Отложив из найденной предыдущим построением точки С₃ вектор 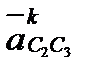, проведем через его конец прямую, параллельную 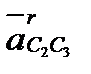||CD. Затем, отложив из точки b₂ вектор ||ВС, проведем через его конец прямую, параллельную 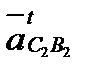(^ВС). Пересечение указанных прямых дает нам точку С₂ - конец вектора 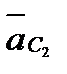. Точки s₂ и s₃, определяющие концы векторов  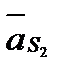и 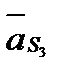, находим по правилу подобия пропорциональным делением отрезков b₂c₂ и c₃d.

 

2.1.2. Метод векторных контуров

 

Этот аналитический метод удобен для нахождения угловых кинематических параметров с помощью системы уравнений, полученных из условия замкнутости одного или нескольких векторных контуров, которые определяют положение звеньев механизма. Например, шарнирный четырехзвенник (рис. 2.8) можно представить всего одним векторным контуром .

 

 

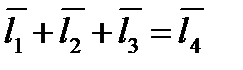Рис. 2.8

 

Проецируя его на оси ОХ и OY неподвижной системы координат, получаем

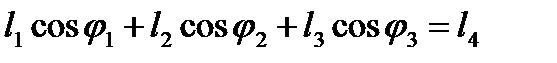,	(2.15)
.

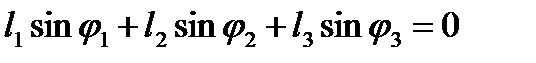Величины l₁, l₂, l₃, l₄, и j₁ считаем заданными. Тогда система (2.15) относительно j₂ и j₃ может быть решена, например, следующим образом. Записав

;

                             ,

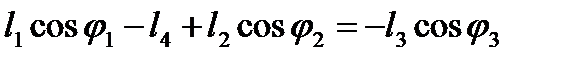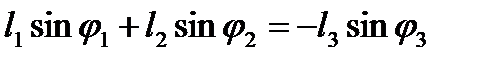или	,	(2.16)
	,

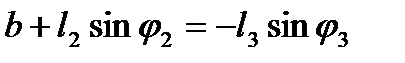где 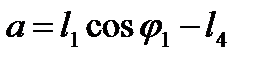 и .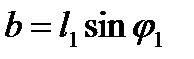

Возведем уравнения (2.16) в квадрат и сложим, в результате получим

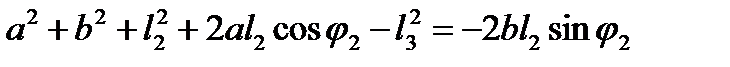
или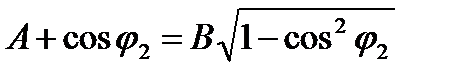

,

(2.17)

где 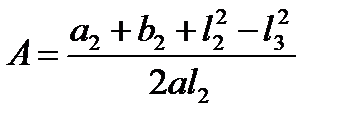 и .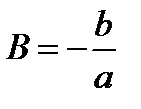

После возведения в квадрат обеих частей выражения (2.17) получаем следующее квадратное уравнение для определения угла j₂:

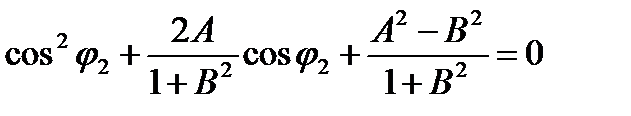
(его решение для краткости не приводим).

Определив угол j₂, находим j₃, использовав любое из уравнений (2.16).

Угловые скорости ω₂ и ω₃ звеньев 2 и 3 найдутся после дифференцирования уравнений (2.15) по времени. Учитывая, что dj₁/dt=ω₁ (эта угловая скорость считается заданной), dj₂/dt= ω₂ и dj₃/dt= ω₃, а l₄ = const, получаем систему

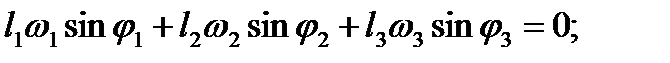
	(2.18)

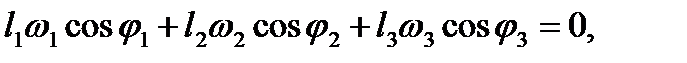
которую можно решить приемом вычитания одинакового известного угла j₂ или j₃ из всех углов, входящих в первое уравнение. Так, вычитая j₃, получаем 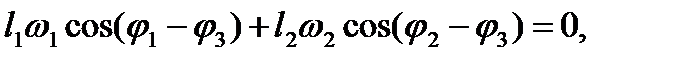 откуда

.

,

,

Для нахождения угловых ускорений e₂=dw₂/dt и e₃=dw₃/dt дифференцируем по времени уравнения (2.18), полагая w₁ = const и e₁ = 0. В результате имеем

.

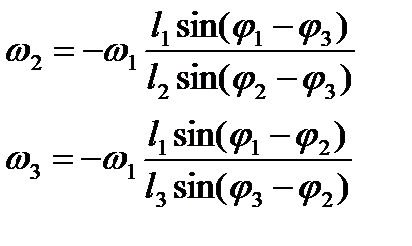
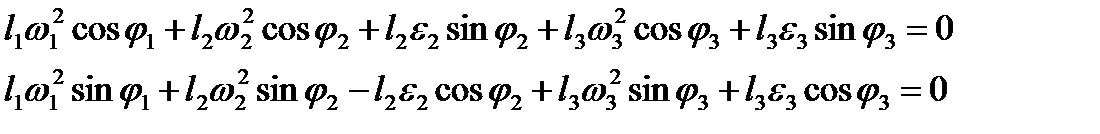
Используя тот же прием, что и для решения системы (2.18), находим

.

,

 

 

---

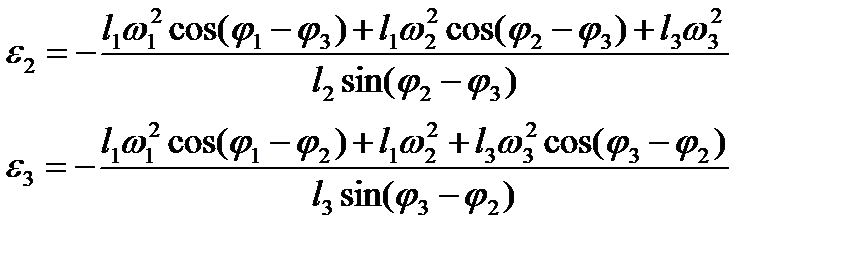
Дата добавления: 2018-05-12; просмотров: 323; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!