Закон сохранения заряда. Уравнение непрерывности
В данном вопросе рассматривается фундаментальное свойство электрических зарядов – принцип их локального сохранения, вводится уравнение непрерывности.
Из 1-го и 3-го уравнения Максвелла следует важный вывод, на котором хотелось бы остановиться поподробнее. Возьмем 1-е уравнение Максвелла:
.
Далее берем операцию div от обеих частей этого выражения:
.
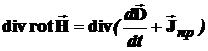Из высшей математики известно, что операция дивергенции ротора какой-либо векторной величины тождественна равна нулю, тогда:
,
или 
,
или 
.
Используя 3-е уравнение Максвелла 
, получаем:
.
Проинтегрируем по объему V обе части уравнения:
.
Применим к левой части теорему Остроградского-Гаусса, тогда:
,
или окончательно:
. (28)
где: Iпр – ток, пересекающий замкнутую поверхность S, ограничивающую объем V, в котором находится заряд Q.
Полученное выражение (28) выражает закон сохранения заряда:
электрический ток I, выходящий за некоторый промежуток времени через замкнутую поверхность S, ограничивающую объем V, равен величине уменьшения находящегося в объеме заряда Q за тот же промежуток времени.
Закон сохранения заряда устанавливает, что заряд не может переместится из одной точки в другую не создав между ними тока. С другой стороны, если не происходит изменение заряда в объеме V, то ток проводимости равен нулю. Это означает в свою очередь, что:
|
|
|
- либо ток вообще отсутствует;
- либо распределение зарядов по всему объему проводника остается неизменным во времени, т.е. количество зарядов поступивших за некоторый промежуток времени в замкнутый объем, в точности равно количеству зарядов, вытекающих за тот же промежуток времени из этого объема. Очевидно, что это имеет место в случае постоянного электрического тока. Поэтому для постоянного электрического тока получаем:
. (29)
Данное уравнение носит название уравнения непрерывности постоянного токав интегральной форме.
Из него следует (сравните, например, с 4-м уравнением Максвелла), что силовые линии плотности постоянного тока проводимости непрерывны, т.е. образуют замкнутые линии, и ток через любую замкнутую поверхность равен нулю.
Полная система уравнений электродинамики. Уравнения Максвелла в комплексной форме
В этом вопросе обобщается физический смысл уравнений Максвелла, формулируются уравнения Максвелла для гармонических полей.
Сведем вместе основные уравнения макроскопической электродинамики, с помощью которых можно описать все многообразие свойств электромагнитных явлений. Эти уравнения, как показано в первых трех вопросах лекции, могут быть записаны либо в интегральной форме, либо в дифференциальной форме.
|
|
|
Интегральная форма записи уравнений устанавливает связь между величинами в разных пространственно разнесенных точках поля или на разных отрезках (поверхностях). Дифференциальная форма описывает соотношение между величинами вблизи одной и той же точки поля в определенный момент времени. Чаще всего именно это форма записи уравнений Максвелла используется на практике при исследовании электромагнитных полей, изменяющихся от точки к точке.
Запишем уравнения Максвелла в виде системы:
В дифференциальной форме: В интегральной форме:
1. rot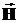 
= 
1. 
= 
2. rot 
= - 
(30) 2. 
= - 
(31)
3. div 
= ρ 3. 
4. div 
= 0 4. 
Полная система уравнений электродинамики включает в себя: приведенные выше 4-ре уравнения Максвелла и уравнения (их называют материальными уравнениями), которые связывают между собой векторы 
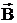и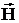 
, 
и 
, 
и .
В случае линейных изотропных сред, материальные уравнения имеют вид:
|
|
|
, 
, 
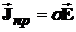. (32)
Эти материальные уравнения показывают, что между величинами, входящими в уравнения Максвелла, существует взаимосвязь: а именно вектор электрической индукции 
связан с вектором напряженности электрического поля 
через значение абсолютной диэлектрическую проницаемость среды, а вектор магнитной индукции 
связан с вектором напряженности магнитного поля 
через значения абсолютной магнитной проницаемости среды. И, наконец, последнее материальное уравнение показывает, что в проводниках существует связь между плотностью тока и напряжённостью электрического поля, в хорошем приближении выражаемая законом Ома.
1-ое и 2-ое уравнения Максвелла считаются основными уравнениями электродинамики, 3-е и 4-е – дополнительными, т.к. они вытекают из первых двух.
Сформулируем основные выводы (физический смысл), следующие из уравнений Максвелла:
1) Всякое изменение во времени электрического или магнитного поля приводит к возникновению соответственно вихревого магнитного или вихревого электрического поля. Независимое существование друг от друга переменных электрических и магнитных полей невозможно, они непрерывно переходят одно в другое.
|
|
|
2) Независимое существование электрических и магнитных полей возможно только в случае статических (неподвижных) зарядов и постоянных магнитов.
3) Источниками электрического поля являются заряды и токи, поэтому электрическое поле может быть как потенциальным (заряды), так и вихревым (токи).
4) Источниками магнитного поля являются движущиеся заряды (токи проводимости) или возмущение электрического поля (ток смещения), поэтому магнитное поле всегда имеет вихревой характер.
5) Силовые линии электрического поля могут иметь истоки и стоки, тогда как силовые линии магнитного поля всегда непрерывны, т.е. замыкаются на себя.
Перейдем к представлению уравнений Максвелла в комплексной форме. Необходимость такого представления связана с тем, что на практике очень часто приходится иметь дело с электромагнитными полями, создаваемыми периодически изменяющимися во времени токами и зарядами.
Любая, переменная во времени, величина может быть представлена рядом Фурье в виде суммы дискретных гармонических колебаний:
. (33)
В случае же монохроматических (“одноцветных”) гармонических колебаний:
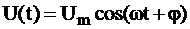. (34)
Величина ω = 2πf = 2π/Τ – называется круговой частотой гармонических колебаний.
Анализ гармонических колебаний значительно упрощается при введении метода комплексных амплитуд («символический метод»). В основу этого метода положена формула Эйлера:
, (35)
тогда гармоническую скалярную величину, например U(t), можно представить как вещественную часть следующей комплексной величины:
, (36)
где: 
- комплексная амплитуда; 
- комплексная скалярная величина.
Рассмотрим теперь представление векторной гармонической величины комплексным вектором.
В общем случае вектор 
, изменяющийся во времени по гармоническому закону в некоторой точке пространства, записывается в виде:
, (37)
где: Аmx,, Amy, Amz – амплитуды отдельных составляющих вектора; φx, φy, φz – их фазовые углы; 
, 
, 
– единичные орты в прямоугольной системе координат.
По сути (37) есть проекция вектора 
на оси прямоугольной системы координат (x, y, z), см. рис. 9.
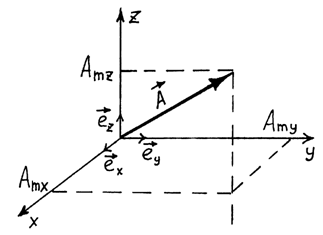
Рис. 9 – Проекции вектора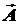 
в прямоугольной системе координат
Представим теперь выражение для вектора (37) через комплексный вектор 
.
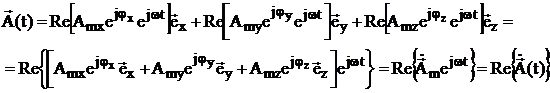, (38)
где: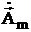 
- комплексная амплитуда вектора, - комплексный вектор
Если комплексный вектор удовлетворяет некоторому линейному дифференциальному уравнению, то это означает, что данному уравнению удовлетворяет как вещественная часть, так и мнимая часть этого комплексного вектора. Поэтому: если требуется найти решение дифференциального уравнения (а уравнения Максвелла как раз такими и являются) в виде комплексного вектора (выражение (37)), то искать его проще, сначала в виде комплексного вектора 
, а затем уже взять от него вещественную часть.
Применим выше изложенное для полученных уравнений Максвелла в комплексной форме. Для этого представим векторы , , , 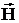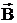и в виде комплексных векторов:
; 
.
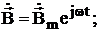
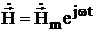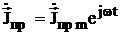Тогда, подставив их в дифференциальную форму уравнений Максвелла (30) получим:
;
; (39)
;
.
Данные уравнения носят название уравнений Максвелла в комплексной форме. В дальнейшем, при использовании системы уравнений (39) индекс m (амплитуды) будем опускать.
Дата добавления: 2018-05-12; просмотров: 2367; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!