Метод наименьших квадратов в случае линейной эмпирической функции
Федеральное государственное образовательное бюджетное учреждение
Высшего образования
«ФИНАН
«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ»
Департамент анализа данных, принятия решений и финансовых технологий
А.В.Потемкин
Метод наименьших квадратов в Excel
Учебно-методические рекомендации для проведения
семинара №19 по компьютерному практикуму
Для бакалавров направления 38.03.01 «Экономика»
Электронное издание
Москва 2017
Метод наименьших квадратов
СОДЕРЖАНИЕ
Введение. 2
1................................................ Основыметода наименьших квадратов. 3
2. Метод наименьших квадратов в случае линейной эмпирической функции 5
3. Непосредственное определение параметров эмпирической линейной функции 7
4. Использование встроенных функций Excel для вычисления параметров линейной зависимости. 12
5. Нелинейная аппроксимация эмпирических данных. 15
6. Выбор наилучшей эмпирической зависимости. 20
7. Задания для самостоятельной работы.. 20
Введение
На практике мы часто сталкиваемся с задачей о сглаживанииэкспериментальных зависимостей. Возможным вариантом решения этой задачи является интерполирование.При этом следует отметить, что при большом количестве экспериментальных точек или узлов этот метод является неудобным и достаточно сложным, ибо требует отыскания многочлена большой степени. Такой способ требует обязательного совпадения табличных значений табличной и приближающей функций во всех заданных табличных аргументах и, таким образом, во многих случаях оказывается совершенно нецелесообразным.
|
|
|
Так, например, этот метод также мало пригоден, если речь идет об обработки каких-либо наблюдаемых или экспериментальных данных, полученных в результате наблюдений или измерений ибо экспериментальные данные всегда содержат ошибки различного рода (систематические, случайные и грубые).
Основы метода наименьших квадратов
Пусть зависимость между двумя переменными х и у выражаетсялибо ввиде таблицы (Таблица. 1), либо в виде набора точек 
где 
Как правило, такие данные могутбыть результатами опыта или наблюдений, статистической обработкиматериала и т.п. и, следовательно, имеют погрешности.
| х | x1 | x1 | … | xn |
| у | y1 | y2 | … | yn |
Таблица 1. Эмпирические или экспериментальные данные
Задача состоит в том, чтобы наилучшим образом сгладить экспериментальнуюзависимость между переменными х и у, получив относительно простую функциональную зависимость, которая по возможноститочно отражает общую тенденцию зависимости у от х, исключивпри этом случайные отклонения, связанные с неизбежными погрешностямиизмерений или статистических наблюдений и позволяющая вычислять значения функции в точках несодержащихся в исходной таблице. Такуюсглаженную зависимость стремятся представить в видеформулы
|
|
|
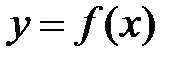(1)
Формулы, служащие для аналитического представленияопытных данных, получили название эмпирических формул.
Задача нахождения эмпирических формул для установленной из эксперимента функциональной зависимости разбивается на дваэтапа. На первом этапе устанавливается вид зависимости.
Поиск эмпирической формулы 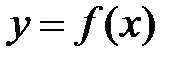начинается с определения класса функций, которыелучше всего отражают связь между табличными данными.Очень часто для выбора функции 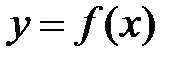привлекаются дополнительныесоображения, как правило, не математическогохарактера (теоретические предпосылки, опыт предшествующихисследований и т.п.).Если же вид эмпирической зависимости неизвестен, то эффективным методом дляего установления являются графические изображения. На координатной плоскости отмечаютсяопределяемые данной функцией точки, а затем по характеру их расположенияподбирается вид приближения из числа известных элементарных функций (Рис. 1).
|
|
|
В перечень наиболее часто используемых классов функций входят, например, линейные 
полиномиальные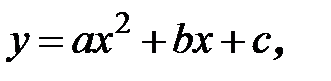 
логарифмические 
экспоненциальные 
степенные 
дробно-рациональные 
гиперболические 
и другие функциональные зависимости.
| 0 |
| у |
| х |
Рис.1. Графическое представление задачи аппроксимации эмпирических данных
Второй этап — определение неизвестных параметров выбранной функции.В общем случае выбранная функция 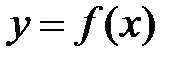будет зависеть от m неизвестных параметров, то есть 
Так, например, самая простая линейная функция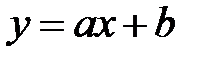 
имеет два параметра а и b.Для каждойзаданной точки определяется величинаневязок 
, которые представляют собой отклонение теоретических значений 
, найденных по эмпирической формуле, от соответствующих опытных значений 
, т.е.
(2)
Нетрудно заметить, что невязки могут принимать как положительные, так и отрицательные и равные нулю значения. Согласно наиболее распространенному и теоретически обоснованномуметоду наименьших квадратов в качестве неизвестных параметров функции 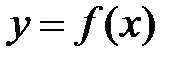выбирают такие значения параметров функции, чтобысумма квадратов невязок была минимальной, т.е.
|
|
|
(3)
Последнее означает, что мы имеем дело с задачей нахождения локального экстремума функции нескольких переменных.
Метод наименьших квадратов в случае линейной эмпирической функции
Пусть в качестве функции 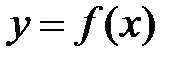взята линейная функция 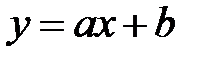. Следовательно, задача сводится к отысканию таких значений двух параметроваи b,при которых функция
(4)
принимает наименьшее значение.
Заметим, что функция 
есть функция двух переменных аи bдо тех пор, пока мы не нашли, а затем зафиксировали их наилучшие (в смысле метода наименьших квадратов) значения, а xiи соответствующие им и найденные экспериментальноyi – постоянные числа.
Задача общей теории нахождения экстремума функции двух переменных сводиться к решению системы уравнений
или 
(5)
После алгебраических преобразований системы (5), она принимаетвид:
(6)
Такая система называется системой нормальных уравнений. Доказано, что система нормальных уравнений имеет единственное решение, при котором функция непросто имеет локальный минимум, а принимает наименьшее значение (глобальный минимум).
Решение системы нормальных уравнений можно представить в виде:
(7)
где 
Замечание.Нетрудно заметить, что смысл последних величин состоит в том, что они представляют собой средние арифметическиесоответственно переменных х и у, квадрата переменной х и произведения х на у.
Дата добавления: 2018-05-12; просмотров: 306; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!