Простые статистические методы
Среди простых статистических методов, названных так ввиду их сравнительной несложности, убедительности и доступности, наибольшее распространение получили семь методов, выделенных в начале 50-х годов японскими специалистами под руководством К. Исикавы. С их помощью, по свидетельству самого К. Исикавы, может решаться от 50 до 95 % всех проблем, находящихся в поле зрения производственников.
Семь простых методов могут применяться в любой последовательности, в любом сочетании, в различных аналитических ситуациях, их можно рассматривать и как целостную систему, и как отдельные инструменты анализа. В каждом конкретном случае предлагается определить состав и структуру рабочего набора методов. Хотя они являются простыми методами, но это отнюдь не значит, что при использовании многих из них нельзя воспользоваться компьютером, чтобы быстрее и без затруднений сделать подсчеты и наглядней представить статистические данные.
Согласно К. Исикаве в семь простых методов входят: контрольный листок, диаграмма Парето, временной ряд, причинно-следственная диаграмма, гистограмма, диаграмма разброса (расслоении) данных и контрольная карта [9, с. 133; 13, с. 112].
Контрольный листок служит средством для сбора и упорядочения первичных данных. Он используется для получения ответа на вопрос: как часто встречается изучаемое событие? Форма листка разрабатывается в соответствии с конкретной ситуацией. В любом случае в нем указываются: объект изучения (например, наименование и чертеж изделия или детали); таблица регистрации данных о контролируемом параметре (например, линейный размер изделия или детали); место контроля (цех, участок); должность и фамилия работника, регистрирующего данные; дата; продолжительность наблюдения и наименование контрольного прибора (если он применяется в ходе наблюдения). В регистрационной таблице в графе «отметки» проставляются точки, крестики и др. условные знаки, соответствующие количеству наблюдений.
|
|
|
Диапазон применения контрольных листков очень широк, а их виды весьма разнообразны. При подготовке контрольных листков нужно следить за тем, чтобы использовались наиболее простые способы их заполнения (цифры, условные значки); чтобы число контролируемых параметров было по возможности наименьшим; чтобы форма листка была проста для заполнения и анализа. Бланки контрольных листков должны быть напечатаны на бумаге, исключающей расплывание чернил, и иметь удобный для хранения и пользования формат.
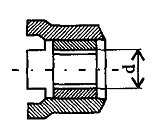
На рис. 16 показан образец контрольного листка, в котором зафиксированы результаты контроля диаметра полумуфт, изготовленных на токарном станке в течение нескольких дней.
|
|
|
| Наименование детали | Полумуфта для соединения валов | ||||
| Наименование операции | Чистовая расточка посадочного отверстия | ||||
|
| Объект контроля | Внутренний диаметр d = 31,3 + 0,2 мм | |||
| Измерительные средства | Предельные калибры | ||||
| Фамилия изготовителя | Иванов К. А. | ||||
| Фамилия контролера | Ветров В. П. | ||||
|
| |||||
| Дата | Количество проверенных деталей (n), шт. | Количество дефектных деталей | Доля дефектных деталей (Р = х/n 100), % | ||
| точечные отметки | (х), шт. | ||||
| 10.10.88 | 100 | : | 2 | 0,02 | |
| 11.10.88 | 100 | 0 | 0 | ||
| 12.10.88 | 100 | 0 | 0 | ||
| 13.10.88 | 100 | :. | 3 | 0,03 | |
| 14.10.88 | 100 | · | 1 | 0,01 | |
| 15.10.88 | 100 | · | 1 | 0,01 | |
| 17.10.88 | 100 | 0 | 0 | ||
| 18.10.88 | 100 | 0 | 0 | ||
| 19.10.88 | 100 | 0 | 0 | ||
| 20.10.88 | 100 | :: | 4 | 0,04 | |
| 21.10.88 | 100 | 0 | 0 | ||
| 22.10.88 | 100 | 0 | 0 | ||
| 24.10.88 | 100 | · | 1 | 0,01 | |
| 25.10.88 | 100 | 0 | 0 | ||
| Итого: | n = 1400 | Σ х = 12 | Р = х/n 100 = 12/1400×100 = 0,85 % | ||
Рис. 16 Образец контрольного листка
Временной ряд (линейный график) применяется, когда требуется самым простым способом представить ход изменения наблюдаемых данных за определенный период времени [14, с. 116].
Временной ряд предназначен для наглядного представления данных, он очень прост в построении и использовании. Точки наносятся на график в том порядке, в каком они были собраны. поскольку они обозначают изменение характеристики во времени, очень существенна последовательность данных.
|
|
|
Опасность в использовании временного ряда заключается в тенденции считать важным любое изменение данных во времени.
Временной ряд, как и другие виды графической техники, следует использовать, чтобы сосредоточить внимание на действительно существенных изменениях в системе.
Одно из наиболее эффективных применений временного ряда заключается в выявлении существенных тенденций или изменений средней величины (рис. 17).

Рис. 17 Временной ряд
Диаграмма Парето – разновидность столбиковой диаграммы, применяемой для наглядного отображения рассматриваемых факторов в порядке уменьшения их значимости. Идея этой диаграммы принадлежит Дж. Джурану, который использовал в качестве ее основы кумулятивную кривую американского экономиста Лоренца, построенную на основе теории распределения доходов, выдвинутой итальянским экономистом Парето [10, с. 162].
Для построения диаграммы Парето исходные данные представляют в виде таблицы, в первой графе которой указывают анализируемые факторы, во второй – абсолютные данные, характеризующие число случаев обнаружения анализируемых факторов в рассматриваемый период, в третьей – суммарное число факторов по видам, в четвертой – их процентное соотношение и в пятой – кумулятивный (накопленный) процент случаев обнаружения факторов. В табл. 7 приведен пример обработки исходных данных для построения диаграммы Парето в случае анализа изготовления литых деталей.
|
|
|
Таблица 7 Данные для построения диаграммы Парето
| Виды несоответствий деталей | Количество несоответствий | Суммарное количество несоответствий | Процентное соотношение несоответствий по видам | Кумулятивный процент несоответствий |
| 1 | 2 | 3 | 4 | 5 |
| Усадочные раковины Газовая пористость Горячие трещины Неметаллические включения Прочие несоответствия | 48 32 23 4 8 | 48 80 103 107 115 | 41,7 27,8 20,0 3,5 7,0 | 41,7 69,5 89,5 93,0 100,0 |
| Итого | 115 | – | 100,0 | – |
Начинают построение диаграммы Парето с того, что на оси абсцисс откладывают данные графы 1, а на оси ординат – данные графы 2, располагаемые в порядке убывания частоты встречаемости. «Прочие факторы» всегда располагают на оси ординат последними; если доля этих факторов сравнительно велика, то необходимо сделать их расшифровку, выделив при этом наиболее значительные. По этим исходным данным вычерчивают столбиковую диаграмму (рис. 16), а затем, используя данные графы 5 и дополнительную ординату, обозначающую кумулятивный процент, вычерчивают кривую Лоренца. Возможно, построение диаграммы Парето, когда на основной ординате откладывают данные графы 4; в этом случае для вычерчивания кривой Лоренца нет необходимости включать в диаграмму дополнительную ординату (именно этот вариант диаграммы наиболее распространен на практике).
Определяющим достоинством диаграммы Парето является то, что она дает возможность разгруппировать факторы на значительные, т. е. встречающиеся наиболее часто, и на незначительные, т. е. встречающиеся относительно редко. Так, анализ диаграммы, представленной на рис. 18 (а также кривой Лоренца), показывает, что усадочные раковины, газовая пористость и горячие трещины в литых деталях составляют 89,5 % всех несоответствий. Следовательно, с устранения именно этих несоответствий следует начинать работу по обеспечению качества деталей.

Рис. 18 Диаграмма Парето по видам дефектов литья деталей:
1 – усадочные раковины; 2 – газовая пористость; 3 – горячие трещины;
4 – неметаллические включения; 5 – прочие дефекты
Построение диаграммы Парето часто обнаруживает закономерность, получившую название «правило 80/20» и основанную на принципе Парето, согласно которому большая часть следствий вызывается относительно немногочисленными причинами. Применительно к анализу несоответствий данная закономерность может быть сформулирована следующим образом: обычно 80 % обнаруженных несоответствий связано лишь с 20 % всех возможных причин. По выражению Д. Кернса, метод Парето позволяет отделить «насущное многое» от «незначительного малого» и тем самым подчеркивает неравномерность влияния факторов на объем изучения».
Кроме выявления и ранжирования факторов по их значимости, диаграмма Парето с успехом применяется для наглядной демонстрации эффективности тех или иных мероприятий в области обеспечения качества. Достаточно построить и сравнить две диаграммы Парето – до и после реализации каких-либо мероприятий.
Причинно-следственная диаграмма предложена в 1953 г. К. Исикавой. Она получила название «схема Исикавы» (в японской литературе эту диаграмму из-за ее формы часто именуют «рыбьей костью» или «рыбьим скелетом»). Схема представляет собой графическое упорядочение факторов, влияющих на объект анализа. Главным достоинством схемы Исикавы является то, что она дает наглядное представление не только о тех факторах, которые влияют на изучаемый объект, но и о причинно-следственных связях этих факторов (что особенно важно) [9, с. 139].
На рис. 19 показан принцип построения схемы Исикавы. При вычерчивании схемы Исикавы к центральной горизонтальной стрелке, изображающей объект анализа, подводят большие первичные стрелки, обозначающие главные факторы (группы факторов), влияющие на объект анализа. Далее к каждой первичной стрелке подводят стрелки второго порядка, к которым в свою очередь подводят стрелки третьего порядка и т. д. до тех пор, пока на диаграмму не будут нанесены все стрелки, обозначающие факторы, оказывающие заметное влияние на объект анализа в конкретной ситуации. Каждая из стрелок, нанесенная на схему, представляет собой, в зависимости от ее положения, либо причину, либо следствие: предыдущая стрелка по отношению к последующей всегда выступает как причина, а последующая как следствие.
Наклон и размер не имеют принципиального значения. Главное при построении схемы заключается в том, чтобы обеспечить правильную соподчиненность и взаимозависимость факторов, а также четко оформить схему, чтобы она хорошо смотрелась и легко читалась. Поэтому, независимо от наклона стрелки каждого фактора, его наименование всегда располагают в горизонтальном положении, параллельно центральной оси.
Несмотря на относительную простоту, построение схемы Исикавы требует от ее исполнителей хорошего знания объекта анализа и понимания взаимозависимости и взаимовлияния факторов. При структурировании схемы на уровне первичных стрелок факторов во многих реальных ситуациях можно воспользоваться предложенным самим Исикавой правилом «пяти М». Оно состоит в том, что в общем случае существуют следующие пять возможных причин тех или иных результатов: материалы, машины, технология (методы), измерения, люди. Все эти слова по-английски начинаются с буквы «М», откуда и пошло название данного правила. Разумеется, могут быть и другие структурирующие факторы, более часто характеризующие конкретный объект анализа. Важно, что сам процесс построения схемы побуждает разработчиков к творческому поиску и обучает их системному мышлению. Развернутая, т. е. достаточно детализированная схема Исикавы может служить основой для составления плана взаимоувязанных мероприятий, обеспечивающих комплексное решение поставленной при анализе задачи.

Рис. 19 Принцип построения диаграммы Исикавы
С помощью схемы Исикавы можно не только определить состав и взаимозависимость факторов, влияющих на объект анализа, но и выявить относительную значимость этих факторов. Работа по определению значимости факторов может быть организована следующим образом. Разработанная схема вычерчивается на учебной доске или на листе ватмана. Все члены группы анализа, независимо друг от друга, отмечают на имеющихся у них копиях этой схемы три наиболее значимых, по их мнению, фактора. Затем каждый член группы подходит к доске и отмечает на рабочей схеме кружками «свои», например, три стрелки-фактора; в случае, если стрелка уже помечена кружком, новый кружок вычерчивается вокруг предыдущего. В конечном итоге после того, как все члены группы отметят свои варианты, на схеме выявится – по наибольшему числу концентрических колец на стрелках – три наиболее значимых, с точки зрения всех членов группы, фактора. На рис. 20 показан результат определения группой из пяти членов относительной значимости факторов, вызывающих несоответствие стандарту качества динамика акустической колонки. Из диаграммы следует, что наиболее значимыми (в соответствии с числом концентрических колец на стрелках-факторах) являются консистенция клея (4 кольца), деформация демпфера (3 кольца) и невнимательность (небрежность) исполнителей-сборщиков (3 кольца).

Рис. 20 Схема Исикавы с оценками значимости факторов,
вызывающих брак динамика акустической колонки
Гистограммапредставляет собой один из видов столбиковой диаграммы, дающей наглядное изображение того, с какой частотой повторяется то или иное значение или группа значений [14, с. 119]. Гистограмма показывает размах изменчивости процесса, помогает понять и проанализировать его динамику. При вычерчивании гистограммы совокупность прямоугольников располагают на горизонтальной оси. Основаниями прямоугольников в этом случае являются интервалы шириной d, на которые разбивается ряд значений, а ординатами – относительные частоты А, характеризующие число значений, попавших в каждый интервал.
Гистограмма широко применяется при контроле качества деталей и готовой продукции, при изучении количественных закономерностей производственных процессов, при оценивании уровня качества продукции и труда по периодам наблюдений.
Построение гистограммы ведется в следующей последовательности. Сначала составляют таблицу исходных данных. Для заполнения таблицы предварительно определяют количество интервалов по формуле:
К = 1 + 3,3 lg n, (4)
где n – объем выборки, т. е. количество исходных данных (рекомендуется К принимать в пределах 6–10 при п = 100–150 и К = 10–20 при n > 150; для получения достоверной картины при построении гистограммы n должен быть не менее 100.
Затем оценивают размах анализируемого параметра по формуле:
R= Xmax – Xmin (5)
и определяют ширину размаха по формуле:
d= R/К. (6)
Устанавливают точку отсчета первого интервала (например, в точке Xmin). Выбирают окончательное количество интервалов. При этом необходимо, чтобы dK = R, a ширина интервала была бы не менее, чем в 2 раза больше цены деления измерительного средства для компенсации погрешности измерения (если ширина интервала равна цене деления измерительного средства, то при построении получается не гистограмма, а полигон частот).
Вид гистограммы зависит от объема выборки, количества интервалов, начала отсчета первого интервала. Чем больше объем выборки и меньше ширина интервала, тем ближе гистограмма к непрерывной кривой.
На рис. 21 показана гистограмма распределения диаметра заготовок шестерен, полученных на токарном автомате. Гистограмма построена по данным таблицы; ширина интервала (d) в рассматриваемом примере принята равной 0,1 мм; объем наблюдений п = 200.


Рис. 21 Таблица распределения частот и
гистограмма распределения диаметра заготовок шестерен
Из данной гистограммы могут быть сделаны следующие выводы:
· большинство (94 %) изготовленных на токарном автомате заготовок укладывается в технологический допуск (30–0,5 мм);
· количество заготовок со значительным несоответствием (диаметр ниже 29,5 мм) составляет 4 %;
· выпуска заготовок несоответствующего качества можно избежать, если настройку автомата осуществить на размер, меньший на 0,1 мм.
Анализ формы распределения гистограммы и ее расположения по отношению к технологическому допуску позволяет делать заключения о состоянии изучаемого процесса и вырабатывать надлежащие меры.
Диаграмма разброса (диаграмма рассеивания) применяется для выяснения зависимости одной переменной величины (показателя качества продукции, параметра технологического процесса, величины затрат на качество и т. п.) от другой [14, с. 120]. Диаграмма не дает ответа на вопрос, служит ли одна переменная величина причиной другой, но она способна прояснить, существует ли в данном случае причинно-следственная связь вообще и какова ее сила.
Наиболее распространенным статистическим методом выявления подобной зависимости является корреляционный анализ, основанный на оценке коэффициента корреляции (от лат. corelato – соотношение). Взаимосвязь изучаемых величин может быть полной, т. е. функциональной, когда коэффициент корреляции равен единице (+1, если переменные одновременно возрастают или убывают, и –1, если при возрастании одной переменной другая убывает). Примером функциональной связи может служить твердость материала заготовки: чем выше твердость, тем больше износ. В том случае, когда взаимосвязь совсем отсутствует, коэффициент корреляции равен нулю. Возможен и промежуточный случай, когда зависимость связанных величин неполная, так как она искажена влиянием посторонних, дополнительных факторов. Иллюстрацией подобного рода корреляционной связи может служить зависимость производительности труда рабочих от их стажа при воздействии таких дополнительных факторов, как образование, здоровье и т. д. Чем больше влияние этих дополнительных факторов, тем менее тесна связь между стажем и производительностью труда. Именно такие связи изучает корреляционный анализ.
Корреляционные связи описываются уравнениями. Например, простейшими корреляционными уравнениями связи между двумя переменными х и у является уравнение прямой вида у = а + bх. Если представить такую связь графически, то она прошла бы через все наблюдаемые точки у. При корреляции соответствие наблюдается лишь приблизительно, и точки наблюдений располагаются не по прямой, а в виде рассеянного «облачка», более или менее вытянутого в некотором направлении. Поэтому приходится, прибегая к специальным приемам, находить ту линию, которая наилучшим образом отражает корреляционную зависимость, т. е. главную направленность «облачка» (рис. 22).

Рис. 22 Корреляционные зависимости: а – сильная положительная
корреляция; б – сильная отрицательная корреляция; в – слабая
положительная корреляция; г – слабая отрицательная корреляция;
д – отсутствие корреляции
В тех случаях, когда требуется выяснить зависимость одного параметра от нескольких других, применяется регрессивный анализ. Для выявления влияния отдельных факторов на исследуемый параметр применяется дисперсионный анализ, при котором исходят из того, что существенность каждого фактора в отдельных условиях характеризуется его вкладом в дисперсию результата эксперимента. Однако техника регрессионного и дисперсионного анализа более сложна, чем техника корреляционного анализа, и построение диаграмм разброса в этих случаях требует от их исполнителей инженерной подготовки.
Контрольная карта – карта, на которой для наглядности отображения состояния анализируемого процесса отмечают значения регулируемой характеристики во времени. Контрольная карта позволяет следить за состоянием процесса во времени, и более того, воздействовать на этот процесс до того, как он выйдет из-под контроля. Первая контрольная карта была предложена в 1924 г. Шухартом [10, с. 167].
Как правило, контрольная карта строится на бланке (формуляре), на который нанесена сетка из тонких вертикальных и горизонтальных линий. По вертикали на карте отмечают выбранную статистическую характеристику наблюдаемого параметра (например, индивидуальное или среднее арифметическое значение, медиану, размах и др.), а по горизонтали – время или номер контрольной выборки. Так, на карту средних арифметических значений предварительно наносят: горизонтальную центральную линию, соответствующую значению центра допуска ЦД (при этом значении технологическая операция считается оптимально налаженной); две горизонтальные линии пределов установленного нормативной документацией технологического допуска (верхнего Тв и нижнего Тн); две горизонтальные линии, являющиеся границами регулирования значений контролируемого параметра (верхняя Pв и нижняя Рн). Границы регулирования ограничивают область значений регулируемой выборочной характеристики, соответствующей удовлетворительной наладке технологической операции (если контролируемый параметр задан односторонней нормой, то на контрольную карту наносится только одна граница регулирования). Для лучшего восприятия контрольной карты ее центральную линию и границы целесообразно обозначать разными цветами, например, центральную линию – зеленым, допусковые границы – красным, границы регулирования – черным.
Границы регулирования рассчитываются с учетом принятого распределения значений контролируемого параметра и дополнительной вероятности получения ложного предупредительного сигнала о разладке операции. Доверительный интервал указывает, внутри каких границ ожидается истинное значение статистической характеристики.
Сущность работы с контрольной картой сводится к тому, что по данным наблюдения за значениями контролируемого параметра устанавливается, находится ли этот параметр в границах регулирования, и на основании этого принимается решение о том, налажена технологическая операция или разлажена.
Решение о разладке операции принимается при выходе хотя бы одного наблюдения, фиксируемого на карте в виде точки, за границы регулирования. Однако еще до выхода точек за границы регулирования контрольная карта дает возможность судить о наметившихся нарушениях технологической операции по следующим признакам:
· вблизи границ регулирования появляются несколько последовательных значений контролируемого параметра,
· значения распределяются по одну сторону от центральной линии, т. е. среднее значение смещается относительно центра настройки
· значения контролируемого параметра сильно разбросаны,
· намечается тенденция приближения значений контролируемого параметра к одной из границ регулирования.
В настоящее время существует множество различных типов контрольных карт. Однако в рамках семи простых методов используются главным образом всего лишь четыре типа:
· индивидуальных значений, xi-карта,
· средних арифметических значений, x-карта,
· средних арифметических значений и размахов, (x–R)-карта,
· медиан и размахов, (m–R)-карта.
Карты средних арифметических значений и медиан применяют для технологических операций, в которых разладка характеризуется смещением установки, а рассеивание в ходе операции практически остается неизменным (например, при механической обработке). Карта средних арифметических значений предпочтительна при сложных настройках технологических операций и жестких допусках, а карта медиан – в случае, когда имеется достаточный запас технологической точности оборудования. При одинаковых условиях карта средних арифметических значений требует меньшего объема выборки, чем карта медиан, примерно в 1,5 раза. Однако определение медианы менее трудоемко, чем вычисление среднего арифметического значения.
Все перечисленные карты относятся к типу карт Шухарта.
На рис. 23 показана контрольная карта средних арифметических значений, построенная на основе контроля размеров цапфы после ее шлифовки. Анализ карты показывает, что технологическая операция шлифования разлажена, так как одна из точек в выборке № 20 вышла за пределы границы регулирования, и, следовательно, необходимо принять меры для устранения причин помех.
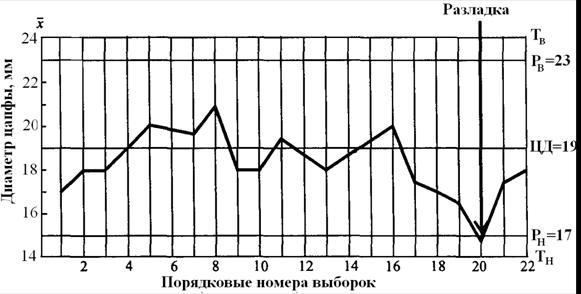
Рис. 23 Контрольная карта средних арифметических
значений (x-карта)
Кроме указанных выше карт, которые используют для статистического регулирования технологических процессов по количественному признаку, в современной практике применяют также q-карты, qn-карты, с-карты u-карты для регулирования по альтернативному признаку и карты на основе метода группировок для регулирования по качественному признаку. Более подробно со статистическим регулированием технологических процессов с помощью этих карт можно ознакомиться по специальным работам.
В дополнение к семи простым методам в 1977 г. специально образованным комитетом Японского союза ученых и инженеров после длительного (в течение 5 лет) и тщательного отбора среди различных методов активизации творческой деятельности и управления были предложены еще семь новых методов. Эти методы призваны решать те 5 % проблем в области качества, которые не могут быть решены с помощью семи простых методов. Особенностью новых методов является то, что они предназначены для обработки, главным образом, словесных (описательных) данных. Реализация новых методов требует углубленной аналитической работы и развитого логического мышления от тех, кто их применяет.
Ввиду своей относительной сложности использование новых методов ограничивается специалистами. В число семи новых методов входят: метод диаграммы сродства; метод графика связей; метод иерархической структуры («метод дерева»); метод матричной диаграммы; метод блок-схемы принятия решений.
Дата добавления: 2018-05-12; просмотров: 1167; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!