Глава 2. Показатели надежности
Для характеристики свойств надежности введены показатели надежности, которые подразделяются на единичные, характери-зующие одно из свойств, составляющих надежность объекта, и комплексные,характеризующие несколько свойств,составляющихнадежность объекта.
К показателям, характеризующим безотказность объекта, относятся:
– вероятность безотказной работы P (t);
– вероятность отказа Q (t);
– интенсивность отказов λ (t);
– средняя наработка до отказа T;
– гамма-процентная наработка до отказа Tγ;
– параметр потока отказов ω (t);
– средняя наработка на отказ T.
Для характеристики долговечности объекта введены показа-
тели:
– средний ресурс T р ;
– гамма-процентный ресурс Tγ ;
– средний срок службы T сл ;
– гамма-процентный срок службы Tγ . Ремонтопригодность характеризуется показателями:
– вероятность восстановления P (tв);
– среднее время восстановления Tв;
– средняя трудоемкость восстановления Qв.
15
К комплексным показателям надежности относятся:
- коэффициент готовности Kг;
- коэффициент оперативной готовности Kог;
- коэффициент технического использования Kти.
Глава 3. Надежность невосстанавливаемого элемента
3.1. Вероятность отказа и вероятность безотказной работы
Будем считать, что время безотказной работы t (наработка) есть какая-то случайная величина ξ с функцией распределения F(t), для которой существует плотность f(t)=F’(t)=dF(t)/dt.
|
|
|
Функция распределения F(t)=P(ξ<t) есть вероятность того, что на интервале времени [0, t] произойдет отказ, или величина случайной наработки ξ будет меньше заданной величины t. Назо-вем функцию распределения вероятностью отказа и обозначим символом Q(t)
F(t)=Q(t)=P(ξ<t). (3.1)
Дополнительную вероятность
| P(t)=1-Q(t)=P(ξ ≥ t) | (3.2) |
будем называть вероятностью безотказной работы. Следователь-но, вероятность безотказной работы есть вероятность того, что элемент будет работоспособным в заданный момент времени, или это есть вероятность того, что случайная величина наработки ξ будет больше заданного времени t.
Известно, что если случайная величина наработки ξ имеет плотность функции распределения f(t)=F’(t) , тогда
P(t)=∞∫ f (x)dx;
t
(3.3)
t
Q( t ) = ∫ f ( x )dx.
0
Плотность функции распределения* f(t) назовем плотностью вероятности отказов
16
| dQ ( t ) | (3.4) | |
| f ( t )=. | ||
| dt |
Плотность вероятности отказов характеризуется вероятно-стью отказов в единицу времени на интервале [0, t].
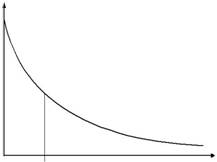
На рис.3.1 показана графическая интерпретация представ-ленных зависимостей.
|
|
|
| f(t) | ||
| Q(t1) | P(t1) | |
| 0 | t | |
| t1 |
Рис.3.1. Плотность вероятности отказов:
Q(t1) - вероятность отказа, численно равна площади под кривой плотности вероятности отказа, ограниченной справа ординатой, проведенной из точки, соответствую-щей моменту времени t1;
P (t1) -вероятность безотказной работы, численно равна площади под кривой плотности вероятности отказов, ог-раниченной слева ординатой, проведенной из точки, соот-ветствующей моменту времени t1
3.2. Интенсивность отказов
Примем, что на интервале времени [0, t] отказа не произош-ло. Необходимо выяснить, какова вероятность отказа в последую-щую единицу времени ∆t (рис.3.2):
A - событие, в котором на интервале [0, t1] не произошло отказа; B - событие, в котором на интервале [t1, t2] произошел отказ;
С - событие, в котором на интервале [0, t1] не произошло отказа, а на интервале [t1, t2] отказ произошел. Тогда
P( C ) = P( A × B ) = P( A )× P BA .

17
А В

| t | |||||||
| 0 | t1 | ||||||
| t2 | |||||||
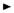
С
Рис.3.2. К расчету вероятности появления события C
|
|
|
В этом случае вероятность события C запишется как
| B | P( C ) | ||||||
| P |
| = | . | (3.5) | |||
| P( A ) | |||||||
| A | |||||||
Вероятность отказа машины в промежутке времени [t1, t2] можно выразить через вероятность безотказной работы
| t2 | ∞ | ∞ | |
| Q(t1t2)=∫ f (t)dt =∫ | f (t)dt −∫ f (t) dt = P( t1 ) − P( t2 ). | (3.6) | |
| t1 | t1 | t2 | |
Тогда вероятность того , что в этом интервале произойдет отказ за единицу времени t2 - t1 , при условии, что отказа не было до момента времени t1, примет вид
| B | (3.7) | ||||||||
| P |
| P (t 1)− | P (t 2 | ) | |||||
| A | = | . | |||||||
| t 2− t 1 | (t 2 − t 1 )× P (t 1 ) | ||||||||
Если записать интервал [t1,t2 ] как [t 1, t1 + ∆t], то
| B |
| |||||
| P |
| P (t )− P (t + ∆ t ) | ||||
| A | ||||||
| = | . | |||||
| ∆ t | ∆ t × P ( t ) | |||||
Это соотношение характеризует ни что иное, как вероят-ность отказов за единицу времени на интервале [t2 – t1] при усло-вии, что до момента времени t1 отказа не было. То есть характери-зует интенсивность отказов на интервале [t1, t2].
|
|
|
Мгновенное значение интенсивности отказов определяется как предел интенсивности отказов на интервале, когда длина ин-тервала стремится к нулю
18
| λ( t )= lim | P (t )− P (t + ∆t ) | = | 1 | − | dP (t ) | = | f (t ) | . | (3.8) | |||
|
|
| |||||||||||
| ∆t ⋅ P (t ) | P( t ) | |||||||||||
| P ( t ) | dt | |||||||||||
И ее можно трактовать как вероятность того, что элемент, доживший до момента t, откажет за последующую (малую) единицу времени. Важность мгновенного значения интенсивности отказов состоит в том, что оно показывает изменение интенсивности отка-зов на протяжении срока службы некоторой совокупности объектов (механизмов, узлов, деталей).
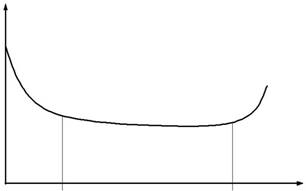
Характерное изменение интенсивности отказов во времени представлено на рис. 3.3.
| λ(t) | ||
| 0 | t | |
| t1 | ||
| t2 | ||
| Рис.3.3. Интенсивность отказов за период службы машины | ||
Для начального периода времени [0, t1] характерны ранние отказы вследствие дефектов материала, конструкторских недора-боток, дефектов изготовления. Этот отрезок кривой получил на-звание период "детской смертности".
Второй отрезок кривой на интервале [t1, t2] отображает слу-чайные внезапные отказы, вызванные неожиданным увеличением нагрузок, предельно тяжелыми условиями работы и т.д.
Отрезок кривой после момента времени t2, характеризует старение объекта, являющееся следствием, как правило, проявле-ния износовых отказов.
Иными словами, интенсивность отказов характеризует изме-нение качества изделия в процессе эксплуатации.
Интенсивность отказов связана с вероятностью безотказной работы соотношением
19
| P ( t )=exp(−∫t | λ (τ ) d τ ), | (3.9) |
| 0 |
а с плотностью вероятности отказов соотношением
| f ( t )= λ ( t ) exp | − | t | (3.10) | |||
| ∫ λ (τ ) d τ | . | |||||
| 0 |
Интенсивность отказов, рассматриваемая на каком-то про-межутке времени, называется накопленной интенсивностью отка-зов Λ(τ) и связана с мгновенным значением интенсивности отказов соотношением
| ∧ (t) = ∫t | λ(τ)dτ, | (3.11) | |
| 0 | |||
| а с вероятностью безотказной работы соотношением | |||
| ∧ (t ) = − ln P (t ) . | (3.12) | ||
| Найдем накопленную интенсивность отказов на интервале | |||
| [t 1, t + x]. | |||
| Из выражения (3.9) следует, что вероятность безотказной ра- | |||
| боты в момент времени t+x | |||
| t+x | |||
| P(ξ 1 ≥ x)= exp - | ∫ | λ(τ )dτ , | (3.13) |
| t | |||
| где ξ1 - остаточное время жизни элемента, | т.е. случайная ве- | ||
| личина, равная (ξ − t) при условии, что ξ > t ; | ξ -время безот- | ||
казной работы элемента.
То есть вероятность отказа элемента, дожившего до момен-та времени t , на очередном интервале [t,t+x] зависит только от
значения функции λ( τ ) на этом интервале и не зависит от ее по-ведения вне этого интервала и может характеризоваться накоп-ленной интенсивностью отказов Л(t,t+x) на интервале [t,t+x].
| Λ(t , t + x)= ln P(t + x) − ln P(t); | (3.14) |
20
Пример 3.1. Долговечность комплекта вкладышей шпинделей со стороны валков в линии привода чистовой группы клетей (7 кле-тей) имеет нормальное распределение с математическим ожидани-ем µ=60 сут и средним квадратичным отклонением σ =10 сут.
1. Построить график плотности распределения отказов и интенсивности отказов на интервале [0, 70 сут].
2. Определить возможное число n1 отказавших комплектов вкладышей к моменту времени t=50 сут.
3. Определить возможное число отказавших комплектов вкладышей n2 на интервале [50 - 60] сут.
4. Определить возможное число отказов вкладышей n3 на
интервале [50-60] сут, если до момента времени t=50 сут отказов не было.
Решение.
Построение графиков осуществим, используя зависимости:
| λ(t)= | f (t) | ; т.е. λ(t )= |
| f (t) | ; |
| |||||||||
| P(t) | |||||||||||||||
| ∞ |
| ||||||||||||||
| ∫ f (t )dt | |||||||||||||||
| t | |||||||||||||||
| t − | µ | ||||||||||||||
| ϕ | t | − | µ | ||||||||||||
| σ | |||||||||||||||
| f (t )= | ; P(t) = 0,5 | − Φ | . | ||||||||||||
| σ |
| σ | |||||||||||||
Возможное число отказавших комплектов вкладышей n1 для t=50, µ=60 учитывая, что Q(t)=1-P(t) и Ф(-z)=-Ф(z):
| n | = N ×Q( t ) = N × | 0 , 5 +Ф | t − | µ | = | |||
|
|
| |||||||
| 1 | σ | |||||||
= 14 × 0 , 5 +Ф 50 − 60 =14 ×( 0 , 5 − 0 , 341) = 2,23,
10

где N – число комплектов вкладышей в чистовой группе клетей со стороны валков; Ф – нормированная функция Лапласа, т.е. функция распреде-
ления (см. табл. 1 прил.Б).
Возможное число отказавших комплектов вкладышей n2 на ин-тервале [50-60] сут, если были отказы в интервале [0-50] сут.
n2= N × P (t1)− P (t2)=14×(0,841−0,5)=4,77,
21
| т.к. | P(t 1 ) | 60 − 50 | ||||||||
| = 0,5 +Ф | 10 | = 0,5 + 0,341 = 0,841 , | ||||||||
| P(t2)=0,5 | ||||||||||
| Возможное число отказов комплектов вкладышей n3 на интер- | ||||||||||
| вале [50-60] сут, если до отказов не было, найдем, используя гра- | ||||||||||
| фик интенсивности отказов на рис.3.4. | ||||||||||
| f (t ) | λ (t ) | λ (t ) | ||||||||
| 150*10 | -3 | |||||||||
| 100*10 | -3 | |||||||||
| 80* | ||||||||||
| 50*10 -3 | ||||||||||
| 40 | ||||||||||
| 24 | 20* | |||||||||
| f (t ) | ||||||||||
| 5.4 | 5.4* | |||||||||
| 30 | 40 | 50 | 60 | 70 | 80 | 90 | t | |||
| Рис.3.4. График плотности распределения отказов | ||||||||||
| и интенсивности отказов для условий примера 3.1 | ||||||||||

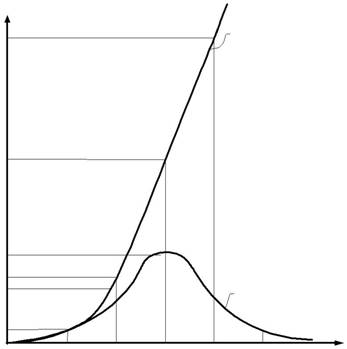
Площадь под кривой интенсивности отказов на интервале [50-60] сут есть вероятность отказов вкладышей на этом интервале при условии, что до этого отказов не было. Тогда возможное число отказов комплектов вкладышей n3 при использовании накопленой интенсивности отказов, определенной по площади ограниченной
кривой ∧ (t ), т.е. приближено в виде трапеции, будет равно
22
|
|
| и дисперсия |
| n = N ×∧( t t | ) =14 ×(60 − 50)× | (80 + 29)×10−3 | = 7,6 | ||
| 3 | 1 2 | 2 | |||
или, более точно, принимая во внимание формулу (3.12):
n3= N ×(ln P(t1)− ln P(t2))=14×( −0,173+0,693 ) =7,3.
3.3. Средняя наработка до отказа и другие числовые характеристики надежности
Очень часто на практике затруднительно оценивать надеж-ность функциональными характеристиками, и в этом случае на-дежность элемента характеризуют числовыми характеристиками. Наиболее важными из них являются: среднее время безотказной
работы (средняя наработка до отказа) T (ξ )
D(ξ )= σ 2 (ξ ),где σ 2 (ξ )-среднее квадратичное отклонение слу-чайной величины ξ :
| ∞ | (t)⋅dt ; | ||||
| T = Tξ | = Mξ | = ∫t ⋅ fξ | (3.15) | ||
| 0 | |||||
| ∞ | ⋅(t )⋅dt ; | ||||
| T = Tξ | = ∫Pξ | (3.16) | |||
| 0 | |||||
| ∞ | |||||
| T = Tξ | = ∫Qξ ⋅(t )⋅dt ; | (3.17) | |||
| 0 | |||||
| D = σ 2 | = Dξ | = ∞∫(t −Tξ )2 ⋅dQξ (t ); | (3.18) | ||
| 0 | |||||
| ∞ | (t )⋅dt −Tξ2 . | ||||
| Dξ =∫t 2 ⋅ fξ | (3.19) | ||||
| 0 | |||||
Следовательно, средняя наработка на отказ есть математи-ческое ожидание Mξ случайной величины наработки ξ , а диспер-сия или среднее квадратичное отклонение служит мерой отклоне-ния случайной величины наработки ξ от ее математического ожи-дания Mξ или, что то же самое, от средней наработки Тξ .
23
На рис.3.4. представлена графическая интерпретация сред-ней наработки и среднего квадратичного отклонения.
Для характеристики степени разброса величин случайной наработки применяют коэффициент вариации , равный отношению среднего квадратичного отклонения к средней наработке:
| ν = | σ . | (3.20) |
| T |

| 1 | ||||||||
| Т | ||||||||
| t) | ) | ) | Ц.Т | |||||
| P( | Т | Q(t | f (t | |||||
| 0 | 0 | |||||||
| t | 0 | t | T | t | ||||
Рис.3.4. Графическая интерпретация средней наработки: Ц.Т. - центр тяжести площади сечения под кривой плотности вероятности отказов
Значения случайной наработки ξ практически не выходят за пределы интервала [T±3σ].
Это правило носит название “правило трех сигм”.
В ряде случаев для характеристики надежности изделия ис-пользуют медианное* значение наработки Meξ. Медиана - это квантиль порядка 0,5. Tо есть Meξ - это значение наработки для вероятности безотказной работы P(t)=0,5.
Значения же наработки для любого заданного значения γ в % вероятности безотказной работы получили название “гамма-процентной наработки Tγ”.
Дата добавления: 2018-05-12; просмотров: 423; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
