Понятие двойственности в линейном программировании. Правила построения двойственных задач

Z=C₁x₁+C₂x₂+...+C_nx_n (2.67)

при условиях

, (2.68)

x_j³0 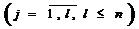(2.69)

О п р е д е л е н и е 1. Задача, состоящая в нахождении минимального значения функции

                            Z^*=b₁y₁+b₂y₂+...+b_ny_n(2.70)

при условиях

                                                                                 (2.71)

                         y_i³ 0                                                                                             (2.72)

называется двойственной по отношению к задаче (2.67)—(2.69).

Задачи (2.67)—(2.69) и (2.70)—(2.72) образуют пару задач, называемую двойственной парой.

правила:

1. Целевая функция исходной задачи задается на максимум, а целевая функция двойственной— на минимум.

2. Матрица

,

составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица

в двойственной задаче получаются друг из друга транспонированием.

3. Число переменных в двойственной задаче равно числу соотношений в системе исходной задачи, а число ограничений в системе двойственной задачи— числу переменных в исходной задаче.

4. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе исходной задачи, а правыми частями в соотношениях системы двойственной задачи — коэффициенты при неизвестных в целевой функции исходной задачи.

5. Если переменная х_j исходной задачи может принимать только лишь положительные значения, то j-е условие в системе (2.71) двойственной задачи является неравенством вида «³». Если же переменная х_j может принимать как положительные, так и отрицательные значения, то j -е соотношение в системе (2.71) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (2.68) исходной задачи и переменными двойственной задачи. Если i-е соотношение в системе (2.68) исходной задачи является неравенством, то i-я переменная двойственной задачи y_i ³0. В противоположном случае переменная y_i может принимать как положительные, так и отрицательные значения.

Леммы и теоремы двойственности (без док)

Л е м м а 1. Если Х — некоторый план исходной задачи (2.73)—(2.75), а Y— произвольный план двойственной задачи (2.76),(2.77), то значение целевой функции исходной задачи при плане Х всегда не превосходит значения целевой функции двойственной задачиприплане Y, т.е. Z(X)£Z^*(Y).

Л е м м а 2. Если Z(X^*)=Z^*(Y^*)для некоторых планов X^*и Y^* задач (2.73)—(2.75) и (2.76),(2.77), то Х^* — оптимальный план исходной задачи, а Y^* — оптимальный план двойственной задачи.

Т е о р е м а 1.(первая теорема двойственности). Если одна из пары двойственных задач (2.73)—(2.75) или (2.76),(2.77) имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой т.е. Z_max=Z*_min..

Если же целевая функция одной из пары двойственных задач не ограничена [для исходной сверху, для двойственной снизу], то другая задача вообще не имеет планов.

Т е о р е м а 2.(вторая теорема двойственности). План Х^*=(х^*₁, х^*₂, ..., х^*_n) задачи (2.73)—(2.75) и план Y^*=(y^*₁,y^*₂,...,y^*_m) задачи (2.76),(2.77) являются оптимальными планами этих задач тогда и только тогда, когда для любого j 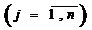выполняется равенство

Дата добавления: 2018-05-12; просмотров: 574; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!