Связь проблемы выбора с задачами ЛП, НЛП, ИГР. 27
1.Проблемные ситуации и их классификация
| Формулировка проблемы | Метод решения | Решение проблемы | ||
| 1 | явные | + | + | + |
| 2 | + | + | - | |
| 3 | + | - | + | |
| 4 | + | - | - | |
| 5 | неявные | - | + | + |
| 6 | - | + | - | |
| 7 | - | - | + | |
| 8 | - | - | - |
Способы решений проблемных ситуаций
Решение – это выбор альтернатив.
Решения бывают:
1.Рациональные
2.Организационные
3.Интуитивные
4.Запрограмированные
6. Решения основанные на суждениях
7.Компромисные
Этапы принятия рационального решения
Принятие решений – особый вид целенаправленной деятельности, заключающийся в выборе одной из имеющихся альтернатив.
1. Диагноз и формулировка проблемы.
2. Определение цели и представления о результате
Общая задача линейного программ (целевая функция, ограничения, план задачи, допустимое множество, оптимальное решение)
Общей задачей линейного программирования (ОЗЛП) называют задачу
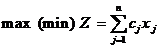 (2.10)
(2.10)
при ограничениях:
 , (2.11)
, (2.11)
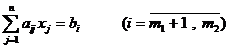 , (2.12)
, (2.12)
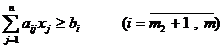 , (2.13)
, (2.13)
 , (2.14)
, (2.14)
|
|
|
xj — произвольные  , (2.15)
, (2.15)
где cj , Aij , bi — заданные действительные числа; (2.10) — целевая функция; (2.11)—(2.15) — ограничения; x = ( x1 , ..., xn ) — план задачи.
Задача о смесях (о диете, о рационе)
Пусть нам известно содержание необходимых для кормления животного питательных веществ в различных применяемых кормах. Известна также цена единицы каждого вида корма. Требуется выбрать рацион — набор и количество кормов — так, чтобы каждое питательное вещество содержалось в нем в необходимом количестве и, кроме того, чтобы суммарные расходы на этот рацион были минимальны.
Введем условные обозначения:
m — число различных необходимых питательных веществ, n — число видов кормов, aij — количество единиц i-го питательного вещества, содержащееся в единице j-го вида кормов, bi — минимальная суточная потребность в i-м питательном веществе, cj — стоимость единицы j-го вида корма, xj — количество единиц j-го вида корма, используемое в рационе и подлежащее определению.
Математическая модель задачи: найти
min 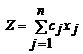
при ограничениях:
 ,
,
 .
.
Задача о наилучшем использовании ресурсов
|
|
|
Пусть некоторая производственная единица (цех, завод, объединение и т. д.) может выпускать n различных видов продукции (товаров), известных под номерами, обозначаемыми индексом j ( j = 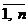 ). Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Обозначим через aij технологические коэффициенты, которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-го вида, через bi — полные объемы имеющихся ресурсов ( j =
). Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Обозначим через aij технологические коэффициенты, которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-го вида, через bi — полные объемы имеющихся ресурсов ( j = 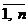 ), cj — прибыль, получаемую при реализации единицы j-го вида продукта.
), cj — прибыль, получаемую при реализации единицы j-го вида продукта.
Требуется составить такой план выпуска продукции, который был бы технологически осуществим по имеющимся ресурсам всех видов, удовлетворял бы задаваемым ограничениям на выпуски каждого вида продукции и в то же время приносил бы наибольшую общую прибыль предприятию.
Таким образом, модель задачи о наилучшем использовании ресурсов состоит в следующем: найти такой план выпуска продукции х=( x1, …; xj, …, xn ), при котором достигался бы

и выполнялись неравенства:
 ,
,
|
|
|
 .
.
Дата добавления: 2018-05-12; просмотров: 407; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
