Теорема о необходимом и достаточном условии существования решения антагонистической игры

Игра называется игрой с нулевой суммой, если сумма выиграшей всех игроков равна нулю (т.е. каждый игрок выигрывает только за счет других). Самый простой случай — парная игра с нулевой суммой — называется антагонистической.

Игра, представленная таким образом, называется матричной, а полученная таблица — платежной матрицей.

основная теорема теории игр: каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.

Правила упрощения матричной игры

Определение оптимальных стратегий и цены игры и составляет процесс нахождения решения игры. Задача решения игры, если ее матрица не содержит седловой точки, тем сложнее, чем больше значения m и n. Сократить размерность матрицы можно, исключая дублирующие и заведомо невыгодные доминирующие стратегии.

           Дублирующими называются стратегии, которым соответствуют одинаковые значения элементов в платежной матрице, т. е. матрица содержит одинаковые строки (столбцы). Если все элементы i-й строки матрицы меньше соответствующих элементов k-й строки, то i-я стратегия для игрока А называется доминирующей. Если же элементы r-го столбца матрицы не меньше соответствующих элементов j-го столбца, то для игрока B стратегия B_r — доминирующая.

            Таким образом, при решении игры m×n следует:

           a) проверить, не содержит ли матрица седловой точки;

           б) если седловой точки нет, то нужно сравнить между собой элементы строк и столбцов для исключения дублирующих и доминирующих стратегий.

 

 

Решение матричной игры 2x2

Матрица А игры имеет вид

А= .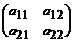

           Если седловой точки нет, то решением игры являются смешанные стратегии U=(u₁, u₂), Z=(z₁,z₂).

           Согласно основной теореме теории игр, применение оптимальной стратегии U=(u₁, u₂) обеспечивает для игрока А получение выигрыша v при любых стратегиях игрока В. Оптимальная стратегия для игрока В также смешанная. Поэтому, если игрок А применяет свою оптимальную стратегию, то при этом игрок В может использовать одну из чистых стратегий, величина выигрыша игрока А останется неизменной. Запишем систему уравнений

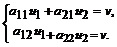
           Так как u₁+u₂=1, то решение таково:

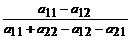u₁= , u₂= .                                                                  (4.3)

Подставляя значения u₁ и u₂ в одно из уравнений (2.1), получаем

v= 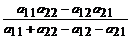.                                                                                        (4.4)

Составляя аналогичную систему уравнений, можно найти оптимальную стратегию для игрока В:

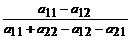z₁= , z₂=                                                                 (4.5)

Геометрическое решение матричной игры Mx2, 2xN

Используя геометрическую интерпретацию, можно найти решение игр, заданных матрицей 2´n. Каждой из n стратегий игрока В соответствует прямая. Построив эти прямые, находят нижнюю границу выигрыша. Точка К, лежащая на нижней границе, для которой величина выигрыша наибольшая, определяет цену игры и ее решение. При этом определяется активные стратегии игрока В (соответствующие им прямые пересекаются в точке К): из геометрических соображений можно найти значения z_j, соответствующие активным стратегиям игрока В.

Аналогично может быть решена игра с матрицей m´2, только в этом случае строят верхнюю границу выигрыша и на ней определяют минимум.

---

Дата добавления: 2018-05-12; просмотров: 752; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!