Критический (псевдокритический) объём

V_Сm =  1/8 S[N_iN_j (V_Сi^1/3 + V_Сj^1/3)]³                                                                    (1.2.2.)

Где V_Сi, V_Сj - критические объёмы компонентов i и j,

Фактор ацентричности для смеси

w_m = S N_iw_i                                                                                                          (1.2.3.)

Коэффициент сжимаемости

 Z_Cm = 0,291 – 0,08 w_m                                                                                        (1.2.4.)

Критическое (псевдокритическое) давление 

Р_Сm = R (Z_CmТ_Сm/ V_Сm)                                                                                       (1.2.5.)

Где М – относительная молярная масса

Коэффициенты парного взаимодействия

Коэффициенты парного взаимодействия k_ij  можно найти в литературе или вычислить по эмпирическим соотношениям [1].

1. Для смесей углеводородов

k_ij  = 0,98 + 0,045 (V_Сi/V_Сj) + 0,0025 (V_Сi/V_Сj)²                                                    (1.2.6)

2. Для смесей, содержащих C₂H₂, H₂S и СО₂.

k_ij  = 0,93 + 0,005 (V_Сi/V_Сj) + 0,0035 (V_Сi/V_Сj)²                                                    (1.2.7)

 

СТРУКТУРНЫЕ КОНСТАНТЫ ВЕЩЕСТВА

Знание критических свойств позволяет вычислить ряд других важных характеристик реальных неидеальных веществ.

1. Фактор ацентричности Питцера (характеризует несферичность структуры молекулы)[11].

w =                                                                                                          (2.1)

        где Q_b. = Т_Vb/ Т_С – приведённая температура кипения;

          [P_КР] = атм.

Фактор сложности

        y = 0,1 lnТ_Vb – 0,122 V_b + 0,006                                                                                            (2.2)

где V_b –объём жидкости при температуре кипения, см³/ моль.

Коэффициенты уравнения Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса – одно из наиболее широко используемых в инженерной практике уравнений

состояния реальных газов.

      (Р+ )(V-b) = RT                                                                                                                 (2.3)

      a= =                                                                                                       (2.3.1)

       b=  =                                                                                                                      (2.3.2)  

Критические параметры связаны соотношением P_CV_C = 3/8 RT_C                                                           (2.3.3)  

Значения констант уравнения Ван-дер-Ваальса для многих газов приведены в литературе [ ]. Уравнение Ван-дер-Ваальса можно представить в безразмерной форме  

(π + 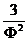)(3Ф -1) =8 Θ                                                                                                                       (2.3.4)  

где π = Р/Р_С - приведённое давление;

Ф = V/V_С - приведённый объём;

Θ= Т/Т_С - приведённая температура.

 

Парахор

Парахор – одна из важных структурных (конститутивных) характеристик вещества, - определяется выражением

 П = , Дж^1/4 см^5/2 моль^-1.                                                                                    (2.4)

Где M_M – относительная молярная масса;

  s - поверхностное натяжение, Дж/м²;

r_Ж, r_П – плотность жидкости и пара, кг/м³.

Данные о значениях парахора приведены в ряде справочников [ ] Наиболее точно значение парахора можно вычислить по следующим формулам

             ₃ __________

П= 0,0183 Ö T_vb V_K^2,2/K                                                                                                              (2.5)

   Где   

         K = 1                         при y < 0,08                                                                              (2.5.1)

 K = 4,675y +0,656 при y > 0,08                                                                              (2.5.2)

Или

П= T_C exp (-7,4y - 4,76)                                                                                                            (2.6)

Погрешность расчётов по формулам (2.5) и (2.6) не превышает 2 %.

ПЛОТНОСТЬ

3.1. ГАЗЫ

3.1.1. ИНДИВИДУАЛЬНЫЙ (ОДНОКОМПОНЕНТНЫЙ) ГАЗ.

Уравнение Менделеева-Клапейрона

Применимо при невысоких - до 1 МПа - давлениях.

r = M_mP/RT                                                                                                                               (3.1.1)

 M_m – молярная масса газа, кг/кмоль.

Если известна плотность газа при одном значении температуры и давления, то для иных условий плотность определяется выражением

r = r₀                                                                                                                                  (3.1.2)

Где r₀ – плотность при опорных (известных) значениях температуры и давления, кг/м³;

  Р, Р₀ – расчётное и опорное абсолютное давление, Па;

Т, Т₀ – расчётная и опорная абсолютная температура, К.

Значения r₀ для многих важных газов приведены в литературе [ ].

Уравнение Ван-дер-Ваальса

Применимо при давлениях до (2…4) МПа. Существенно точнее уравнения Менделеева-Клапейрона, однако получаемые выражения намного сложнее.

         r =                                                                                                             (3.1.3)

V = V_C    -  - молярный объём                                 (3.1.4)

Где Q =                                         |                                                                 (3.1.4а)

  q = 2 }  безразмерные параметры                       (3.1.4б)

  p =                            |                                                                    (3.1.4в)

Ввиду сложности  расчётных выражений уравнение Ван-дер-Ваальса следует использовать только при расчёте процессов, протекающих при высоких давлениях. 

 

3.1.2. МНОГОКОМПОНЕНТНЫЙ ГАЗ.

Плотность многокомпонентного газа (смеси газов) можно вычислить, используя любое из приведённых ниже эквивалентных выражений:

---

Дата добавления: 2018-05-12; просмотров: 814; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!