Релятивистские законы для массы и импульса. Основной закон релятивистской динамики. Взаимосвязь энергии и импульса в СТО.

Преобразование энергии и силы в СТО. Релятивистские законы для кинетической энергии и полной энергии.

Второй закон Ньютона в СТО:

Умножая скалярно левую и правую части этого уравнения на dr=vdt, будем иметь: .

Выражение Fdr определяет элементарную работу δA, совершаемую силой над частицей за время dt. Следовательно, правая часть уравнения может рассматриваться как приращение кинетической энергии релятивистской частицы за это же время: .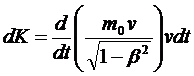

Учитывая, что vdv = d(v²/2) и произведя некоторые тождественные преобразования, можно представить наше уравнение в виде: .

Интеграрование этого выражения приводит к следующему выражению: . Постоянная интегрирования оказывается равной m₀c², поскольку при v = 0 кинетическая энергия частицы должна быть равна нулю. Таким образом, – релятивистское выражение для кинетической энергии.

Первый член в выражении – полная энергия свободной частицы. Второй – энергия покоя E₀ = m₀c².

Таким образом, в релятивистской механике кинетическую энергию частицы можно представить как разность полной энергии и энергии покоя: .

Отсюда следует, что значение кинетической энергии определяет изменение релятивистской массы, вызванное движением этой точки: .

Предмет и задачи молекулярной физики. Термодинамические параметры системы. Законы идеального газа.

Основные положения МКТ газов. Средняя и среднеквадратичная скорости. Опыт Штерна. Средняя длина свободного пробега молекул газа. Эффективный диаметр молекул газа.

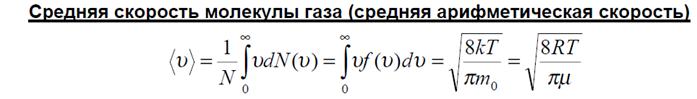
Вывод основного уравнения МКТ газов. Молекулярно-кинетический смысл температуры. Закон Больцмана о равномерном распределении энергии по степеням свободы.

Функция Максвелла для распределения молекул по модулю скорости теплового движения. Тепловые скорости молекул среды.

Функция Больцмана для частиц во внешнем потенциальном поле и ее применение. Барометрическая формула. Функция распределения Максвелла-Больцмана.

Распределение Максвелла-Больцмана.

Для классического идеального газа, движение молекул которого подчиняется механике Ньютона, можно вместо дискретного распределения ввести распределение частиц по скоростям и координатам. В этом случае следует учесть, что энергия ε_i состоит из кинетической энергии и потенциальной энергии во внешнем силовом поле:

Тогда для f = f(v_x, v_y, v_z, x, y, z)запишем функцию распределения Максвелла-Больцмана:

31. Основные понятия термодинамики. Работа. Теплота. Теплоемкость, виды теплоемкостей (удельные (с_p, с_v) и молярные (С_P, С_V)).

Термодинамика изучает процессы, связанные с превращением энергии из одного вида в другой, и характеризует эти превращения с количественной стороны с помощью понятий теплота и работа.

Стационарным называется состояние, для которого значения всех термодинамических параметров постоянны во времени. Стационарное состояние называется равновесным, если его неизменность во времени не обусловлена протеканием каких-либо процессов во внешних по отношению к данной термодинамической системе телах. Равновесное состояние однозначно определяется заданием значений ограниченного числа его термодинамических параметров, называемых параметрами состояния. В случае однокомпанентных систем такими параметрами являются p, V, T, которые связаны между собой уравнением состояния f(p, V, T) = 0.

Внутренней энергией U системы называется сумма кинетической энергии хаотического движения частиц и потенциальной энергии их взаимодействия друг с другом.

При определении внутренней энергии не учитывается кинетическая энергия движения тела как целого и его потенциальная энергия во внешнем силовом поле. Внутренняя энергия системы тел равна сумме внутренних энергий каждого из тел в отдельности и энергии межмолекулярного взаимодействия в тонком слое на границе между телами. Последней из-за ее малости во многих случаях можно пренебречь и считать, что внутренняя энергия системы тел равна сумме внутренних энергий образующих эту систему тел – свойство аддитивности энергии.

Внутренняя энергия является функцией состояния системы.

Внутреннюю энергию системы, зависящую от ее объема V и температуры T (U = U(V, T)), можно изменить двумя различными способами: путем совершения нед термодинамической системой работы A' при постоянной температуре, что связано с изменением ее объема, и путем сообщения ей количества теплоты Q при фиксированном объеме, что приводит к изменению температуры этой системы.

Передача внешними телами энергии в форме работы A' сопровождается макроскопическим перемещением внешних тел. В результате изменяются средние взаимные расстояния между частицами системы, а значит, и их потенциальная энергия. В соответствии с третьим законом Ньютона, система при этом совершает над внешними телами работу A = A'.

Сообщение системе теплоты Q не связано с макроскопическими перемещениями тел системы. Изменение внутренней энергии при теплопередаче состоит в том, что отдельные молекулы более нагретого тела в процессе неупругого столкновения передают часть своей кинетической энергии молекулам менее нагретого тела.

Количество энергии, передаваемой системе внешними телами в форме теплоты, называется количеством теплоты или теплотой Q, сообщаемой системе. Количество теплоты считается положительным, когда оно подводится к системе.

В отличие от энергии системы, являющейся однозначной функцией состояния системы, понятия теплоты и работы имеют смысл только в связи с процессом изменения состояния системы. Теплота и работа – энергетические характеристики термодинамического процесса, обуславливающего переход системы из одного состояния в другое.

Дата добавления: 2018-05-12; просмотров: 1350; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!