Консервативные и неконсервативные силы. Потенциальная энергия консервативных сил.

Работа консервативных сил равна нулю:

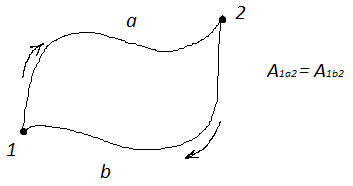

Центральные силы – силы, направленные по радиус-вектору, соединяющие точку с некоторой точкой в пространстве и зависящие только от расстония до этой точки.
Силы, не являющиеся консервативными, называются неконсервативными. Они диссипативные, т. е. связаны с уменьшением работы: A<0. Происходит уменьшение энергии.
Для консервативных сил вводится понятие потенциальной энергии.
Потенциальной называется часть общей механической энергии системы, зависящая от взаимного расположения материальных точек (тел системы) и их положения (координат) во внешнем силовом поле.

Взаимосвязь между потенциальной энергией и силой. Закон сохранения механической энергии замкнутой системы.
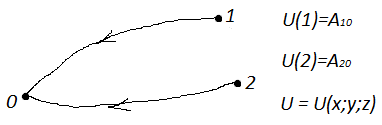
Выберем произвольное положение системы, характеризуемое заданием координат её точек, и примем его за нулевое. Тогда работа, совершаемая консервативными силами при переходе системы из некоторого положения в нулевое, называется потенциальной энергией U.

Разность потенциальных энергий в нулевом положении называется работой, совершаемой консервативными силами при переходе от рассматриваемого положения в нулевое.
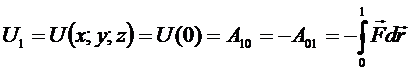
Рассмотрим две бесконечно близкие точки:


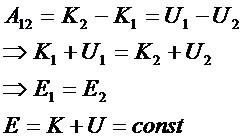
Физическая сущность закона сохранения и превращения энергии – неуничтожимость материи и её движения.
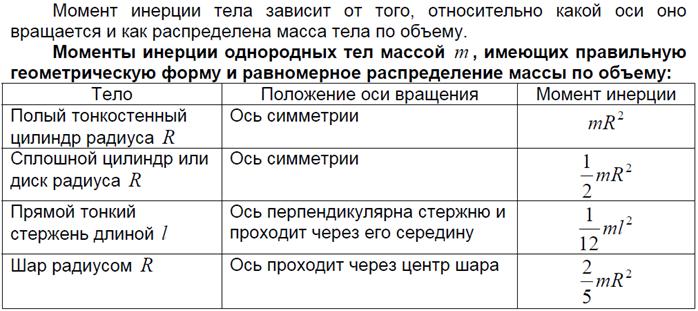
Осевой момент инерции материальной точки и твердого тела. Основное уравнение динамики вращательного движения тела.
|
|
|



Оси инерции тела. Главные моменты инерции тела. Теорема Штейнера.
При рассмотрении вращения вокруг неподвижной оси предполагается, что неизменность направления оси в пространстве обеспечивается внешними условиями (например, подшипниками). При вращении несимметричных тел относительно осей произвольного направления из-за центробежных сил инерции возникают силы бокового давления на подшипники. В случае вращения однородного симметричного тела относительно оси симметрии боковые силы давления не возникают. Тогда при отсутствии внешних сил ось могла бы сохранять неизменным свое положение в пространстве и без крепления в подшипниках. Такие оси называются свободными осями тела.
Для тел произвольной формы и с произвольным распределением массы всегда существуют три взаимно перпендикулярные свободные оси, проходящие через центр масс тела. Такие оси называются главными центральными осями инерции тела.
Момент инерции – физическая величина, количественно характеризующая инертность твёрдого тела, проявляющуюся во вращательном движении.
Момент инерции материальной точки: 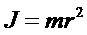 .
.
Момент инерции твердого тела относительно оси вращения:
|
|
|
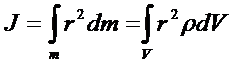
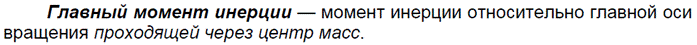

| Прямой тонкий стержень длиной l | Ось проходит через конец стержня | 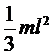
|
| Сплошной диск радиуса R | Ось совпадает с диаметром диска | 
|
| Обруч (обод) | Ось перпендикулярна плоскости обруча и проходит через центр | 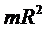
|
| Обруч (обод) | Ось совпадает с диаметром обруча | 
|

Дата добавления: 2018-05-12; просмотров: 466; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
