Раздел 4. Динамическое программирование.

Общая характеристика метода динамического программирования.

В данном разделе рассматриваются детерминированные модели, в рамках которых используется особый подход к принятию оптимального решения. Суть его заключается в разбиении процесса принятия решений на отдельные шаги. Выделение шагов в одних ситуациях базируется на хронологической последовательности, а в других - на логической. Познакомимся с некоторыми основными понятиями метода.

Имеется некоторая управляемая физическая система, в которой происходят процессы, поддающиеся разделению на условные этапы (шаги). На каждом шаге состояние системы характеризуется определенными параметрами. Задача динамического программирования состоит в выборе из множества допустимых решений (управлений) такого, которое переводит систему из начального состояния в конечное, обеспечивая целевой функции экстремум.

В решении задач динамического программирования будем использовать следующие обозначения: - множество состояний, в которых система может находиться перед -м шагом; 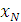- множество конечных состояний; - множество состояний в конце -го шага; - множество управлений, которые могут быть выбраны на -м шаге и под воздействием каждого из которых система переходит в одно из состояний множества 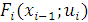_; - условно-оптимальное значение целевой функции на интервалах от -го до N-го включительно при условии, что перед -м шагом система находилась в одном из состояний множества и было выбрано одно из управлений множества ; 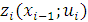- значение целевой функции на -м шаге.

Процедурой метода предусмотрено два способа перемещения в пространстве состояний системы: 1) условная оптимизация – перемещение в обратном направлении ( от последнего шага к первому); 2) безусловная оптимизация – перемещение в прямом направлении ( от первого шага к последнему). Сначала реализуется условная оптимизация, которая позволяет получить экстремальное значение целевой функции. Затем – безусловная оптимизация, в ходе которой мы получаем вектор оптимальных управлений.

В основе условной оптимизации лежит принцип оптимальности Р. Беллмана, который звучит так: каково бы ни было состояние системы в результате осуществления 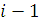шагов, управление на -м шаге должно выбираться так, чтобы оно в совокупности с управлениями на всех последующих шагах, с 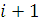-го до N-го включительно, доставляло экстремум целевой функции.

Рассмотрим применение метода на примерах типичных задач.

Задача транспортировки груза по сети дорог.

Пусть физической управляемой системой является транспортное средство с грузом. Груз необходимо доставить из начального пункта движения в конечный, для чего можно выбрать разные маршруты в имеющейся сети дорог. На каждом участке сети определен транспортный тариф на перемещение единицы груза. Требуется доставить груз в конечный пункт, выбрав маршрут с минимальной стоимостью транспортировки.

На рисунке 10 изображена сеть дорог, по которой должен перемещаться транспорт с грузом. Над ребрами сети указаны тарифы.

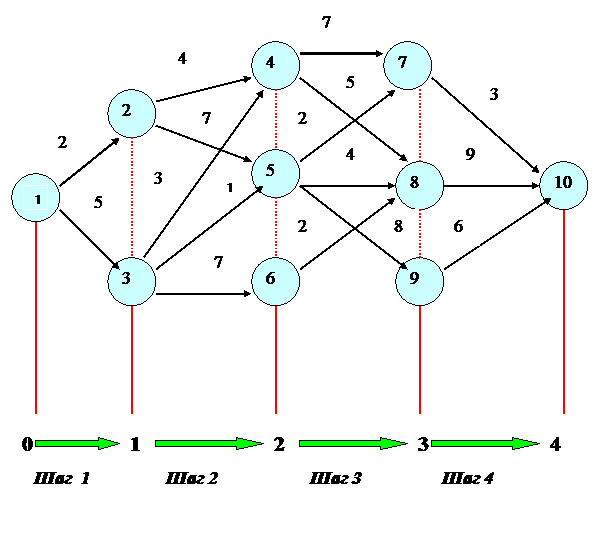
Рис. 10. Схема дорожной сети.

В рассматриваемой задаче используется хронологический принцип выделения шагов, что объясняется физическим смыслом ситуации. Для выделения щагов воспользуемся следующим подходом. Разобьем все пункты сети на группы. К группе 0 отнесем п.1; к группе 1 – пункты, в которые можно попасть непосредственно из п.1; к группе 2 – пункты, в которые можно попасть непосредственно из любого пункта группы 1 и т. д. (см. таблицу 10).

Табл. 10. Группировка пунктов дорожной сети.

Группа 0	Группа 1	Группа 2	Группа 3	Группа 4
п.1	п.2 п.3	п.4 п.5 п.6	п.7 п.8 п.9	п.10

Шагом процесса будем считать перевод транспорта из пунктов предшествующей группы в пункты последующей группы. В результате в данной задаче можно выделить 4 шага, которые показаны на рисунке 10.

Множество состояний системы перед -м шагом представляет собой местонахождение транспорта с грузом в пунктах предшествующей группы. Совокупность управлений на 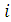-м шаге состоит в выборе дорог, по которым можно направлять груз из данной группы пунктов в последующую. Множество состояний - нахождение груза в пунктах группы, достигнутой в результате реализации -го шага. Элементы множества 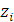– затраты на перевозку единицы груза из данного пункта в выбранный соседний. Множество 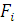- минимальная стоимость транспортировки ( условно-оптимальное значение целевой функции) на шагах от -го до N-го.

Поиск решения начинается с условной оптимизации, в ходе которой процесс анализируется в обратном порядке – от 4-го шага к 1-му. Решение удобно оформлять с помощью таблиц. Каждая таблица отражает элементы обозначенных ранее множеств и завершается выбором условно-оптимальных значений целевой функции.

Таблица 11 содержит анализ 4-го шага.

Табл. 11. Анализ 4-го шага.


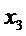
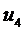
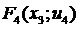
п.7 п.8 п.9	(7,10) (8,10) (9,10)	п.10 п.10 п.10	3 9 6

Перейдем к анализу третьего шага. Из рисунка видно, что множество 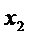включает нахождение груза либо в п.4, либо в п.5, либо в п.6. Множество 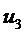включает выбор дорог, ведущих из п.п.4, 5, 6 в п.п. 7, 8, 9. Для п.4 это дороги (4,7) или (4,8); для п.5 – (5,7) или (5,8) или (5,9); для п.6 – (6,8). Множество значений 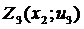состоит из тарифов на перевозку единицы груза по соответствующей дороге.

Условно-оптимальное управление на третьем шаге для каждого из возможных состояний найдем следующим образом. Рассмотрим любое из состояний множества 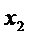. Для перевода системы в состояние множества 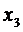существуют следующие возможности:

- из п.4 - (4,7) или (4,8);

- из п.5 - (5;7) или (5,8) или (5,9);

- из п.6 - (6,8).

Используя результаты условной оптимизации 4-го шага, получаем:

F₃(x₂, u₃) = min (7+3; 5+9) = 10,

^{(4,7) (4,8)}

F₃(x_2,u₃) = min (2+3; 4+9; 8+6) = 5,

^{(5,7) (5,8)(5,9)}

F₃(x_2,u₃) = min (2+9) =11.

^(6,8)

Оформим данные рассуждения в виде таблицы анализа 3-го шага (табл. 12).

Таблица 12. Анализ 3-го шага.


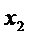
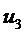
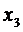
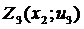
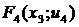
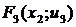
п.4	(4,7) (4,8)	п.7 п.8	7 5	3 9	10 14	10 -
п.5	(5,7) (5,8) (5,9)	п.7 п.8 п.9	2 4 8	3 9 6	5 13 14	5 - -
п.6	(6,8)	п.8	2	9	11	11

Отразим результат анализа 2-го шага в виде таблицы (табл. 13), опустив комментарии. Заметим, что иногда для достижения компактности записи в таблицах используется сокращенное символическое обозначение некоторых показателей.

Таблица 13. Анализ 2-го шага.


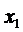
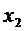
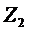
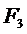
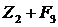
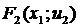
п.2	(2,4) (2,5)	п.4 п.5	4 7	10 5	14 12	- 12
п.3	(3,4) (3,5) (3,6)	п.4 п.5 п.6	3 1 7	10 5 11	13 6 18	- 6 -

Заключительный этап условной оптимизации - анализ 1-го шага отражен в таблице 14. Итог условной оптимизации – экстремальное значение целевой функции. В данном случае это минимальная стоимость транспортировки груза, которая составляет 11 денежных единиц.

Таблица 14. Анализ 1-го шага.


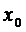
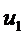
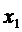
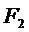
п.1	(1,2) (1,3)	п.2 п.3	2 5	12 6	14 11	- 11

Итак, минимальная стоимость транспортировки определена. Теперь с помощью безусловной оптимизации пройдем процесс в прямом направлении – от 1-го шага к 4-му, путем рассмотрения тех же самых таблиц в обозначенном порядке. Это позволит нам определить вектор оптимальных управлений, или оптимальный маршрут. В выборе компонентов вектора оптимальных управлений следует ориентироваться на условно- оптимальное значение целевой функции и решение, принятое на предшествующем шаге. Так, в таблице 14 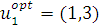определяется по минимальному значению 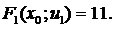В таблице 13 выбирается на основе управления на 1-ом шаге и условно-оптимального значения целевой функции. В последующих таблицах – аналогично. Таким образом, .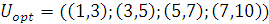

Дата добавления: 2018-05-02; просмотров: 509; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!