Замена переменных в кратных интегралах
Пусть  – области в пространстве
– области в пространстве  ,
,  – гладкое отображение. Через
– гладкое отображение. Через  и
и  будем обозначать точки в
будем обозначать точки в  и
и  соответственно. Возможна другая (покоординатная) запись.
соответственно. Возможна другая (покоординатная) запись.
 ,
,
 ,
,
…
 ,
,
 , где
, где  – дифференцируемы.
– дифференцируемы.
Рассмотрим Якобиан 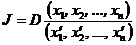 отображения
отображения  , определяемый по формуле
, определяемый по формуле
 .
.
Его можно представить как коэффициент искажения объема.
Теорема (о замене переменных).Пусть  ,
,  – измеримые множества.
– измеримые множества.  – взаимно однозначно на внутренних точках множества
– взаимно однозначно на внутренних точках множества  . Функции
. Функции  непрерывно дифференцируемы, а функция
непрерывно дифференцируемы, а функция  интегрируема. Тогда существует следующий интеграл и выполняется равенство
интегрируема. Тогда существует следующий интеграл и выполняется равенство
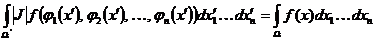 .
.
Полярные координаты
Введем на плоскости полярную систему координат, согласованную с заданной декартовой (  – полярная ось,
– полярная ось,  – расстояние от точки до полюса
– расстояние от точки до полюса  ,
,  – угол между радиусом-вектором точки и полярной осью).
– угол между радиусом-вектором точки и полярной осью).

 |
Данная система уравнений осуществляет преобразование полярных координат в декартовы. Правые части – непрерывно дифференцируемые функции с якобианом
 .
.
Если  ;
;  , то
, то  .
.
Сферические координаты
Пусть заданы полярные координаты в плоскости  ,
,  – угол между радиусом-вектором точки и плоскостью
– угол между радиусом-вектором точки и плоскостью  .
.

 |
Если  ,
,  то
то
 .
.
Цилиндрические координаты
 В плоскости
В плоскости  вводим полярные координаты
вводим полярные координаты  . Тогда координаты
. Тогда координаты  называются цилиндрическими.
называются цилиндрическими.

Эти равенства связывают цилиндрические координаты с декартовыми координатами. Здесь  – расстояние от проекции точки
– расстояние от проекции точки  на плоскость
на плоскость  до начала координат декартовой системы, а
до начала координат декартовой системы, а  – угол между радиусом-вектором указанной проекции и осью
– угол между радиусом-вектором указанной проекции и осью  . Якобиан преобразования легко вычисляется.
. Якобиан преобразования легко вычисляется.
|
|
|
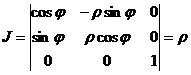 .
.
Если  ;
; 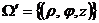 то
то
 .
.
Пример 2.1.11.1. Перейдя к полярным координатам, вычислить двойной интеграл 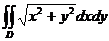 , если
, если  – I четверть круга
– I четверть круга  .
.
Решение.
Полагая  ,
,  имеем
имеем
 .
.
 Пример 2.1.11.2.Вычислить объем тела, ограниченного поверхностями:
Пример 2.1.11.2.Вычислить объем тела, ограниченного поверхностями: 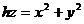 ,
,  .
.
Решение.
Данное тело ограничено снизу параболоидом  , сверху плоскостью
, сверху плоскостью  и проецируется в круг
и проецируется в круг  плоскости
плоскости  . Используем цилиндрические координаты, в которых уравнение параболоида примет вид
. Используем цилиндрические координаты, в которых уравнение параболоида примет вид  . Объем тела равен
. Объем тела равен

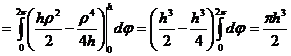 .
.
Пример 2.1.11.3.Вычислить  , если
, если  – шар
– шар  .
.
Решение.
Перейдем к сферическим координатам. В области  координаты
координаты  ,
,  и
и  изменяются так:
изменяются так:  ,
,  ,
,  . Следовательно,
. Следовательно,


 .
.
2.1.12 Потенциальные векторные поля.
Критерии потенциального векторного поля
Потенциальные векторные поля
Пусть дана область  в пространстве
в пространстве  , и
, и  – векторное поле.
– векторное поле.
Определение. Векторное поле называется потенциальным в области  , если существует функция
, если существует функция  такая, что
такая, что
 ,
,  ,
,  ,
,
при этом  называют потенциалом векторного поля
называют потенциалом векторного поля  .
.
Теорема (характеризация потенциальных полей). Рассмотрим векторное поле в некоторой области  . Следующие три условия эквивалентны:
. Следующие три условия эквивалентны:
|
|
|
1) Поле  потенциально.
потенциально.
2) Интеграл от поля  вдоль ориентированной кривой не зависит от начальной и конечной точек этой кривой.
вдоль ориентированной кривой не зависит от начальной и конечной точек этой кривой.
3) Интеграл от векторного поля по любой замкнутой кривой равен нулю.
Пример 2.1.12.1. Показать, что поле  является потенциальным, и найти потенциал этого поля.
является потенциальным, и найти потенциал этого поля.
Решение.
Данное векторное поле определено на всей плоскости  , являющейся односвязной областью. Покажем, что
, являющейся односвязной областью. Покажем, что  , т.е. что поле безвихревое, а следовательно, и потенциальное. Действительно, так как
, т.е. что поле безвихревое, а следовательно, и потенциальное. Действительно, так как
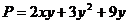 ,
,  ,
,  , то
, то
 .
.
Потенциал  вычислим по формуле
вычислим по формуле
 ,
,
т.е.  .
.
Здесь в качестве начальной точки взята точка  .
.
Формула Грина
Теорема (формула Грина). Пусть в области  задано гладкое векторное поле
задано гладкое векторное поле  , также задано множество
, также задано множество 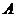 в
в  с кусочно-гладкой границей, которая правильно ориентирована, тогда справедлива следующая формула:
с кусочно-гладкой границей, которая правильно ориентирована, тогда справедлива следующая формула:
 ,
,
где  ,
,  – координаты векторного поля.
– координаты векторного поля.
Пример 2.1.13.1.Применяя формулу Грина, вычислить
 , если
, если  – контур треугольника с вершинами
– контур треугольника с вершинами 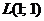 ,
,  ,
,  , пробегаемый против хода часовой стрелки. Проверить результат непосредственным интегрированием.
, пробегаемый против хода часовой стрелки. Проверить результат непосредственным интегрированием.
Решение.
 ,
,  . Находим
. Находим 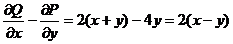 . Таким образом,
. Таким образом,
 , где область
, где область  – треугольник
– треугольник  . Уравнение прямой
. Уравнение прямой  , уравнение
, уравнение 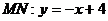 . Вычислим двойной интеграл по данной области:
. Вычислим двойной интеграл по данной области:
|
|
|

 .
.
Вычислим теперь непосредственно криволинейный интеграл по контуру  , состоящему из звеньев
, состоящему из звеньев  ,
,  ,
, 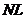 :
:
 .
.
Уравнение  ; следовательно
; следовательно  ,
, 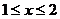 .
.
Уравнение 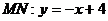 ; следовательно
; следовательно  ,
,  .
.
Уравнение 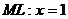 ; значит
; значит 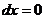 ,
,  .
.
Таким образом,
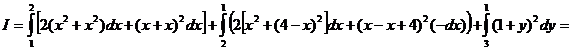
 .
.
Пример 2.1.13.2.Применяя формулу Грина, вычислить  , где
, где  – окружность
– окружность 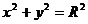 , пробегая против хода часовой стрелки.
, пробегая против хода часовой стрелки.
Решение.
Здесь  ,
,  . Тогда
. Тогда  . Следовательно,
. Следовательно,
 .
.
Дата добавления: 2018-04-15; просмотров: 824; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
