Необходимые и достаточные условия локальных экстремумов
Экстремумы функций многих переменных
Рассмотрим открытое множество  и функцию
и функцию 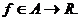
Определение.Точка  называется точкой локального максимума (строгого локального максимума), если существует такое
называется точкой локального максимума (строгого локального максимума), если существует такое  , что для всех векторов
, что для всех векторов 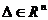 , где
, где  , выполняется неравенство:
, выполняется неравенство:

Определение.Точка  называется точкой локального минимума (строгого локального минимума), если существует такое
называется точкой локального минимума (строгого локального минимума), если существует такое  , что для всех векторов
, что для всех векторов 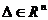 , где
, где  , выполняется неравенство:
, выполняется неравенство:

Определение.Точкой (локального) экстремума называется либо точка максимума, либо точка минимума.
Теорема.Пусть точка 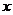 – точка локального экстремума функции
– точка локального экстремума функции 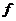 , причем в этой точке существует дифференциал, тогда этот дифференциал равен нулю, то есть
, причем в этой точке существует дифференциал, тогда этот дифференциал равен нулю, то есть  .
.
Определение.Точки, в которых первый дифференциал функции равен нулю, называются критическими (стационарные).
Достаточные условия строгого экстремума
Теорема.Пусть точка 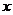 – критическая точка функции
– критическая точка функции 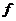 . Допустим, что
. Допустим, что  положительно (отрицательно) определен, тогда функция
положительно (отрицательно) определен, тогда функция 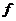 в точке
в точке 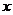 достигает строгого локального минимума (максимума).
достигает строгого локального минимума (максимума).
Пример 2.1.9.1.Найти экстремум функции  .
.
Решение.
Находим частные производные первого порядка:
 ;
;  .
.
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
 откуда
откуда 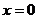 ,
,  ,
,  .
.
Находим значения частных производных второго порядка в точке 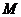 :
:
 ;
;  ;
; 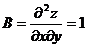 .
.
Составляем дискриминант 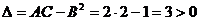 ;
; 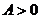 (или
(или  ). Следовательно, в точке
). Следовательно, в точке 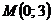 заданная функция имеет минимум. Значение функции в этой точке
заданная функция имеет минимум. Значение функции в этой точке  .
.
|
|
|
Пример 2.1.9.2.Найти экстремум функции
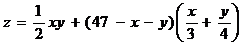 .
.
Решение.
Найдем частные производные первого порядка:
 ;
;  .
.
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
 или
или 
Отсюда  ,
,  ; стационарная точка
; стационарная точка  .
.
Найдем значения вторых производных в точке 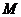 :
:
 .
.
Тогда поскольку  ,
, 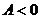 (или
(или  ), то в точке
), то в точке  функция имеет максимум:
функция имеет максимум:  .
.
2.1.10 Задачи на относительный экстремум.
Правило множителей Лагранжа
Постановка задачи на относительный экстремум
Пусть  и заданы функции
и заданы функции  , где
, где  . Рассмотрим задачу нахождения экстремальных значений функции
. Рассмотрим задачу нахождения экстремальных значений функции  при условии, что
при условии, что  , то есть мы учитываем только точки, которые принадлежат множеству
, то есть мы учитываем только точки, которые принадлежат множеству  .
.
Теорема (правило множителей Лагранжа).Пусть в условиях, приведенных выше, функция  достигает своего экстремума при условии, что
достигает своего экстремума при условии, что  . тогда существует ненулевой вектор
. тогда существует ненулевой вектор  такой, что функция
такой, что функция
 ,
,
называемая функцией Лагранжа, в точке x имеет градиент, равный нулю:
 .
.
Теорема.Достаточное условие относительного локального экстремума. Пусть 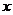 является критической точкой для функции Лагранжа в задаче на относительный экстремум, то есть
является критической точкой для функции Лагранжа в задаче на относительный экстремум, то есть 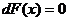 и
и  Рассмотрим
Рассмотрим  – множество приращений, которые удовлетворяют уравнениям
– множество приращений, которые удовлетворяют уравнениям
|
|
|
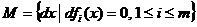 .
.
Если второй дифференциал функции Лагранжа является положительно (отрицательно) определимым на множестве 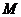 , то точка
, то точка 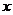 является точкой локального минимума (максимума) в задаче на относительный экстремум.
является точкой локального минимума (максимума) в задаче на относительный экстремум.
Пример 2.1.10.1.Найти экстремум функции  при условии, что
при условии, что 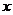 и
и  связаны уравнением
связаны уравнением  .
.
Решение.
Рассмотрим функцию Лагранжа 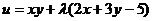 . Имеем
. Имеем  ,
,  . Из системы уравнений (необходимые условия экстремума)
. Из системы уравнений (необходимые условия экстремума)

Находим  ,
,  ,
,  . Нетрудно видеть, что в точке
. Нетрудно видеть, что в точке  функция
функция  достигает наибольшего значения
достигает наибольшего значения  .
.
Пример 2.1.10.2.Найти наименьшее и наибольшее значения функции  в круге
в круге  .
.
Решение.
Здесь рассматривается область  , ограниченная окружностью
, ограниченная окружностью  , включая и точки окружности.
, включая и точки окружности.
Найдем стационарные точки данной функции; имеем  ,
,  ; в силу необходимых условий экстремума находим
; в силу необходимых условий экстремума находим 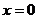 ,
,  .
.
Нетрудно видеть, что в точке  функция
функция  имеет наименьшее значение
имеет наименьшее значение  , причем указанная точка является внутренней точкой области
, причем указанная точка является внутренней точкой области  .
.
Исследуем на условный экстремум функцию  , если
, если 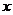 и
и  связаны соотношением
связаны соотношением  . Рассмотрим функцию
. Рассмотрим функцию  . Находим частные производные
. Находим частные производные 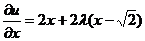 ,
, 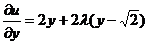 . Для определения
. Для определения 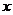 ,
,  и
и 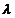 получаем систему уравнений
получаем систему уравнений

Эта система имеет два решения:  ,
,  и
и  ;
;  ,
,  и
и  . Значит, наибольшее значение функция принимает в точке
. Значит, наибольшее значение функция принимает в точке  . Итак,
. Итак,  ,
,  .
.
|
|
|
2.1.11 Теорема о замене переменных в кратных интегралах.
Полярные, цилиндрические и сферические системы координат.
Геометрический смысл Якобиана
Дата добавления: 2018-04-15; просмотров: 358; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
