Математическое моделирование, математическое программирование, теория игр, численные методы
1. Регрессионная модель. Однофакторная модель (построение модели, определение дисперсии, проверка адекватности).
2. Двойственная задача линейного программирования.
3. Производственная функция Кобба-Дугласа. Коэффициенты эластичности.
4. Модели расчета годовой производственной программы. Критерии в моделях.
5. Модель оптимальной загрузки оборудования для выпуска комплектной продукции. Виды комплектов.
6. Математическая обработка результатов опытов в планировании эксперимента. Полный факторный эксперимент. Свойства матрицы планирования.
7. Управление запасами материалов. Типы моделей. Простейшая модель Уилсона.
8. Сетевые графики. Критический путь. Оптимизация графика по времени в зависимости от вложенных средств.
9. Сетевые графики. Вероятностная сеть. Оценка времени выполнения работ.
10. Динамическое программирование. Распределение ресурсов между предприятиями головной фирмы.
11. Задачи раскроя материалов и составления смеси. Область применения.
12. Транспортная задача. Закрытая транспортная задача.
13. Открытая транспортная задача.
14. Матричные игры. Игры  и
и  .
.
15. Матричные игры 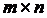 и линейное программирование.
и линейное программирование.
16. Методы решения нелинейных уравнений.
17. Методы решения систем линейных уравнений.
18. Нахождение наибольшего по модулю собственного числа матрицы.
19. Полиномиальное интерполирование.
20. Метод наименьших квадратов.
21. Численное интегрирование.
|
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВОПРОСАМ ПРОГРАММЫ
Математический анализ
Теоремы Вейерштрасса
Функции, непрерывные на отрезке
Рассмотрим числовую функцию 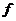 , заданную на отрезке
, заданную на отрезке  . Будем говорить, что она непрерывна на этом отрезке, если она непрерывна в каждой точке из области определения (на концах отрезка требуется односторонняя непрерывность).
. Будем говорить, что она непрерывна на этом отрезке, если она непрерывна в каждой точке из области определения (на концах отрезка требуется односторонняя непрерывность).
Отметим некоторые специфические свойства непрерывных функций на отрезке.
Теорема (первая теорема Вейерштрасса).Если функция 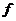 непрерывна на отрезке
непрерывна на отрезке  , то она ограничена на нем.
, то она ограничена на нем.
Теорема (вторая теорема Вейерштрасса).Если функция 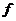 непрерывна на отрезке
непрерывна на отрезке  , то она достигает своих наибольшего и наименьшего значений на нем, т.е. существуют точки
, то она достигает своих наибольшего и наименьшего значений на нем, т.е. существуют точки  и
и  на отрезке
на отрезке  такие, что для любого
такие, что для любого  справедливо неравенство
справедливо неравенство  .
.

 Пример 2.1.1.1.Найти наибольшее и наименьшее значения функции
Пример 2.1.1.1.Найти наибольшее и наименьшее значения функции 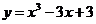 на отрезке
на отрезке  .
.
Решение.
Так как  , то критическими точками функции являются
, то критическими точками функции являются  и
и  . Сравниваем значения функции в этих точках и значения функции на концах заданного отрезка:
. Сравниваем значения функции в этих точках и значения функции на концах заданного отрезка:
 ;
;  ;
;  ;
;  .
.
Отсюда наименьшее значение функции  достигается в точке
достигается в точке  (в точке минимума), а наибольшее
(в точке минимума), а наибольшее 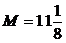 достигается в точке
достигается в точке  (на правом конце отрезка).
(на правом конце отрезка).
|
|
|
Теоремы Роля, Лагранжа
Теорема Ролля.Пусть функция 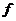 непрерывна на отрезке
непрерывна на отрезке  , имеет производную на интервале
, имеет производную на интервале  и принимает равные значения на его концах
и принимает равные значения на его концах  . Тогда на интервале
. Тогда на интервале  существует, по крайней мере, одна точка
существует, по крайней мере, одна точка  , в которой производная зануляется
, в которой производная зануляется  .
.
Теорема Лагранжа.Пусть функция 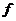 непрерывна на отрезке
непрерывна на отрезке  , имеет производную на интервале
, имеет производную на интервале  . Тогда на интервале
. Тогда на интервале  существует точка
существует точка  , для которой выполняется равенство
, для которой выполняется равенство  .
.
Теорема Лагранжа имеет простой геометрический смысл. Действительно,  есть тангенс угла наклона секущей, проходящей через точки
есть тангенс угла наклона секущей, проходящей через точки  и
и  , а
, а  – тангенс угла наклона касательной в точке
– тангенс угла наклона касательной в точке  , следовательно, рассматриваемые секущая и касательная параллельны.
, следовательно, рассматриваемые секущая и касательная параллельны.
Пример 2.1.2.1.Показать, что функция 
 на отрезках
на отрезках  и
и  удовлетворяет условиям теоремы Ролля. Найти соответствующие значения
удовлетворяет условиям теоремы Ролля. Найти соответствующие значения  .
.
Решение.
Функция  непрерывна и дифференцируема для всех значений
непрерывна и дифференцируема для всех значений  ; кроме того,
; кроме того,  . Следовательно, теорема Ролля применима на отрезках
. Следовательно, теорема Ролля применима на отрезках  и
и  . Для нахождения числа
. Для нахождения числа  составляем уравнение:
составляем уравнение:  . Отсюда
. Отсюда 
 причем
причем  ;
;  .
.
Пример 2.1.2.2. Проверить выполнение теоремы Лагранжа для функции  на отрезке
на отрезке  и найти соответствующее промежуточное значение
и найти соответствующее промежуточное значение  .
.
Решение.
Функция  непрерывна и дифференцируема для всех значений
непрерывна и дифференцируема для всех значений 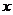 , причем
, причем  . Отсюда по формуле Лагранжа имеем,
. Отсюда по формуле Лагранжа имеем,  т. е.
т. е.  .
.
|
|
|
Следовательно,  и
и  ; подходит только значение
; подходит только значение  , для которого справедливо неравенство
, для которого справедливо неравенство 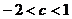 .
.
Теоремы Коши, Ферма
Теорема Коши.Пусть функции 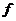 и
и  непрерывны на отрезке
непрерывны на отрезке  , имеют производные
, имеют производные  и
и  на интервале
на интервале  одновременно не обращающиеся в
одновременно не обращающиеся в 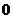 ,
,  . Тогда на интервале
. Тогда на интервале  существует точка
существует точка  , для которой выполняется равенство
, для которой выполняется равенство  .
.
Теорема Ферма.Пусть функция 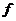 достигает в точке
достигает в точке  локального экстремума (максимума или минимума) и в ней существует производная, тогда
локального экстремума (максимума или минимума) и в ней существует производная, тогда  .
.
Пример 2.1.3.1. Для функции  и
и  проверить выполнение условий теоремы Коши на отрезке
проверить выполнение условий теоремы Коши на отрезке  и найти
и найти  .
.
Решение.
Проверим выполнение условий теоремы Коши. Функции  и
и  непрерывны на отрезке
непрерывны на отрезке  и при
и при  имеют производные, не обращающиеся в нуль одновременно, причем
имеют производные, не обращающиеся в нуль одновременно, причем  .
.
Тогда по теореме Коши
 или
или  . Отсюда
. Отсюда  , где
, где  .
.
Пример 2.1.3.2. Для функции 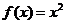 проверить выполнение условий теоремы Ферма.
проверить выполнение условий теоремы Ферма.
Решение.
Очевидно, функция  имеет минимум в точке
имеет минимум в точке 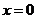 . Так как
. Так как  , то
, то  , как и утверждает теорема Ферма.
, как и утверждает теорема Ферма.
Формула Тейлора
Основным свойством дифференциального исчисления является формула Тейлора, позволяющая приближать функции специальными многочленами в окрестности некоторой точки. Мы рассмотрим формулу Тейлора с остаточным членом в форме Лагранжа (глобальная формула Тейлора) и с остаточным членом в форме Пеано (локальная формула Тейлора).
|
|
|
Пусть функция 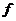 в некотором интервале
в некотором интервале  имеет
имеет  производных, тогда для любой точки
производных, тогда для любой точки  можно написать многочлен Тейлора
можно написать многочлен Тейлора
 .
.
Разность  называется остаточным членом формулы Тейлора, это выражение может быть преобразовано различными способами, которые приводят к разным формам остаточного члена.
называется остаточным членом формулы Тейлора, это выражение может быть преобразовано различными способами, которые приводят к разным формам остаточного члена.
Теорема (остаточный член в форме Пеано).Пусть функция 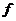 в некотором интервале
в некотором интервале  имеет
имеет  непрерывных производных, тогда для любой точки
непрерывных производных, тогда для любой точки  при
при  имеет место равенство:
имеет место равенство:
 .
.
Теорема (остаточный член в форме Лагранжа).Пусть функция 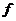 в некотором интервале
в некотором интервале  , содержащем точку
, содержащем точку  , имеет
, имеет  производных, а во всех точках этого интервала, кроме, быть может, точки
производных, а во всех точках этого интервала, кроме, быть может, точки  , имеет
, имеет  -ю производную; тогда для любого
-ю производную; тогда для любого  ,
, 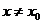 существует
существует 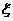 , находящееся между
, находящееся между  и
и 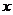 , для которой выполнено равенство:
, для которой выполнено равенство:
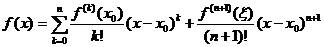 .
.
Заметим, что при 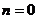 последняя теорема превращается в теорему Лагранжа.
последняя теорема превращается в теорему Лагранжа.
Формулу Тейлора в точке  обычно называют формулой Маклорена. В этом случае удобно положить
обычно называют формулой Маклорена. В этом случае удобно положить  , т.е.
, т.е. 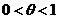 .
.
Пример 2.1.4.1. Разложить по формуле Маклорена функцию  .
.
Решение.
 ,
,
 ,
,
…
 .
.
Тогда  ,
,  и так как
и так как  , то
, то  ,
, 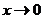 .
.
Пример 2.1.4.2. Функцию  разложить по степеням бинома
разложить по степеням бинома 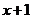 до члена, содержащего
до члена, содержащего  .
.
Решение.
 для всех
для всех  ,
,  . Следовательно,
. Следовательно,
 , где
, где  ,
, 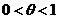 .
.
Длина гладкой кривой
Рассмотрим некоторую функцию  . Для фиксированного значения
. Для фиксированного значения  – есть некоторая точка
– есть некоторая точка  в
в  . Такую функцию называют параметрическим представлением кривой
. Такую функцию называют параметрическим представлением кривой  в пространстве
в пространстве  (роль параметра играет переменная
(роль параметра играет переменная  ). Кривая
). Кривая  называется непрерывной (соответственно гладкой), если все функции
называется непрерывной (соответственно гладкой), если все функции  являются непрерывными (соответственно непрерывно дифференцируемыми). Пусть
являются непрерывными (соответственно непрерывно дифференцируемыми). Пусть  – некоторое разбиение отрезка
– некоторое разбиение отрезка  ; рассмотрим точки
; рассмотрим точки  и ломаную
и ломаную  , которая получается последовательным соединением точек
, которая получается последовательным соединением точек  и
и  прямолинейными отрезками. Такие ломаные называют вписанными в кривую
прямолинейными отрезками. Такие ломаные называют вписанными в кривую  . Пусть
. Пусть 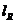 – длина ломаной
– длина ломаной  .
.

Кривая называется спрямляемой, если конечна величина  , где верхняя грань берется по всем вписанным в
, где верхняя грань берется по всем вписанным в  ломаным. За значение длины кривой
ломаным. За значение длины кривой 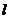 как раз и принимают указанную величину.
как раз и принимают указанную величину.
Оказывается, что для гладких кривых существует достаточно простой способ вычисления длинны 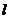 .
.
Теорема: Гладкая кривая является спрямляемой, причем для ее длины 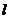 справедлива следующая формула:
справедлива следующая формула:
 .
.
 Пример 2.1.5.1. Найти длину астроиды
Пример 2.1.5.1. Найти длину астроиды  .
.
 Решение.
Решение.
Дифференцируя уравнение астроиды, получим  , отсюда
, отсюда  .
.
Поэтому для длины дуги одной четверти астроиды имеем:
 .
.
Отсюда 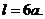
 Пример 2.1.5.2. Найти длину одной арки циклоиды
Пример 2.1.5.2. Найти длину одной арки циклоиды 

Решение.
Имеем  и
и  . Поэтому
. Поэтому
 .
.
Пределы интегрирования  и
и  соответствуют крайними точкам арки циклоиды.
соответствуют крайними точкам арки циклоиды.

 Пример 2.1.5.3. Найти всю длину кардиоиды
Пример 2.1.5.3. Найти всю длину кардиоиды  .
.
Решение.
В силу симметрии кривой найдем сначала половину длины. Поскольку  , получим:
, получим:

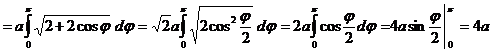 .
.
Отсюда 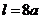 .
.
Объем тела вращения
Пусть  – кривая, описываемая в декартовой системе координат на плоскости непрерывной неотрицательной функцией
– кривая, описываемая в декартовой системе координат на плоскости непрерывной неотрицательной функцией 
 . Рассмотрим формулу для вычисления
. Рассмотрим формулу для вычисления  – объема тела вращения, ограниченного плоскостями
– объема тела вращения, ограниченного плоскостями  и
и  и поверхностью вращения кривой
и поверхностью вращения кривой  вокруг оси
вокруг оси  в трехмерном пространстве.
в трехмерном пространстве.
Теорема. Для величины  справедлива следующая формула:
справедлива следующая формула:
 .
.
 Пример 2.1.6.1. Найти объем тела, образованного вращением вокруг оси
Пример 2.1.6.1. Найти объем тела, образованного вращением вокруг оси  фигуры, ограниченной кривой
фигуры, ограниченной кривой  и прямой
и прямой  .
.
Решение.
 .
.
Пример 2.1.6.2. Вычислить объем тела, образованного вращением фигуры, ограниченной одной полуволной синусоиды  и отрезком
и отрезком  оси
оси 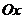 вокруг оси
вокруг оси  .
.

Решение.
Воспользуемся формулой  . Тогда
. Тогда

 .
.
Пример 2.1.6.3. Вычислить объем тела, полученного вращением вокруг оси 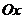 одной арки циклоиды
одной арки циклоиды  ,
, 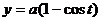
 .
.
Решение:

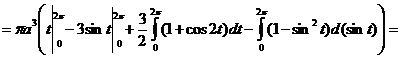
 .
.
 Пример 2.1.6.4. Определить объем, образованный вращением кривой
Пример 2.1.6.4. Определить объем, образованный вращением кривой  вокруг полярной оси.
вокруг полярной оси.
Решение.
Воспользуемся формулой  .
.

 .
.
Дата добавления: 2018-04-15; просмотров: 331; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
