Тема 8. Характеристические числа графов
Цикломатическим числом графа G называется число ребер, которые надо убрать, что бы граф стал ацикличным.
Цикломатическое число графа G находится по формуле:
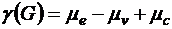, (8.1)
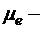число вершин,
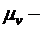число ребер,
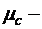число компонент связности.
Замечание. Если цикломатическое число графа равно 1, то в графе ровно 1 цикл.
Внутренне устойчивым множеством графа G называется множество вершин S, все вершины которого попарно несмежны.
Число внутренней устойчивости:
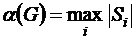. (8.2)
Внешне устойчивым множеством графа G называется множество вершин Q, таких, что из всех вершин множества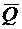 
ведут ребра в вершины множества Q.
Число внутренней устойчивости:
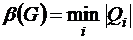. (8.3)
Граф G называется h-хроматическим, если его вершины можно раскрасить h различными красками так, чтобы никакие две смежные (различные) вершины не были окрашены в один цвет. Хроматическое число графа– это наименьшее число красок.
.
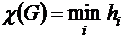Граф G называется k-раскрашиваемым, если его ребра можно раскрасить k различными красками так, чтобы никакие два смежных ребра не были окрашены в один цвет. Хроматический индекс графа – это наименьшее число красок.
.
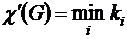Согласно теореме Визинга, если максимальная локальная степень вершины графа равна k, то хроматический индекс подчиняется условию:
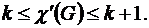
Пример 8.1.
Для графа, приведенного на рисунке 8.1, найти все характеристические числа.
|
|
|
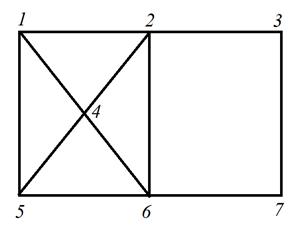
Рис. 8.1. Нахождение характеристических чисел графа
Решение:
Характеристическими числами графа называются:
1) цикломатическое число, 2) число внутренней устойчивости, 3) число внешней устойчивости, 4) хроматическое число, 5) хроматический индекс.
1) Для нахождения цикломатического числа необходимо выяснить, сколько ребер графа достаточно убрать, чтобы разрушить все существующие циклы. Из рисунка 8.2 видно, что таких ребер минимум 5. Они указаны пунктиром.
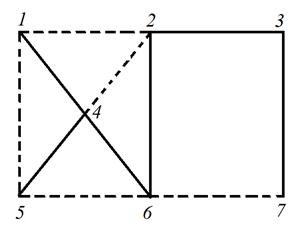
Рис. 8.2. Нахождение цикломатического числа графа
Этот же результат можно получить по формуле (8.1).
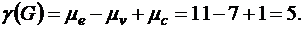
Здесь 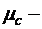число компонент связности графа. Так как все вершины графа связны (связаны маршрутами), то у этого графа 1 компонента связности.
2) Для нахождения числа внутренней устойчивости, необходимо выяснить, каким будет максимальное внутренне устойчивое множество графа.
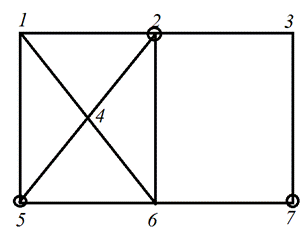
Рис. 8.3. Нахождение числа внутренней устойчивости графа
Для этого надо определить максимальную совокупность попарно несмежных вершин. Из рисунка 8.3 видно, что таких вершин максимум 3. Они помечены кружком.
Таким образом, максимальным внутренне устойчивым множеством будут множества вершин S1 = {2, 5, 7}, S2 = {1, 6, 3}.
Тогда по формуле (8.2) получим число внутренней устойчивости:
|
|
|
.
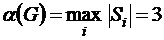3) Для нахождения числа внешней устойчивости, необходимо выяснить, каким будет минимальное внешне устойчивое множество графа.
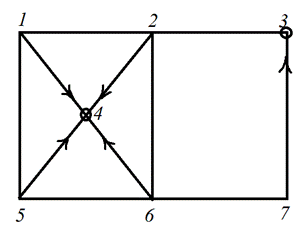
Рис. 8.4. Нахождение числа внешней устойчивости графа
На рисунке 8.4 видно, что вершины множества Q1 = {4, 3} таковы, что из остальных вершин графа, составляющих множество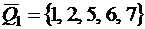 
, ведут ребра в вершины 4 или 3. Значит множество Q1 – это множество внешней устойчивости. Очевидно, что таким же свойством обладает множество Q2 = {4, 7}. Оба этих множества минимальны, то есть множества из одной вершины, обладающего указанным свойством, найти нельзя.
Тогда по формуле (8.3) получим число внешней устойчивости:
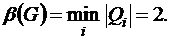
4) Для нахождения хроматического числа, необходимо выяснить, каким будет минимальное количество красок, в которые можно раскрасить вершины графа, так чтобы никакие две смежные вершины не были окрашены в один цвет.
Для этого надо определить внутренне устойчивые множества графа с как можно большей мощностью.
На рисунке 8.5 видно, что вершины 2, 5 и 7 – попарно несмежны, значит, их можно раскрасить в один и тот же цвет (например, красный). Он помечен звездочками.
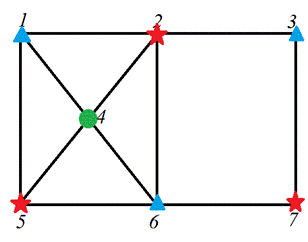
Рис. 8.5. Нахождение хроматического числа графа
|
|
|
Далее, множество несмежных вершин составляют вершины 1, 6 и 3. Значит, они тоже могут быть раскрашены в один цвет (например, голубой). Он помечен треугольниками.
Очевидно, что вершину 4 нельзя раскрасить ни в красный, ни в голубой цвета. Для нее придется использовать третий цвет (например, зеленый). Он помечен кружком.
Таким образом, минимальное количество цветов – 3. Значит хроматическое число графа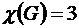 
.
5) Для нахождения хроматического индекса, необходимо выяснить, каким будет минимальное количество красок, в которые можно раскрасить ребра графа, так чтобы никакие два смежных ребра не были окрашены в один цвет.
Воспользуемся теоремой Визинга. Найдем число k – максимальное количество ребер, инцидентных одной и той же вершине.
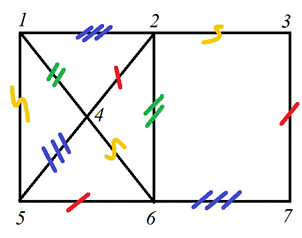
Рис. 8.6. Нахождение хроматического индекса графа
На рисунке 8.6 видно, что вершина 4 имеет самое большое из всех количество инцидентных ребер. Поэтому k = 4.
Тогда по теореме Визинга хроматический индекс подчиняется условию:
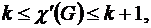
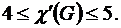
Осталось определить, достаточно ли четырех цветов для указанной раскраски ребер, или потребуется пять.
Возьмем вершину 4 и раскрасим все инцидентные ей ребра в разные цвета. Например, в красный, зеленый, синий и желтый. На рисунке 8.6 они помечены соответственно одной чертой, двумя чертами, тремя чертами и волной.
|
|
|
Далее, распределяем указанные цвета на оставшихся не раскрашенными ребрах, учитывая то, что смежные ребра не могут быть окрашены в один цвет.
В итоге, мы сумели обойтись четырьмя цветами, значит, хроматический индекс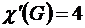 
.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Дата добавления: 2018-04-15; просмотров: 1304; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!