Теорема (о мощности прямого произведения множеств).
Федеральное государственное бюджетное образовательное учреждение высшего образования
«КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Кафедра прикладной математики
Методические указания
Для выполнения контрольных работ по
ДИСКРЕТНОЙ МАТЕМАТИКЕ
Часть
Кемерово
2017
© С. Г. Гутова, 2017
© Кемеровский государственный
университет, 2017
ISBN 978-5-8353-1686-1
Об издании – 1, 2, 3
ББК Ю25я73
УДК 519.6
Г 89
Издается по решению редакционно-издательского совета
Кемеровского государственного университета
Составитель:
Гутова Светлана Геннадьевна – кандидат технических наук, доцент кафедры АИТК
Г 89 Гутова, С. Г. Методические указания для выполнения контрольных работ по дискретной математике. 1 часть:электронное учебно-методическое пособие: тексто-графические учебные материалы [Электронный ресурс]: / С. Г. Гутова; КемГУ. – Электрон. дан. (1 Мб). – Кемерово: КемГУ, 2017. – 1 электрон. опт. диск (СD-ROM). – Систем. требования: Intel Pentium (или аналогичный процессор других производителей), 500 МГц; 512 Мб оперативной памяти; видеокарта SVGA, 1280x1024 High Color (32 bit); 2 Мб свободного дискового пространства; операц. система Windows ХР/7/8; Adobe Reader. – Загл. с экрана. – Номер гос. регистрации в ФГУП НТЦ «Информрегистр» __________ свид. № _____ от __.__.____.
ISBN 978-5-8353-1686-1
Учебно-методическое пособие разработано по дисциплине «Дискретная математика» для направления 01.03.02 «Прикладная математика и информатика» в соответствии с требованиями ФГОС ВО и включает краткий теоретический материал, примеры решения задач, методические рекомендации. Может быть использовано для выполнения контрольных работ по дисциплине «Дискретная математика» студентами направлений 02.03.02 «Фундаментальная информатика и информационные технологии» и 02.03.03 «Математическое обеспечение и администрирование информационных систем» и по дисциплине «Дискретная математика и математическая логика» студентами направления 02.03.01 «Математика и компьютерные науки». Предназначено для студентов 1-2 курсов заочной формы обучения института фундаментальных наук.
|
|
|
| Утверждено на заседании кафедры прикладной математики Протокол № 7 от «20 » февраля 2017 г. Заведующий кафедрой, ____________________ Е. С. Каган | Рекомендовано научно-методическим советом института фундаментальных наук Рекомендовано «__»________________2018 г. Председатель совета доцент _____________С. М. Сирик |
© С. Г. Гутова, 2017
© Кемеровский государственный
университет, 2017
Текстовое электронное издание
Минимальные системные требования:
Компьютер: Pentium 3 и выше, 500 МГц; ОЗУ 512 Мб; 2 Мб на жестком диске; видеокарта SVGA, 1280x1024 High Color (32 bit); привод
CD-ROM
Операционная система: Windows ХР/7/8
|
|
|
Программное обеспечение: Adobe Reader
Номер государственной регистрации электронного издания __________.
© С. Г. Гутова, 2017
© Кемеровский государственный
университет, 2017
Оглавление
ГЛАВА 1. ТЕОРИЯ МНОЖЕСТВ. 5
Тема 1. Множества. 5
Тема 2. Векторы и прямые произведения множеств. Проекция вектора на ось 12
Тема 3. Комбинаторика. 17
Тема 4. Соответствия. 29
Тема 5. Отношения. 36
ГЛАВА 2. ТЕОРИЯ ГРАФОВ.. 44
Тема 6. Способы задания графов. Локальные степени вершин. 44
Тема 7. Маршруты. Расстояние между вершинами графа. Диаметр и центр графа 51
Тема 8. Характеристические числа графов. 55
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.. 60
1. Индивидуальные задания по теме «Множества». 60
2. Индивидуальные задания по теме «Векторы и прямые произведения множеств. Проекция вектора на ось». 63
3. Индивидуальные задания по теме «Комбинаторика». 65
4. Индивидуальные задания по теме «Соответствия». 67
5. Индивидуальные задания по теме «Отношения». 68
6. Индивидуальные задания по теме «Способы задания графов. Локальные степени вершин». 71
7. Индивидуальные задания по теме «Маршруты. Расстояние между вершинами графа. Диаметр и центр графа». 75
|
|
|
8. Индивидуальные задания по теме «Характеристические числа графов» 78
Литература. 81
ГЛАВА 1. ТЕОРИЯ МНОЖЕСТВ.
Тема 1. Множества
Множество — один из ключевых объектов математики, в частности, теории множеств. «Множество есть многое, мыслимое нами как единое», говорил Георг Кантор (1845-1918). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением
Множество можно представить как совокупность некоторых объектов, объединенных по какому-либо признаку.
Множество состоит из элементов. В зависимости от их числа множества различают как конечные или бесконечные. Конечные множества могут состоять из одного или нескольких элементов.
Мощность множества – количество его элементов. Мощность множества М обозначается так:  .
.
Множество, не содержащее элементов, называется пустым множеством и обозначается Æ.
Множество обозначают заглавными буквами, а его элементы – прописными. Для записи множества используют фигурные скобки. Например, множество натуральных чисел от 3 до 10: М = {3, 4, 5, 6, 7, 8, 9, 10}.
Говоря об определенном множестве, мы полагаем, что для каждого объекта имеется две возможности: либо он входит в рассматриваемое множество, т.е. является его элементом, принадлежит ему (обозначается  ); либо нет (обозначается
); либо нет (обозначается  ).
).
|
|
|
Способы задания множества:
- перечисление всех элементов множества, например, множество однозначных неотрицательных чисел X = {0, 1, 2, 3, …, 9};
- указание общего свойства, которым обладают все элементы множества, например, множество четных натуральных чисел X = {2, 4, 6, 8, 10, 12, …} или X = {x: x = 2n, 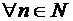 };
};
- рекуррентно, например:  ,
,  и др.
и др.
Множество А называют подмножеством множества В (обозначается  ), если каждый элемент множества А является также элементом множества В.
), если каждый элемент множества А является также элементом множества В.
Множества А и В называют равными (  ), если каждый элемент множества А является одновременно элементом множества В и наоборот, т.е. если
), если каждый элемент множества А является одновременно элементом множества В и наоборот, т.е. если  и
и  . Другими словами, два множества равны, если они состоят из одних и тех же элементов. Если
. Другими словами, два множества равны, если они состоят из одних и тех же элементов. Если  , но при этом
, но при этом  , то А называется строгим (или собственным) подмножеством В.
, то А называется строгим (или собственным) подмножеством В.
На рисунке 1.1 приведена диаграмма Эйлера-Вьенна, где видно, что множество А целиком содержится в множестве В.

Рис. 1.1. Множество А – строгое подмножество В
Заметим, что контуры на данном рисунке могут иметь любую форму. Чаще всего используются окружности. Поэтому диаграмму Эйлера-Вьенна иначе называют – круги Эйлера.
Множество U называется универсальным множеством (множество всех подмножеств) для некоторой системы множеств, если каждое множество этой системы является подмножеством U, то есть {A, B, C, …}:  ,
,  ,
,  , …
, …
Дополнением множества А называется множество  , состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
На рисунке 1.2 приведена диаграмма, где темным цветом выделено множество  .
.

Рис.1.2. Дополнение множества А
Пересечением двух множеств А и В называется множество  , состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
На рисунке 1.3 приведены круги Эйлера, где темным цветом выделено пересечение множеств А и В.

Рис. 1.3. Пересечение множеств А и В
Объединением двух множеств А и В называется множество 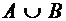 , состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно, то есть хотя бы одному из них.
, состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно, то есть хотя бы одному из них.
На рисунке 1.4 приведены круги Эйлера, где темным цветом выделено объединение множеств А и В.

Рис. 1.4. Объединение множеств А и В
Разностью двух множеств А и В называется множество  (или
(или 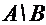 ), состоящее из тех элементов множества А , которые не принадлежат множеству В:
), состоящее из тех элементов множества А , которые не принадлежат множеству В:
 .
.
На рисунке 1.5 приведены круги Эйлера, где темным цветом выделена разность множеств А и В.

Рис. 1.5. Разность множеств А и В
Пример 1: Заданы два множества: А = {-2, -1, 0, 1, 2} и B = {0, 2, 4, 5}. Определить множества  ;
;  ;
; 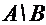 ;
;  и их мощность.
и их мощность.
Решение:
Множество А = {-2, -1, 0, 1, 2} состоит из пяти элементов, следовательно мощность этого множества равна 5:  .
.
Аналогично, B = {0, 2, 4, 5} содержит 4 элемента:  .
.
По определению пересечение двух множеств состоит только из общих для обоих множеств элементов, следовательно,  {0, 2} и
{0, 2} и  .
.
По определению объединение двух множеств состоит из всех элементов, которые принадлежат только множеству А, или только множеству В, или множествам А и В одновременно, следовательно, 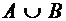 = {-2, -1, 0, 1, 2, 4, 5} и
= {-2, -1, 0, 1, 2, 4, 5} и  .
.
Множество 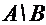 является разностьюдвух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно
является разностьюдвух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно  {-2, -1, 1} и
{-2, -1, 1} и  .
.
Аналогично,  {4, 5} и
{4, 5} и  .
.
Пример 2:
Дано универсальное множество U = 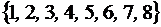 ;
;
множества А =  ; В =
; В =  ; С =
; С =  .
.
Найти:  . Записать ответ в виде списка.
. Записать ответ в виде списка.
Решение:
Решаем по действиям.
1) Найдем 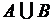 . Это множество элементов, которые принадлежат либо А, либо В, либо А и В одновременно. Это означает, что надо составить общий список элементов этих множеств. Так как порядок элементов в множестве произвольный, то при получения объединения А и В сначала выпишем все элементы множества А, затем добавим те элементы множества В, которые еще не встречались. Удобно переобозначить это множество одной буквой, например D.
. Это множество элементов, которые принадлежат либо А, либо В, либо А и В одновременно. Это означает, что надо составить общий список элементов этих множеств. Так как порядок элементов в множестве произвольный, то при получения объединения А и В сначала выпишем все элементы множества А, затем добавим те элементы множества В, которые еще не встречались. Удобно переобозначить это множество одной буквой, например D.
 .
.
2) Найдем множество  . Для этого выпишем те элементы множества U, которые не принадлежат С. Так 1 принадлежит С, значит ее не включаем в
. Для этого выпишем те элементы множества U, которые не принадлежат С. Так 1 принадлежит С, значит ее не включаем в  , 2 – принадлежит С, значит ее не включаем в
, 2 – принадлежит С, значит ее не включаем в  , 3 – не принадлежит С, значит ее включаем в
, 3 – не принадлежит С, значит ее включаем в  , и так далее.
, и так далее.
 .
.
3) Найдем  . Это множество элементов принадлежащих одновременно D и
. Это множество элементов принадлежащих одновременно D и  . Для этого будем брать по очереди элементы D и проверять их наличие в множестве
. Для этого будем брать по очереди элементы D и проверять их наличие в множестве  . Если элемент есть в обоих множествах, включаем его в
. Если элемент есть в обоих множествах, включаем его в  . Например,
. Например,  , но
, но  , значит 1 не включаем в искомое пересечение. Далее,
, значит 1 не включаем в искомое пересечение. Далее, 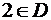 , но
, но  , значит 2 не включаем в искомое пересечение;
, значит 2 не включаем в искомое пересечение; 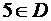 и
и  , значит 5 включаем в искомое пересечение; и так далее.
, значит 5 включаем в искомое пересечение; и так далее.
 .
.
Пример 3:
На диаграмме Вьенна-Эйлера изобразить результат действия
 .
.
Решение:
Решаем по действиям. На каждой копии диаграммы необходимо восстановить контуры всех множеств, участвующих в задании. Они должны пересекаться в самом общем виде. Самый большой контур – универсальное множество. Оно содержит в себе все множества задачи. На рисунке 1.6 приведена такая диаграмма для данного примера. Это основа диаграммы для выполнения каждого действия.

Рис.1.6. Основа диаграммы для трех множеств
1) Изобразим на 1 диаграмме множества, вступающие в 1 действие (действие в скобках). Каждое множество заштриховываем штриховкой своего вида (с наклоном влево, с наклоном вправо, горизонтальной или вертикальной). Множества штрихуются целиком, независимо от их пересечения с другими множествами диаграммы.
На рисунке 1.7 видно, что в результате получилось четыре вида штриховки: левая, правая, двойная и пустая (нет штриховки).
Так как первое действие – разность  , из всех видов штриховки надо выбрать ту одинарную штриховку, которая соответствует множеству А. То есть отбросить ту часть множества А, которая покрыта двойной штриховкой, так как она одновременно является частью множества В. Эту часть мы переносим на 2 копию диаграммы в качестве результата 1 действия.
, из всех видов штриховки надо выбрать ту одинарную штриховку, которая соответствует множеству А. То есть отбросить ту часть множества А, которая покрыта двойной штриховкой, так как она одновременно является частью множества В. Эту часть мы переносим на 2 копию диаграммы в качестве результата 1 действия.

Рис.1.7. Множества, вступающие в 1 действие
2) На 2 копии диаграммы (см. рис. 1.8) надо заштриховать множества, вступающие во второе действие, то есть  и С.
и С.

Рис.1.8. Множества, вступающие во 2 действие
Так как второе действие – пересечение  , то из всех видов штриховки надо выбрать двойную штриховку, которая соответствует общей части множеств D и C. Эту часть мы переносим на 3 копию диаграммы в качестве результата 2 действия, то есть ответа (см. рис. 1.9).
, то из всех видов штриховки надо выбрать двойную штриховку, которая соответствует общей части множеств D и C. Эту часть мы переносим на 3 копию диаграммы в качестве результата 2 действия, то есть ответа (см. рис. 1.9).

Рис.1.9. Ответ
Заметим, что на каждой копии диаграммы, кроме последней, должно быть ровно два вида штриховки, а на последней копии – один.
Тема 2. Векторы и прямые произведения множеств.
Проекция вектора на ось
Вектор – это упорядоченный набор элементов (“кортеж”). Его элементы зазываются координатами или компонентами вектора.
Длина (размерность) вектора – число координат вектора.
В отличие от элементов множества, его координаты могут совпадать. Обозначение вектора – в круглых скобках, координаты – через запятую (0, 5, 4, 5, 0, 1). Иногда скобки и даже запятые опускаются. Тогда вектор называют словом: 054501.
Векторы длины 2 называют упорядоченными парами; длины 3 – тройками; и так далее, длины n – n-ками.
Два вектора равны, если они имеют одинаковую длину, и соответствующие координаты равны, то есть 
 , если
, если 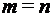 и
и 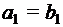 ,
, 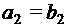 , …,
, …,  .
.
Прямым (декартовым) произведением двух множеств А и В называется множество  , состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
Прямое произведение n множеств  (обозначается
(обозначается  ) называется множеством всех векторов
) называется множеством всех векторов  , длины n таких, что
, длины n таких, что  ,
,  , ...,
, ...,  .
.
Замечание:
 .
.
Прямым (декартовым) произведением двух множеств А и В называется множество  , состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
Теорема (о мощности прямого произведения множеств).
Пусть  - конечные множества и
- конечные множества и 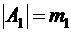 ,
,  , ... ,
, ... ,  . Тогда мощность множества
. Тогда мощность множества  равна произведению мощностей множеств
равна произведению мощностей множеств  :
:
 .
.
Следствие: 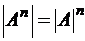 .
.
Пример: Заданы три множества: А = {0, 1, 2}, B = {4, 6, 8, 10} и С = {g}. Определить множества  ,
,  ,
,  ,
,  ,
, 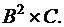
Решение:
При получении множества  надо перечислить все пары, составленные их элементов этих множеств. Применяем лексико-графическое упорядочение. По теореме о мощности прямого произведения множеств можно сказать, что искомых пар будет
надо перечислить все пары, составленные их элементов этих множеств. Применяем лексико-графическое упорядочение. По теореме о мощности прямого произведения множеств можно сказать, что искомых пар будет 
При составлении первой пары в качестве первой координаты берем 1-ый элемент множества А, в качестве второй координаты – 1-ый элемент множества В. Получаем пару (0, 4).
При составлении следующей пары в качестве первой координаты оставляем 1-ый элемент множества А, в качестве второй координаты – 2-ой элемент множества В. Получаем пару (0, 6).
Затем, получаем пары (0, 8), (0, 10). Заметим, здесь первая координата фиксирована, а вторая пробегает весь список возможных элементов множества В.
После этого заменяем первую координату на 1, а вторая координата снова пробегает весь список возможных элементов множества В.
Получаем пары (1, 4), (1, 6), (1, 8), (1, 10). И так далее.
Таким образом,
 Для получения
Для получения  можно поменять метами первые и вторые координаты в каждой паре предыдущего множества. Из чего, в частности, следует, что
можно поменять метами первые и вторые координаты в каждой паре предыдущего множества. Из чего, в частности, следует, что  Но лучше использовать лексико-графический порядок. Элементов этого множества тоже 12. Тогда
Но лучше использовать лексико-графический порядок. Элементов этого множества тоже 12. Тогда
 Множество
Множество  строится из соображений, что в качестве первой координаты берут элементы «первого» множества А, а в качестве второй – элементы «второго» множества А. Понятно, что в этом случае, часть пар будет заведомо с одинаковыми координатами. Заметим, что
строится из соображений, что в качестве первой координаты берут элементы «первого» множества А, а в качестве второй – элементы «второго» множества А. Понятно, что в этом случае, часть пар будет заведомо с одинаковыми координатами. Заметим, что 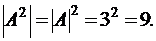
 .
.
При построении множества  надо помнить, что его элементами являются уже не пары, а тройки (вектора длины 3). Значит, для перечисления элементов
надо помнить, что его элементами являются уже не пары, а тройки (вектора длины 3). Значит, для перечисления элементов  необходимо сначала зафиксировать 1 элемент А на первом месте и 1 элемент В на втором месте, а третья координата пробегает весь список элементов третьего множества, то есть А. Получаем тройки (0, 4, 0), (0, 4, 1), (0, 4, 2).
необходимо сначала зафиксировать 1 элемент А на первом месте и 1 элемент В на втором месте, а третья координата пробегает весь список элементов третьего множества, то есть А. Получаем тройки (0, 4, 0), (0, 4, 1), (0, 4, 2).
Затем первая координата остается той же, вторая меняется на следующий по списку (второй) элемент В, а третья снова пробегает весь список элементов множества А. Получаем тройки (0, 6, 0), (0, 6, 1), (0, 6, 2).
Затем первая координата остается той же, вторая меняется на следующий по списку (третий) элемент В, а последняя снова пробегает весь список элементов множества А. Получаем тройки (0, 8, 0), (0, 8, 1), (0, 8, 2).
Последняя группа троек с первой координатой, равной 0 – (0, 10, 0), (0, 10, 1), (0, 10, 2).
Затем надо заменить первую координату на 1 и повторить перебор претендентов на второе и третье место. Затем первую координату полагаем равной 2.
Удобно заранее определить, что количество искомых троек будет найдено по теореме о мощности прямого произведения множеств: 
Тогда






 .
.
Мощность множества  равна
равна  . А именно, 4 с первой координатой 4, 4 с первой координатой 6, 4 с первой координатой 8 и 4 с первой координатой 10.
. А именно, 4 с первой координатой 4, 4 с первой координатой 6, 4 с первой координатой 8 и 4 с первой координатой 10.




 .
.
Проекцией вектора  длины n на i-ю ось называется его i-я координата (обозначение
длины n на i-ю ось называется его i-я координата (обозначение  ).
).
Проекцией вектора  на оси с номерами
на оси с номерами 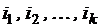 называется вектор
называется вектор  длины k (обозначение
длины k (обозначение  ).
).
Пусть V – множество векторов одинаковой длины.
Проекцией множества векторов V на i-ось называется множество проекций всех векторов из V на i-ось:
 .
.
Проекция множества векторов V на оси с номерами 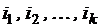 :
:
 .
.
Полезно помнить следующее:
- проекция вектора на одну ось – это вектор из одной координаты (скаляр),
- проекция вектора на две оси – вектор из двух координат,
- проекция вектора на три оси – вектор из трех координат, и так далее;
- проекция множества векторов на одну ось – это множество векторов из одной координаты (множество скаляров),
- проекция множества векторов на две оси – множество векторов из двух координат,
- проекция множества векторов на три оси – множество векторов из трех координат, и так далее.
Примеры:
1) Проекция точки плоскости на 1-ю ось – ее абсцисса, на 2-ю ось – ее ордината.
2) Дано множество векторов
 .
.
Тогда
 – это вектор из одной координаты вектора
– это вектор из одной координаты вектора 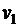 , а именно, первой координаты;
, а именно, первой координаты;
 – это вектор из одной координаты вектора
– это вектор из одной координаты вектора  , а именно, третьей;
, а именно, третьей;
 – это вектор из одной координаты вектора
– это вектор из одной координаты вектора  , а именно, второй;
, а именно, второй;
 – это вектор из двух координат вектора
– это вектор из двух координат вектора  , а именно первой и второй;
, а именно первой и второй;
 – это вектор из двух координат вектора
– это вектор из двух координат вектора  , а именно второй и третьей;
, а именно второй и третьей;
 – это вектор из двух координат вектора
– это вектор из двух координат вектора 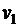 , а именно первой и третьей;
, а именно первой и третьей;
 – это множество векторов, составленных из первых координат элементов V. Они все различны, поэтому
– это множество векторов, составленных из первых координат элементов V. Они все различны, поэтому  ;
;
 – это множество векторов, составленных из вторых координат элементов V. Они все одинаковы, поэтому
– это множество векторов, составленных из вторых координат элементов V. Они все одинаковы, поэтому  ;
;
 – это множество векторов, составленных из третьих координат элементов V. Две из трех одинаковы, поэтому
– это множество векторов, составленных из третьих координат элементов V. Две из трех одинаковы, поэтому  ;
;
 – это множество векторов, составленных из первых и вторых координат векторов множества V. Все проекции различны, поэтому
– это множество векторов, составленных из первых и вторых координат векторов множества V. Все проекции различны, поэтому  ;
;
 – это множество векторов, составленных из вторых и третьих координат векторов множества V. Две их трех проекций одинаковы, поэтому
– это множество векторов, составленных из вторых и третьих координат векторов множества V. Две их трех проекций одинаковы, поэтому  ;
;
 – это множество векторов, составленных из первых и вторых координат векторов множества V. Все проекции различны, поэтому
– это множество векторов, составленных из первых и вторых координат векторов множества V. Все проекции различны, поэтому  .
.
3)  . Чему равна
. Чему равна  ? Ее найти нельзя, так как заданное множество V – множество векторов разной длины, в отношении которых никаких определений не было сделано.
? Ее найти нельзя, так как заданное множество V – множество векторов разной длины, в отношении которых никаких определений не было сделано.
Тема 3. Комбинаторика
Одно из основных правил комбинаторики – правило суммы. Его классическая формулировка имеет вид: если элемент  можно выбрать k способами, а элемент
можно выбрать k способами, а элемент  можно выбрать m способами, тогда
можно выбрать m способами, тогда  или
или  можно выбрать k + m способами. Например, если в вазе 5 яблок и 6 груш, то 1 фрукт (яблоко или грушу) можно выбрать 5 + 6 = 11 способами.
можно выбрать k + m способами. Например, если в вазе 5 яблок и 6 груш, то 1 фрукт (яблоко или грушу) можно выбрать 5 + 6 = 11 способами.
Современная формулировка правила суммы известна как теорема о мощности объединения множеств: количество элементов объединения двух множеств равно сумме количества элементов в первом множестве и количества элементов во втором множестве, за вычетом количества элементов их пересечения:
 . (3.1)
. (3.1)
Причем, если множества не пересекаются, то теорема приобретает вид, аналогичный классической формулировке:
 . (3.2)
. (3.2)
Для трех множеств теорема имеет следующий вид:
 (3.3)
(3.3)
Пример: Из 35 учащихся класс по итогам года имели «5» по математике – 14 человек; по физике – 15 человек; по химии – 18 человек; по математике и физике – 7 человек; по математике и химии – 9 человек; по физике и химии – 6 человек; по всем трем предметам – 4 человек.
1) Сколько человек имеют «5» по указанным предметам?
2) Сколько человек не имеет «5» по указанным предметам?
3) Имеет «5» только по математике?
4) Имеет «5» только по двум предметам?
Решение:
Введем обозначения. Обозначим буквой U множество всех учеников класса, буквой М множество учеников, имеющих «5» по математике, буквой Ф – имеющих «5» по физике, Х – имеющих «5» по химии. Тогда, согласно условию,


1) На рисунке 3.1 приведено множество, состоящее из учеников, имеющих «5» хотя бы по одному из указанных предметов.

Рис. 3.1. Множество учеников,
имеющих «5» хотя бы по одному предмету
Очевидно, что это объединение множеств М, Ф и Х. Для нахождения количества элементов объединения воспользуемся формулой (3.3).


2) На рисунке 3.2 приведено множество, состоящее из учеников, не имеющих «5» ни по одному из указанных предметов. Обозначим его буквой Н.

Рис. 3.2. Множество учеников, не имеющих «5»
по указанным предметам
Очевидно, что это разность между универсальным множеством U и объединением множеств М, Ф и Х. Для нахождения количества элементов объединения воспользуемся формулой (3.2).



3) На рисунке 3.3 приведено множество, состоящее из учеников, имеющих «5» только по математике. Обозначим его буквами ТМ.

Рис. 3.3. Множество учеников, имеющих «5»
только по математике
Очевидно, что это разность между множеством М и множествами ТМФ – имеющих «5» только по математике и физике, ТМХ – имеющих «5» только по математике и химии, и  .
.
Тогда
 (3.4)
(3.4)
 (3.5)
(3.5)



4) На рисунке 3.4 приведено множество, состоящее из учеников, имеющих «5» только по двум предметам. Обозначим его Т2. Очевидно, что Т2 является суммой трех непересекающихся множеств ТМФ, ТМХ, ТФХ. Используя (3.4), (3.5) и то, что

получим:


Рис. 3.4. Множество учеников, имеющих «5»
только по двум предметам
Тогда 
Другое основное правило комбинаторики – правило произведения. Его классическая формулировка имеет вид: если элемент  можно выбрать k способами, а элемент
можно выбрать k способами, а элемент  можно выбрать m способами, тогда
можно выбрать m способами, тогда  и
и  можно выбрать km способами. Например, если на гору ведут 2 дороги, а с горы – 3 дороги, то путь через перевал (дорогу на гору и дорогу с горы) можно выбрать
можно выбрать km способами. Например, если на гору ведут 2 дороги, а с горы – 3 дороги, то путь через перевал (дорогу на гору и дорогу с горы) можно выбрать  способами.
способами.
Современная формулировка правила произведения известна как теорема о мощности прямого произведения множеств: количество элементов произведения двух множеств равно произведению количества элементов в первом и во втором множестве:
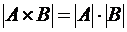 . (3.6)
. (3.6)
Правило произведения можно применять для любого количества конечных множеств.
Пример: 1) Сколько четырехзначных чисел можно составить из цифр множества  ? 2) в скольких из них только одна «3»?
? 2) в скольких из них только одна «3»?
Решение:
1) Четырехзначное число – это вектор длины 4, первая координата которого не может равняться «0».
Значит, все четырехзначные числа составляют множество  Здесь
Здесь 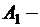 цифры, претендующие на первое место числа,
цифры, претендующие на первое место числа,  цифры, претендующие на второе место, и так далее.
цифры, претендующие на второе место, и так далее.
Так как на первом месте не может стоять «0» значит, на него претендуют цифры «1», «2», «3», «4». То есть 
На втором месте может стоять любая цифра из «0», «1», «2», «3», «4». То есть  Аналогично, на третьем и четвертом местах могут стоять любые цифры, значит
Аналогично, на третьем и четвертом местах могут стоять любые цифры, значит 
Тогда по правилу произведения:

2) Пусть искомое множество чисел – В.
Пусть  подмножество его элементов, где «3» стоит на первом месте. Здесь
подмножество его элементов, где «3» стоит на первом месте. Здесь  цифры, претендующие на первое место, а именно «3» («тройка»). Таким образом,
цифры, претендующие на первое место, а именно «3» («тройка»). Таким образом,  На каждом из оставшихся мест не может быть «3», значит список претендентов: «0», «1», «2», «4». Откуда,
На каждом из оставшихся мест не может быть «3», значит список претендентов: «0», «1», «2», «4». Откуда,  Значит, таких чисел будет:
Значит, таких чисел будет:

Пусть теперь «3» стоит на втором месте. Тогда претендентов на первое место – 3 («1», «2», «4»), на второе место – 1 (только «3»), на третье место – 4 («0», «1», «2», «4») и на четвертое место – те же 4 элемента. В итоге таких чисел 
Если «3» стоит на третьем месте числа, то, по аналогии, их тоже 54, если на последнем – 54. То есть 54 надо умножить на число способов выбрать место по «3» среди второго, третьего и четвертого, то есть на 3.
Таким образом, искомое количество чисел найдется по формуле:

Замечание:Факториалом натурального числаn называется функция, находимая по формуле:

Основные свойства факториала:
1) 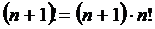 ; 2)
; 2)  .
.
Из правила произведения выводятся различные комбинаторные формулы (комбинаторные числа). Перечислим основные из них.
Число размещений без повторений из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k различными координатами.
Число размещений без повторений находится по формуле:
 (3.7)
(3.7)
Пример: Сколькими способами можно построить 3-буквенное слово из букв множества так, что бы всебуквы в слове были различны?
так, что бы всебуквы в слове были различны?
Решение:В данном случае составляется вектор (слово) из трех различных букв (k = 3), причем буквы выбираются из множества с пятью различными элементами (n = 5). Количество таких слов (3.7) равно числу размещений без повторений из 5 по 3.
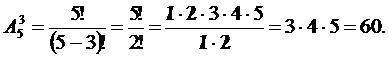
Число размещений с повторениями из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k координатами, среди которых могут быть одинаковые.
Число размещений с повторениями находится по формуле:
 . (3.8)
. (3.8)
Пример: Человек забыл последние три цифры номера телефона. Сколько вариантов номеров он может перебрать?
Решение:
Здесь будет столько номеров, сколько можно составить векторов длины 3 (k = 3) с любыми цифрами из множества с десятью цифрами  (n = 10). Тогда по формуле (3.8) получим:
(n = 10). Тогда по формуле (3.8) получим:
 .
.
Число перестановок без повторений из n элементов – это число способов, сколькими можно расположить на n различных местах n различных элементов.
Число перестановок без повторений находится по формуле:
 . (3.9)
. (3.9)
Пример: 1) Сколькими способами можно расставить на книжной полке 5 различных книг? 2) В скольких случаях две определенные книги А и В окажутся рядом?
Решение:
1) Согласно определению числа размещений без повторений, 5 книг на 5 местах можно расставить 5! различными способами. Значит общее число расстановок (перестановок) найдется по формуле (3.9):
 .
.
2) Пусть множество А составляют такие расстановки книг, где две определенные книги окажутся рядом. Для нахождения количества способов совершить такие расстановки, надо воспользоваться замечанием.
Замечание:
 , (3.10)
, (3.10)
где х – число способов выбрать нужные места; у – число способов расположить на них нужные элементы; z – число способов расположить остальные элементы на оставшихся местах.
На рисунке 3.5 приведена схема расстановки книг. В нашем случае – нужные места, это два места рядом. Выбор двух мест рядом из 5 мест производится путем перебора. На рисунке видно, что это пары мест под номерами 12, 23, 34, 45. В итоге этих пар – 4.
Таким образом, в формуле (10) х = 4.

Рис. 3.5. Схема выбора нужных мест
На рисунке 36 показано, как на двух выбранных местах можно расставить две 2 книги А и В.

Рис. 3.6. Схема расстановки нужных элементов
на выбранных местах
Вообще говоря, то, что для каждой пары выбранных мест имеется ровно два варианта расстановки книг А и В, можно было найти по формуле (3.9). Действительно, 2 элемента на 2 местах можно расставить 2! различными способами. Таким образом, в формуле (3.10) y = 2! = 2.
На рисунке 3.7 показано, как на оставшихся 3 местах можно расставить остальные три книги. При этом, положение книг А и В уже зафиксировано.

Рис. 3.7. Схема расстановки остальных элементов
на оставшихся местах
Заметим, что количество вариантов расстановки оставшихся 3 книг на оставшихся 3 местах можно было найти по формуле (3.9). Действительно, 3 элемента на 3 местах можно расставить 3! различными способами. Таким образом, в формуле (3.10) z = 3! = 6.
В итоге, искомое количество расстановок равно:
 .
.
Число перестановок с повторениями из n элементов, среди которых  одинаковых,
одинаковых,  одинаковых, …,
одинаковых, …,  одинаковых, причем
одинаковых, причем  , находится по формуле:
, находится по формуле:
 . (3.11)
. (3.11)
Решим задачу.Известно, чточетыре цифры 1, 2, 3, 4 можно переставлять друг с другом 4! различными способами. В слове «мама» – 4 буквы. Но перестановок из этих букв можно составить не 4! = 24, а всего лишь 6:
мама, маам, ммаа, амам, аамм, амма.
Чтобы понять, как это случилось, поставим в соответствие цифрам 1 и 2 букву «м», а цифрам 3 и 4 – букву «а». Тогда, например, перестановке цифр 1234 – соответствует слово «ммаа», а перестановке 1324 – слово «мама».
Но слово «ммаа» соответствует не только перестановке 1234, но и перестановки 2134, 1243, 2143. Если цифры 1 и 2 меняются местами, то в соответствующем слове меняются местами две буквы «м», следовательно, само слово остается неизменным. Таким образом, среди 24 перестановок четырех указанных букв будут одинаковыми 2! тех, которые отличаются лишь сменой мест букв «м», а также 2! тех, которые отличаются лишь переменой букв «а».
И тогда это число различных слов будет меньше 4! в 2!2! раза:
 .
.
Пример: 1) Сколькими способами можно получить слово «обороноспособность», переставляя местами карточки разрезной азбуки, с буквами О, Б, О, Р, О, Н, О, С, П, О, С, О, Б, Н, О, С, Т, Ь? 2) Сколько различных слов можно составить переставляя карточки разрезной азбуки с буквами О, Б, О, Р, О, Н, О, С, П, О, С, О, Б, Н,
О, С, Т, Ь?
Решение:
1) Чтобы ответить на 1 вопрос, воспользуемся правилом произведения. Для получения слова «обороноспособность» при перестановке местами карточек разрезной азбуки с указанными буквами, надо выяснить, сколько карточек претендует на каждое из 18 мест, с тем, чтобы в итоге получилось нужное слово. Заметим, что букв «о» в слове  , букв «б» –
, букв «б» –  , букв «р» –
, букв «р» – 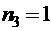 , букв «н» –
, букв «н» – 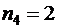 , букв «с» –
, букв «с» –  , букв «п» –
, букв «п» –  , букв «т» –
, букв «т» – 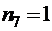 , букв «ь» –
, букв «ь» –  .
.
Так на первое место – 7 претендентов, так как первую букву слова «обороноспособность» (букву «о») можно выбрать 7 способами. На втором месте – буква «б». Их среди карточек 2 штуки. Значит, претендентов на второе место – 2. На третье место, где тоже стоит буква «о», уже только 6 претендентов, так как одна из 7 карточек с буквой «о» использована.
Таким образом, количество элементов множества А – всех перестановок 18 карточек, приводящих к слову «обороноспособность» надеется как произведение:

 .
.
2) Чтобы определить, сколько различных слов можно составить переставляя карточки разрезной азбуки с буквами О, Б, О, Р, О, Н, О, С, П, О, С, О, Б, Н, О, С, Т, Ь, нужно восполь-зоваться формулой (3.11). Здесь общее число элементов n = 18. Причем эти элементы делятся на 8 групп с одинаковыми элементами, количества которых:
 ,
,  ,
, 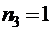 ,
, 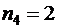 ,
,  ,
,  ,
, 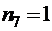 ,
,  ;
;
 .
.
Тогда по формуле (11) искомое количество различных слов будет равно:

Число сочетаний без повторений из n по k – это число способов, сколькими можно из n различных элементов выбрать k штук без учета порядка.
Формула для нахождения числа сочетаний без повторений имеет вид:
 . (3.12)
. (3.12)
Свойства:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
5)  ;
;
6)  ; 7)
; 7)  .
.
С помощью числа сочетаний без повторений чаще всего решают урновую задачу – задачу, в которой производится неупорядоченный выбор сразу нескольких элементов из заданной совокупности.
Пример: В урне 7 шаров. Из них 3 белых и 4 черных шара. Наугад выбирают 3 шара. 1) Сколькими способами это можно сделать? 2) В скольких случаях среди них будет: А) один белый; В) один черный; С) хотя бы один белый шар?
Решение:
Построим схему урновой задачи (см. рис. 3.8).

Рис.3.8. Схема урновой задачи
1) Общее число способов выбрать 3 элемента их 7 без учета порядка найдется как число сочетаний без повторений из 7 по 3по формуле (3.12).

То же самое можно было найти, воспользовавшись свойством 7.
2) Для нахождения числа способов выбрать такие три шара, чтобы среди них был 1 белый и 2 черных, надо найти отдельно число способов выбрать 1 белый шар из 3 белых и число способов выбрать 2 черных шара из 4 черных, и перемножить их согласно правилу произведения.

Здесь были использованы свойства 3 и 6.
Для нахождения числа способов выбрать такие три шара, чтобы среди них был 2 белых и 1 черный, надо найти отдельно число способов выбрать 2 белых шара из 3 белых и число способов выбрать 1 черный шара из 4 черных, и перемножить их.

Здесь были использованы свойства 4 и 3.
Для нахождения числа способов выбрать такие три шара, чтобы среди них был хотя бы 1 белый, воспользуемся подходом «от обратного». Для этого найдем количество способов, выбора таких трех шаров, где нет белых шаров, и вычтем это число из общего количества троек выбранных шаров.
Среди 3 белых шаров берем 0 белых, среди 4 черных – 3 черных.
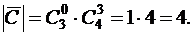
Здесь были использованы свойства 1 и 4.
Тогда искомое число равно:

Тема 4. Соответствия
Соответствием множеств А и В называется подмножество G такое, что  . Если
. Если  , то говорят, что «bсоответствует aпри соответствии G».
, то говорят, что «bсоответствует aпри соответствии G».
Область определения соответствия G – множество пр1 G Í A.
Область значений соответствия G – множество пр2G Í B.
Соответствие G называетсявсюду (полностью) определенным– если пр1 G = А (в противном случае – частично определенное соответствие).
Соответствие G называетсясюрьективным, если пр2 G = B.
Образэлемента aв множестве B при соответствии G – это множество всех элементов  , которые соответствуют
, которые соответствуют  . Обозначим образ а – G(a).
. Обозначим образ а – G(a).
Прообразэлемента b в множестве А при соответствии G – это множество всех  , которым соответствует
, которым соответствует  . Обозначим прообраз b – G -1(b).
. Обозначим прообраз b – G -1(b).
Образом множестваСÎ пр1 G называется объединение образов всех элементов С. Прообразом множестваD Î пр2 G называется объединение прообразов всех элементов D.
Соответствие G называетсяфункциональным (однозначным)соответствием, если образом любого элемента из пр1 G является единственный элемент из пр2 G. Иначе говорят, соответствие G обладает свойством единственности образа.
Соответствие G называетсяинъективнымсоответствием, если прообразом любого элемента из пр2 G является единственный элемент из пр1 G. Иначе говорят, соответствие G обладает свойством единственности прообраза.
Соответствие F является функцией типа  , если оно функционально. Обозначение функции:
, если оно функционально. Обозначение функции:  .
.
Соответствие G является отображением множества А в множество В, если оно функционально и полностью определено.
Отображение  будет отображением А в В, если G – не сюрьективно.
будет отображением А в В, если G – не сюрьективно.
Отображение  будетотображением А на В, если G – сюрьективно.
будетотображением А на В, если G – сюрьективно.
Соответствие G является взаимно однозначным, если оно: 1) всюду определено; 2) сюрьективно; 3) функционально; 4) инъективно.
Преобразованием множества Аназывается отображение типа 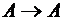 .
.
Функция типа  называется n-местной функцией (
называется n-местной функцией (  ).
).
Соответствие  называется обратным к соответствию
называется обратным к соответствию  , если Н таково, что
, если Н таково, что 
 . Можно обозначить обратное отношение
. Можно обозначить обратное отношение  .
.
Если соответствие, обратное к функции  является функциональным, то оно называется функцией, обратной к f . Обозначим обратную функцию
является функциональным, то оно называется функцией, обратной к f . Обозначим обратную функцию  .
.
Пусть дана функция  . Соответствие
. Соответствие  является функцией тогда и только тогда, когда f инъективна, и
является функцией тогда и только тогда, когда f инъективна, и  является отображением тогда и только тогда, когда f инъективна и сюрьективна (т.е. биективна).
является отображением тогда и только тогда, когда f инъективна и сюрьективна (т.е. биективна).
Утверждение: Для функции  существует обратная функция
существует обратная функция  тогда и только тогда, когда f является взаимно однозначным соответствием между своей областью определения и областью значений.
тогда и только тогда, когда f является взаимно однозначным соответствием между своей областью определения и областью значений.
Пусть даны функции  и
и  .
.
Функция  называется композицией функций f и g, если
называется композицией функций f и g, если  (обозначение
(обозначение  ). Часто говорят, что h получена подстановкой fв g.
). Часто говорят, что h получена подстановкой fв g.
Для многоместных функций  и
и  возможны различные варианты подстановки f в g, задающие функции различных типов. Например, при
возможны различные варианты подстановки f в g, задающие функции различных типов. Например, при  и
и  функция
функция  имеет 6 аргументов и тип
имеет 6 аргументов и тип  .
.
Для множества многоместных функций типа 
 возможны любые подстановки функций друг в друга, а также любые переименования аргументов. Например, переименование
возможны любые подстановки функций друг в друга, а также любые переименования аргументов. Например, переименование  в
в  из функции
из функции  четырёх аргументов порождает функцию трёх аргументов:
четырёх аргументов порождает функцию трёх аргументов:  .
.
Функция, полученная из функций  некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией функций
некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией функций  . Выражение, задающее эту суперпозицию и содержащее функциональные знаки, скобки и символы аргументов, называется формулой.
. Выражение, задающее эту суперпозицию и содержащее функциональные знаки, скобки и символы аргументов, называется формулой.
Пример 4.1.
Соответствие G =  является подмножеством прямого произведения множеств
является подмножеством прямого произведения множеств  и
и  .
.
Определить свойства соответствия.
Является ли оно функцией? Отображением? Почему?
Является ли оно взаимно однозначным?
Решение.
На рисунке 4.1 приведена схема соответствия G.
Множества А и В обозначены кругами Эйлера. Внутри каждого множества указаны все его элементы. Если элемент А связан с элементом В соответствием G, то на рисунке эти элементы связаны стрелкой.
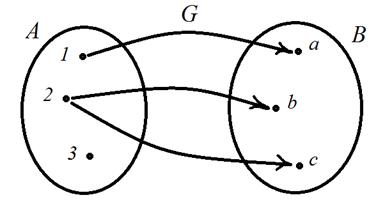
Рис. 4.1 Соответствие 
Найдем область определения соответствия G – множество пр1 G Í A. Так как соответствие – это совокупность векторов длины 2, то его проекция на 1 ось – это множество всех первых координат этих векторов.
В нашем случае, пр1 G Í = {1, 2}. Здесь всего два элемента, так как во 2-ой и 3-ей паре множества G одинаковые первые координаты. Откуда можно сделать вывод, что  . Согласно определению, это означает, что соответствие G является частично определенным. Действительно, так как пары с первой координатой 3 в соответствии G нет, значит G определено не на всех элементах множества А, то есть оно определено не полностью (частично).
. Согласно определению, это означает, что соответствие G является частично определенным. Действительно, так как пары с первой координатой 3 в соответствии G нет, значит G определено не на всех элементах множества А, то есть оно определено не полностью (частично).
Найдем область значений соответствия G – множество пр2 G Í В. Это множество всех вторых координат этих пар, входящих в соответствие G .
В нашем случае, пр2 G = {a, b, c}. Откуда можно сделать вывод, что  . Согласно определению, это означает, что соответствие G является сюрьективным.
. Согласно определению, это означает, что соответствие G является сюрьективным.
Найдем образ каждого элемента области определения.
G(1) = {a}, так как в множестве G имеется единственная пара с первой координатой 1. Это пара (1, а). То есть элементу 1 из области определения соответствует единственный элемент а из области значений. На рисунке 4.1 видно, что из 1 идет единственная стрелка в элемент а.
G(2) = {b, c}, так как в множестве G имеется две пары с первой координатой 2. Это пары (2, b) и (2, c). То есть элементу 2 из области определения соответствует два элемента b и c из области значений. На рисунке 4.1 видно, что из 2 идет две стрелки в b и в c.
Образ элемента 3 не ищем, так как он не принадлежит области определения.
Отсюда можно сделать вывод: так как единственности образа нет, то соответствие G не является функциональным.
Найдем прообраз каждого элемента области значений.
G -1(а) = {1}, так как в множестве G имеется единственная пара со второй координатой а. Это пара (1, а). То есть элемент а из области значений соответствует единственному элементу 1из области определений. На рисунке 4.1 видно, что в а идет единственная стрелка из элемента 1.
G -1(b) = {2}, так как в множестве G имеется единственная пара со второй координатой b. Это пара (2, b). То есть элемент b из области значений соответствует единственному элементу 2из области определений. На рисунке 4.1 видно, что в b идет единственная стрелка из элемента 2.
G -1(c) = {2}, так как в множестве G имеется единственная пара со второй координатой c. Это пара (2, c). То есть элемент c из области значений соответствует единственному элементу 2из области определений. На рисунке 4.1 видно, что в c идет единственная стрелка из элемента 2.
Отсюда можно сделать вывод: так как единственности прообраза есть, то соответствие G является инъективным.
Таким образом, соответствие G обладает свойствами:
1) не полностью (частично) определено,
2) сюрьективно,
3) не функционально,
4) инъективно.
Ответим на следующие далее вопросы.
Соответствие G не является функцией, так как оно не функционально.
Соответствие G не является отображением, так как оно не функционально и не полностью определено.
Соответствие G не является взаимно однозначным, так как оно сюрьективно и инъективно, но не функционально и не полностью определено.
Пример 4.2.
Соответствие H =  является подмножеством прямого произведения множеств
является подмножеством прямого произведения множеств  и
и  .
.
Определить свойства соответствия.
Является ли оно функцией? Отображением? Почему?
Является ли оно взаимно однозначным?
Решение.
На рисунке 4.2 приведена схема соответствия G.

Рис. 4.2 Соответствие 
Найдем область определения соответствия H – множество пр1 H Í M. Так как соответствие – это совокупность векторов длины 2, то его проекция на 1 ось – это множество всех первых координат этих векторов.
В нашем случае, пр1 H = {k, p, q}. Откуда можно сделать вывод, что  . Согласно определению, это означает, что соответствие H является полностью определенным.
. Согласно определению, это означает, что соответствие H является полностью определенным.
Найдем область значений соответствия H – множество пр2 H Í N. Это множество всех вторых координат этих пар, входящих в соответствие H .
В нашем случае, пр2 H = {2, 4}. Здесь всего два элемента, так как во 1-ой и 3-ей паре множества H одинаковые вторые координаты. Откуда можно сделать вывод, что  . Согласно определению, это означает, что соответствие H является несюрьективным.
. Согласно определению, это означает, что соответствие H является несюрьективным.
Найдем образ каждого элемента области определения.
H(k) = {2}, так как в множестве H имеется единственная пара с первой координатой k. Это пара (k, 2). То есть элементу k из области определения соответствует единственный элемент 2из области значений. На рисунке 4.2 видно, что из k идет единственная стрелка в элемент 2.
H(p) = {4}, так как в множестве H имеется единственная пара с первой координатой p. Это пара (p, 4). То есть элементу p из области определения соответствует единственный элемент 4из области значений. На рисунке 4.2 видно, что из p идет единственная стрелка в элемент 4.
H(q) = {2}, так как в множестве H имеется единственная пара с первой координатой q. Это пара (q, 2). То есть элементу q из области определения соответствует единственный элемент 2из области значений. На рисунке 4.2 видно, что из q идет единственная стрелка в элемент 2.
Отсюда можно сделать вывод: так как есть единственность образа, то соответствие H является функциональным.
Найдем прообраз каждого элемента области значений.
H -1(2) = {k, q}, так как в множестве H имеется две пары со второй координатой 2. Это пары (k, 2) и (q, 2). То есть элемент 2 из области значений соответствует двум различным элементам из области определений. На рисунке 4.2 видно, что в 2 идет две стрелки из элементов k и q.
H -1(4) = {p}, так как в множестве H имеется единственная пара со второй координатой 4. Это пара (p, 4). То есть элемент 4 из области значений соответствует единственному элементу p из области определений. На рисунке 4.2 видно, что в 4 идет единственная стрелка из элемента p.
Прообраз элемента 6 из множества N не ищем, так как он не принадлежит области значений.
Отсюда можно сделать вывод: так как единственности прообраза есть, то соответствие H не является инъективным.
Таким образом, соответствие H обладает свойствами:
5) полностью определено,
6) несюрьективно,
7) функционально,
8) неинъективно.
Ответим на следующие далее вопросы.
Соответствие H является функцией, так как оно функционально.
Соответствие H является отображением, так как оно функционально и полностью определено.
Соответствие H является отображением M в N, так как оно несюрьективно.
Соответствие H не является взаимно однозначным, так как оно полностью определено и функционально, но несюрьективно и неинъективно,
Тема 5. Отношения
Подмножество  называется n - местным отношением на множестве М. Говорят, что
называется n - местным отношением на множестве М. Говорят, что  находится в отношении R, если
находится в отношении R, если  .
.
Одноместное отношение – это просто подмножество М. Такие отношения называют признаками: элемент а – обладает признаком R, если  и
и 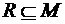 .
.
Свойства одноместных отношений это свойства подмножеств М, поэтому для случая n = 1 термин “отношение” употребляется редко.
Примером трехместного (тернарного) отношения является множество троек нападающих в хоккейной команде. Любой из нападающих находится в этом отношении со всеми теми игроками, с которыми он играет в одной тройке (один нападающий может, вообще говоря, участвовать более, чем в одной тройке).
При n = 2 – отношения называются двуместными или “бинарными”. Если a, b находятся в отношении R, это записывается aRb.
Дата добавления: 2018-04-15; просмотров: 846; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
