Определение предельной несущей способности ж.б. стены при действии N и М из плоскости стены

⇐ ПредыдущаяСтр 21 из 26Следующая ⇒

При e_oh > e_a предельную несущую способность из плоскости средних прямоугольных сечений железобетонных стен (N_с_r) рекомендуется определять посредством решения системы уравнений равновесия моментов и сил в стадии III напряженно деформированного состояния методом последовательных приближений в форме:

а) при

(6.63)

б) при

(6.64)

Уравнение относительно x_i для случая, когда и класс бетона меньше В30, получено из совместного решения зависимости (6.65) и уравнения (6.66).

(6.65)

(6.66)

В формулах (6.63) и (6.64):

N_i – несущая способность стены i-того приближения.

В первом приближении рекомендуется принимать:

(6.67)

(6.68)

N_cr – условная критическая сила.

Для железобетонных элементов прямоугольного сечения:

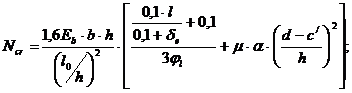(6.69)

где φ_l и δ_е – коэффициенты, определяемые по формулам (6.56 и 6.57);

коэффициент приведения.

граничное значение относительной высоты сжатой зоны бетона

(6.70)

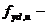предельное напряжение в арматуре сжатой зоны, принимаемое при равным 400МПа, при 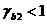500МПа (таблица 15 СниПа);

ω – характеристика сжатой зоны бетона:

(6.71)

α₂– коэффициент, принимаемый для тяжелого бетона равным 0,85, легкого бетона на пористых заполнителях – 0,8.

В случае, если высота сжатой зоны бетона при , что может иметь место в верхних этажах торцовых стен при больших значениях М и малых величинах пригруза, необходимо определять минимальную продольную силу (N_min), которая должна действовать в сечении при заданном армировании. Она вычисляется методом последовательных приближений в форме:

(6.72)

где определяется по формуле (6.59).

В качестве первого приближения:

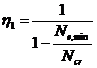здесь N_e_,_min → по формуле (6.61).

6.5.11 Определение продольной силы N в железобетонном сечении стены, соответствующей допустимой ширине раскрытия трещин при заданном сечении M_x

При наличии силовых трещин в железобетонной стене, т.е. при N>N_cr_с требуется производить расчет их раскрытия (а_cr_с) и проверку условия:

(6.73)

Допускаемая ширина продолжительного раскрытия трещин (а_cr_с,2) в ж.б. стенах, армированных сталью классов A-I, A-II, A-III, Вр-I составляет 0,3мм, а непродолжительного – а_cr_с,1=0,4мм (см. таблица 1. СниП 2.03.01-84*).

Ширина раскрытия трещин, нормальных к предельной оси внецентренно сжатого элемента, а_cr_с определяется по формуле:

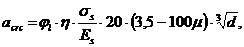(6.74)

где все обозначение в соответствии СниП 2.03.01-84*.

Напряжение в растянутой арматуре (σ_s) сжато-изогнутых обычно армированных элементов определяется по формуле:

(6.75)

где е_s – расстояние от точки приложения продольной силы N до центра тяжести площади сечения арматуры A_s;

z – расстояние от ц.т. площади сечения арматуры до точки приложения равнодействующей усилий в сжатой зоне сечения под трещиной, определяемое согласно указаниям п.4.28. СниП 2.03.01-84.

Приближенно . Подставляя эти значения z и e_s в формулу (6.75) и решая уравнение (6.74) относительно N при , получим формулу (6.76) для определения величины продольной силы N в железобетонном сечении стены при допустимой ширине раскрытия трещин и заданном М:

(6.76)

Величину следует сравнивать с расчетной нагрузкой, действующей в ј-том сечении стены ( 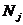) и определяемое с коэффициентом перегрузки, равным 1. В том случае, если в ј-том сечении условие (6.73) выполняется.

6.5.12 Определение предельной несущей способности среднего сечения стены при совместном действии усилий N, M_x и M_y.

Расчет средних горизонтальных сечений монолитных стен выполняется путем подбора сечений, классов бетона и армирования при действии продольной силы N и момента М_х из плоскости стены. Затем подобранное сечение при необходимости проверяется на совместное действие указанных усилий N; M_x (M_ст) и момента M_у(M_b) действующего в плоскости стены.

При эксцентриситетах приложения продольной силы в плоскости стены 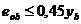(где y_b – расстояние по ширине стены от центра сечения до более сжатой грани) предельная несущая способность среднего сечения бетонной или железобетонной стены на совместное действие изгиба из плоскости и в плоскости стены определяется из условия обеспечения прочности сопротивлением только сжатой зоны сечения. Прочность сжатой зоны считается обеспеченной, если выполняется следующее условие:

, (6.77)

где N – продольная сжимающая сила в расчетном сечении стены

N_ст – предельная несущая способность среднего сечения бетонной или ж.б. стены из плоскости (см. п.п. 6.5.7…6.5.10);

N_b – предельная несущая способность среднего сечения бетонной или железобетонной стены при действии момента в плоскости (M_b).

Для продольных сечений:

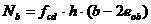, (6.78)

где h и b – толщина и ширина стены;

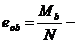эксцентриситет продольной силы в плоскости стены.

Для тавровых сечений несущих стен:

, (6.79)

где A_c – площадь сжатой зоны сечения (п.4.7. СниП 11-2281 «Каменные и армокаменные конструкции»).

При этом ширина полок в сжатой зоне сечения должна приниматься не более 3Н₀ при закреплении полки простенка перпендикулярно по направлению по четырем сторонам и 1,5Н₀ при закреплении полки по трем сторонам.

N_ц – предельная несущая способность бетонной или ж.б. стены при условном центральном сжатии без учета продольного изгиба, определяемая по формуле:

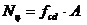, (6.80)

где А – площадь среднего сечения стены.

При эксцентриситетах приложения продольной силы в плоскости стены 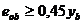несущая способность сечения обеспечивается сопротивлением сжатой и растянутой зон. Для определения размеров сжатой зоны и требуемой площади растянутой арматуры используются два уравнения равновесия: первое – равенство нулю суммы проекций всех сил на продольную ось, второе – равенство нулю суммы моментов внутренних и внешних сил, вызывающих изгиб стены в ее плоскости.

Предельное сопротивление стены сжатию при наличии сдвигающих сил в плоскости стены определяется по формуле:

, (6.81)

где τ – среднее напряжение среза в сжатой зоне

, (6.82)

A_cut – площадь сдвига, равная площади части сжатой зоны, которая расположена в пределах длины стены (без площади принимающих простенков направления).

Среднее напряжение сжатию в сжатой зоне сечения τ принимается равным предельному сопротивлению сжатию при наличии срезывающих сил в плоскости стены R_σ. Требуемая площадь сквозной продольной арматуры у растянутой грани сечения при , определяется по формуле:

, (6.83)

где А_с – площадь сжатой зоны;

σ_s – напряжения в сквозной вертикальной арматуре стены, принимаемые в зависимости от относительной высоты сжатой зоны (где размер сжатой зоны – расчетная высота сечения).

При ; при и бетоне класса В30 и выше σ_s следует определять по формуле (6.65).

Дата добавления: 2018-04-15; просмотров: 783; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 16 17 18 19 202122 23 24 25 Следующая ⇒

Мы поможем в написании ваших работ!