Побудова векторних діаграм для кола з послідовно з’єднаними елементами
Векторні діаграми для діючих значень величин будуємо згідно з другим законом Кірхгофа, записаним у векторній формі: вектор напруги, прикладеної до кола, дорівнює геометричній сумі векторів напруг на окремих її ділянках
,
де 
- напруга прикладена до кола.
Векторні діаграми будуємо для трьох випадків:
а) XL > XC ; б) XL < XC ; в) XL = XC. Причому будемо вважати, що початкова фаза струму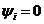 
.
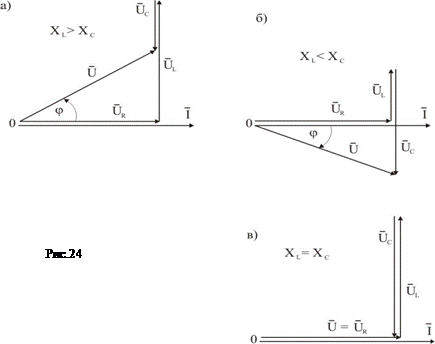
а) Розглянемо перший випадок: XL > XC; звідси за величиною UL > UC .
Векторна діаграма для цього випадку наведена на рис.24,а.
 |
На ній вздовж дійсної осі в обраному масштабі відкладений вектор струму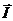 
. Потім паралельно до 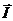відкладаємо у масштабі вектор напруги на резисторі 
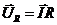. Так як на котушці індуктивності напруга випереджає струм за фазою на 900, то вектор 
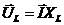повертаємо відносно вектора 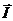на 900 проти годинникової стрілки і прикладаємо його до кінця вектора 
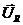. Вектор 
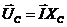- вектор напруги на конденсаторі, який відстає від вектора струму на кут 900, тому обертаємо його за годинниковою стрілкою на 900 і прикладаємо до кінця попереднього вектора, 
.
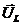Кут зсуву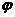 
між векторами 
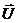та 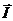при XL > XC є додатним і коло має індуктивний характер.
б) Випадок XL < XC; звідси за величиною UL < UC .
Векторна діаграма приведена на рис.24,б. При XL < XC зсув фаз між векторами 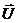та 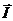є від’ємним і коло має ємнісний характер.
в) При XL = XC маємо особливий режим (рис.24,в): так як вектори 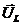і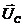 
рівні за величиною, але протилежно направлені (тобто знаходяться в протифазі), тому їх геометрична сума дорівнює нулю. Такий режим називається резонансом напруг.
|
|
|
Як видно з векторної діаграми, при резонансі напруг напруга на вході кола 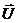чисельно дорівнює падінню напруги на активному опорі R, а зсув фаз між векторами 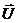та 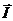дорівнює нулю. Якщо активний опір R малий, то виникає значний струм (рис. 25) та великі напруги на ємності та індуктивності, що можуть бути значно більшими, ніж напруга мережі.
Частоту змінного струму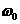 
, при якій виникає резонанс, називають резонансною. Її визначають з умови рівності реактивних опорів:
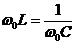, звідки 
Відношення напруги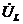 
і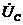 
до напруги 
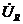називається добротністю і позначається літерою Q:
.
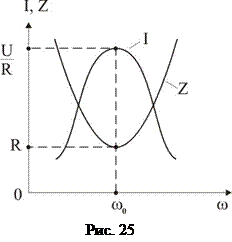
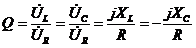Добротність визначає, у скільки разів напруга на реактивних елементах перевищує напругу на резистивному елементі.
Оскільки резонансна частота дорівнює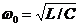 
, то добротність 
, де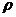 
- хвильовий опір. Хвильовим опором називають величину реактивного опору при резонансній частоті: 
.
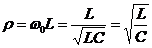Явище резонансу широко використовують в радіотехніці, телебаченні, автоматиці та інших технічних галузях. Але у промисловості резонансні явища пов’язані зі значними підвищеннями напруги на індуктивних та ємнісних елементах, що може привести до пробою їх ізоляції.
|
|
|
Трикутник напруг і опорів
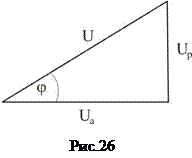а) Трикутник напруг
Аналіз векторних діаграм (рис. 24) показує, що вектор прикладеної до кола напруги можна розглядати як геометричну суму векторів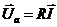 
і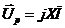 
. Вектор 
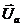(вектор результуючої напруги на активних елементах кола) співпадає за фазою з вектором струму 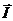, а вектор 
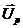(вектор результуючої напруги на реактивних елементах кола) перпендикулярний вектору 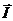і повернутий вліво від нього, якщо φ > 0 - тобто коло має індуктивний характер, або вправо від нього, якщо 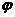< 0 (тобто коло має ємнісний характер).
В одержаному трикутнику напруг 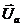(рис.26) співпадає за фазою зі струмом і називається активною складовою напруги: 
.
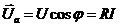Напруга 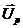зсунута за фазою на кут 
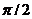відносно струму і називається реактивною складовою напруги: 
.
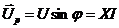Виходячи с трикутника (рис.26) напруга на
затискачах кола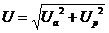 
.
б) Трикутник опорів одержуємо з трикутника
напруг.
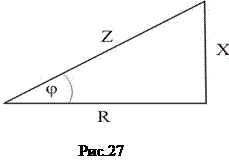
Довжини сторін трикутника опорів визначаються шляхом ділення відповідних напруг на значення струму (рис.27).
З трикутника опорів знаходимо співвідношення:
|
|
|
; 
; 
,
.
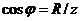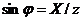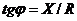Дата добавления: 2018-04-15; просмотров: 242; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!