Застосування законів Кірхгофа для аналізу складних електричних кіл
План
1. Алгоритми складання рівнянь за першим і другим законом Кірхгофа, приклади розв’язку задач.
2. Еквівалентні перетворення «трикутника» і «зірки».
3. Потенційна діаграма.
Розрахунок електричних кіл постійного струму класичним методом
Використовуючи закони Кірхгофа і Ома, можна розрахувати практично будь-яке коло. Як правило, бувають задані; схема з'єднання, а також чисельні значення і напрямки джерел ЕРС, чисельні значення опорів резисторів. Необхідно розрахуватиструми всіх гілок, а по струмах легко розраховуються потужність, падіння напруги та ін.
Отже, розв'язуючи задачу за законами Кірхгофа, спочатку потрібно визначити кількість рівнянь, які необхідно записати за 1-м та за 2-м законах Кірхгофа.
Якщо схема містить вузлів "n", а гілок "m", то слід мати за обома законами Кірхгофа "m" незалежних рівнянь, тобто таких, які не повторюються.
За 1-м закон Кірхгофа необхідно скласти рівнянь на одне менше, ніж кількість вузлів:
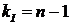
За 2-м законом Кірхгофа потрібно скласти кількість рівнянь, що визначається за формулою:
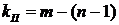
Розглянемо порядок складання рівнянь на прикладі схеми по рис.7.
2
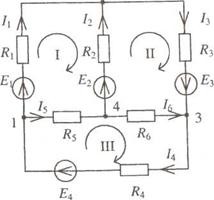
Рис.7.
За першим законом Кірхгофа:
1) Визначаємо кількість вузлів n.
У даній схемі вузлів п= 4, позначимо їх цифрами 1, 2, 3, 4. Отже, по першому закону Кірхгофа потрібно скласти три рівняння:
|
|
|
.
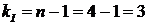2) За 1-м законом Кірхгофа не будемо складати рівняння для одного з вузлів, наприклад 4-го. Приймаємо умовно додатні напрями струмів гілок і показуємо їх на схемі. Як правило, у гілках з ЕРС ці струми направляють по ЕРС, а у пасивних гілках (що не містять ЕРС) — довільні. Бажано, щоб індекс струму гілки і опору даної гілки співпадали, тобто у гілці з R1 струм I1 і т.п.
3) Складаємо рівняння. При запису рівнянь за 1-м законом Кірхгофа будемо дотримуватися правила знаків: струми, які входять у вузол, записуємо зі знаком "плюс", а ті, які виходять із вузла — зі знаком "мінус".
Для вузла 1: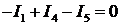 
;
Для вузла 2: 
;
Для вузла 3: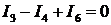 
.
За другим законом Кірхгофа:
1) Визначаємо кількість незалежних контурів. У схемі гілок т = 6, отже, кількість невідомих струмів також дорівнює т, тобто 6. За 2-м законом Кірхгофа необхідно скласти також три рівняння:
.
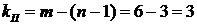2) Щоб приступити до складання рівнянь за 2-м законом Кірхгофа, необхідно вибрати контури та напрямки обходу контурів, бажано ці напрямки обирати в один бік, наприклад, за годинниковою стрілкою.
3) Складаємо рівняння. При записі рівнянь за 2-м законом Кірхгофа будемо дотримуватися правила знаків: з "плюсом" записуємо ті ЕРС, напрям яких співпадає з обраним напрямом обходу контуру (зустрічні — зі знаком "мінус"), падіння напруги на резисторі записується з плюсом, якщо співпадають напрямки струму в даній гілці і напрямок обходу контуру.
|
|
|
Виконавши ці підготовчі етапи, складаємо рівняння за 2-м законом Кірхгофа:
Контур I: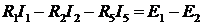 
;
Контур II: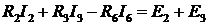 
;
Контур III: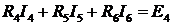 
.
Розв'язуючи сумісно ці 6 рівнянь, можна розрахувати 6 невідомих струмів. Якщо струм у якійсь гілці отримано зі знаком "мінус", це означає, що ми помилилися у напрямку струму і його необхідно направити у протилежну сторону. Проте, рішення задачі з шістьма рівняннями дуже громіздке і тому використання безпосередньо законів Кірхгофа практично доцільне для розрахунку більш простих за конфігурацією схем. А для схем, подібних наведеній на рис.1, розроблені більш прості методи розрахунку (контурних струмів, вузлових потенціалів).
Приклади розв'язку задач
Задача 1(приклад постановки прямої задачі).
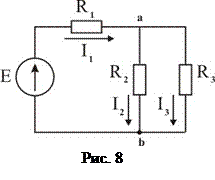
В електричному колі, наведеному на рис.8 , електрорушійна сила джерела Е=50В, а опори резисторів дорівнюють R1 =10 Ом, R2=20 Ом, R3 =20Ом. Визначити значення струмів І1, І2, І3.
Розв’язання
|
|
|
1) Для розв’язку задачі використовуємо еквівалентне перетворення:
.
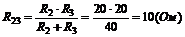2) Визначаємо еквівалентний опір схеми: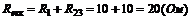 
.
3) Застосовуємо закон Ома для замкненого кола для визначення струму на нерозгалуженій ділянці кола: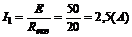 
.
4) Знаходимо напругу на ділянці аb: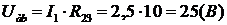 
.
5) За законом Ома визначаємо струм через резистор з опором R2: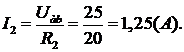 
6) За першим законом Кірхгофа знаходимо струм через резистор R3: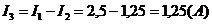 
.
7) Правильність розв’язку задачі перевіряємо за допомогою балансу потужності:
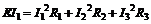
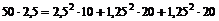
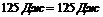
Одержуємо, що енергія джерела ЕРС дорівнює енергії, яка виділяється на резисторах. Це є доказом правильності розв’язку задачі.
Задача 2(приклад зворотної задачі). Для електричного кола (рис.8) задані значення опорів R1 =10 Ом, R2=5 Ом, R3 =10 Ом і струму І3 = 2А. Визначити струми І1 , І2 та ЕРС джерела.
Розв’язання
1) Визначаємо напругу на ділянці аb: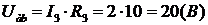 
.
2) Для розрахунку струму через резистор R2 скористаємося законом Ома для ділянки кола: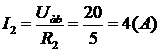 
.
3) Для знаходження струму І1 застосуємо перший закон Кірхгофа: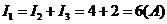 
.
4) Визначаємо падіння напруги на резисторі R1: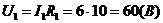 
.
5) Знаходимо ЕРС джерела за другим законом Кірхгофа: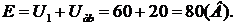 
6) Для перевірки правильності розв’язку задачі складаємо баланс потужності:
|
|
|
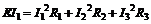
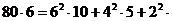10
.
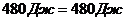Рівність лівої та правої частин рівняння балансу є доказом правильності розв’язання задачі.
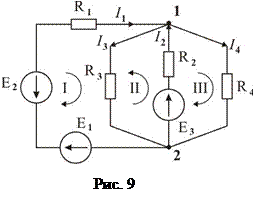Задача 3.Для електричного кола, зображеного на рис.3, з такими параметрами: E1=120B, E2=20B, E3= 80B, R1 = R2=2 Ом, R3 =40 Ом, R3 =50 Ом, визначити всі струми за допомогою методу Кірхгофа.
Розв’язання
Спочатку проводимо структурний аналіз: визначаємо кількість вузлів і незалежних контурів. Потім довільно обираємо напрямки струмів в гілках і напрямки обходу контурів (за годинниковою чи проти годинникової стрілки).
1) Кількість вузлів n=2, тому складаємо одне рівняння за першим законом Кірхгофа для вузла 2:
.
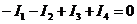2) Так як кількість незалежних контурів l=3, то складаємо три рівняння за другим законом Кірхгофа:
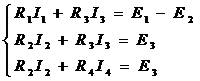
В результаті маємо систему чотирьох рівнянь, в якій кількість невідомих дорівнює кількості рівнянь.
3) Враховуючи початкові дані, розв’язуємо систему відносно струмів:
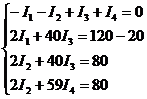
Розв’язання цієї системи рівнянь дає значення струмів:
.
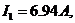
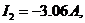
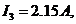
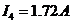Від’ємне значення струму показує, що дійсний напрямок струму протилежний.
Еквівалентні взаємні перетворення “трикутник-зірка”
Нерідко більш складні схеми вдається спростити і розрахувати Rекв, якщо застосувати перетворення "трикутник-зірка"', або "зірка-трикутник".
Необхідно пам'ятати правило, що одну схему можна заміняти на еквівалентну, якщо при тих же напругах будуть протікати ті ж самі струми або, іншими словами, якщо в заданій і еквівалентній схемах будуть рівними відносно затискачів вхідні опори.
Розглянемо перехід від трикутника з опорами R12, R23, R31 до еквівалентної зірки з опорами R1, R2, R3 (рис. 10).
Будемо вважати відомими R12, R23, R31. Виведемо формули для розрахунку R1, R2, R3. Вхідний опір на затискачах 1-2 для трикутника при розірваній гілці 3: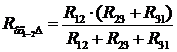 
. (1)
Вхідний опір на затискачах 1-2 для зірки:
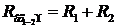. (2)
Ці вхідні опори повинні бути рівними:
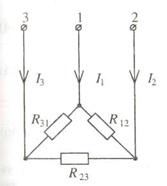
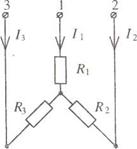
Рис.10.
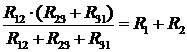. (3)
Аналогічно запишемо вхідні опори для затискачів 2-3 та 3-1:
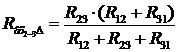. (4)
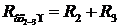. (5)
Звідси:
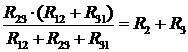. (6)
Аналогічно: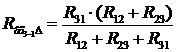 
. (7)
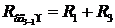. (8)
Звідси:
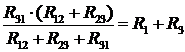. (9)
Розв'яжемо сумісно отримані рівняння (3), (6) та (9). Виконаємо для лівої та правої частин відповідно наступні алгебраїчні перетворення (3) - (6) + (9) Тоді отримаємо:
(10)
.
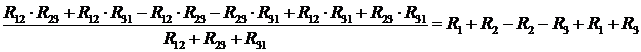Після скорочень отримаємо:
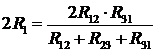. (11)
І в решті-решт:
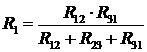. (12)
Формули для розрахунку R2та R3 можна отримати, якщо виконати аналогічні алгебраїчні перетворення:
(3)+ (6)-(9);
-(3) + (6) + (9).
Також за отриманою формулою (12) можна вивести правило визначення опору променя еквівалентної зірки: Потрібно перемножити опори тих сторін трикутника, які сходяться у вершині і поділити на суму опорів сторін трикутника.
Таким чином, формули для розрахунку R2та R3 запишемо за аналогією з (12):
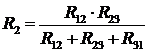. (13)
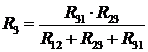. (14)
Якщо трикутник симетричний, тобто всі його сторони рівні, тоді згідно з формулами (12)-(14) опори променів еквівалентної зірки також будуть рівні:
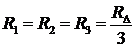. (15)
Еквівалентні взаємні перетворення “ зірка-трикутник ”
|
|
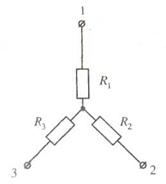
Рис. 11
Будемо вважати відомими R1, R2, R3. Виведемо формули для розрахунку R12, R23, R31.
Щоб скласти рівняння для такого перетворення, поділимо (14) на (12) відповідно, тобто ліву частину на ліву, а праву на праву, одержимо:
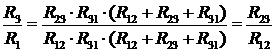. (16)
Аналогічно поділимо (14) на (13):
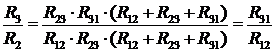. (17)
Підставимо (16) та (17) в (12):
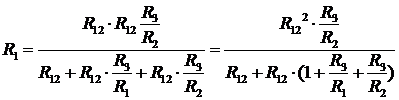. (18)
Або
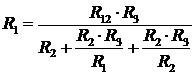. (19)
Звідси: 
. (20)
По аналогії :
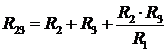. (21)
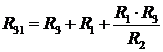. (22)
Перетворення ∆→Υ або Υ→∆ у деяких випадках дає змогу складну схему звести до змішаного з’єднання, тоді легко визначати Rекв на затискачах джерела і розраховуються всі параметри схеми.
Приклад
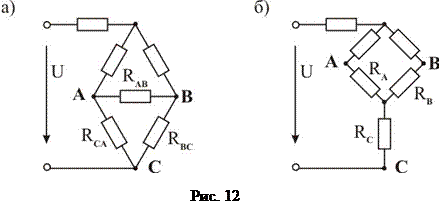
Характерним прикладом спрощення розрахунків із застосуванням метода перетворення кіл може служити перетворення мостової схеми з’єднання резистивних елементів (рис.6, а). Після заміни частини кола за схемою трикутник еквівалентним колом за схемою зірка все коло (рис.6, б) можна розглядати як змішане з’єднання резистивних елементів.
 |
Побудова потенційних діаграм
Потенційна діаграма – це графічне зображення зміни потенціалу при обході замкненого контуру. При цьому по осі абсцис відкладається опір між характерними точками, а по осі ординат – їх потенціали.
Щоб розрахувати коло методом побудови потенційної діаграми, необхідно:
а) розрахувати коло (визначити всі струми, напруги, їх напрямки, загальний опір Rзаг);
б) коло розбити характерними точками, що розділяють опори та ЕРС;
в) задати довільно напрям обходу;
г) прийняти рівним нулю потенціал однієї з точок схеми (φ=0 – з цієї точки починаємо побудову діаграми, йдучи в напрямку обходу контуру);
д) виходячи з Rзаг кола вибрати масштаб по осі абсцис і відкласти опори між характерними точками;
е) після аналізу потенціалів вузлів і ЕРС, вибрати масштаб потенціалів по осі ординат і відкласти потенціали характерних точок:
- якщо напрям обходу збігається з напрямом ЕРС, то потенціал треба відкладати із знаком “+”,
При цьому необхідно враховувати, що струм через резистор тече від більшого потенціалу до меншого, а внутрішній опір джерела ЕРС дорівнює нулю.
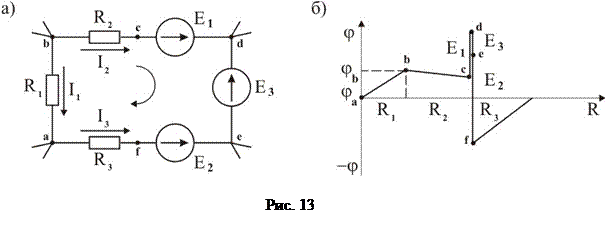
Приклад. Побудуємо векторну діаграму контуру abcd (рис. 13).
Потенціал вузла а приймаємо за нуль: φа = 0. Визначаємо потенціали інших точок за формулами: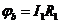 
;
;
;
;
;
.
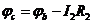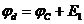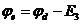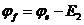У масштабі по осі абсцис відкладаємо опір кожної ділянки, пам’ятаючи, що внутрішній опір джерела ЕРС дорівнює нулю; по осі ординат у масштабі відкладаємо потенціали точок.
 |
Література:
1. Паначевний Б.І., Свергун Ю.Ф. Загальна електротехніка: Підручник.-3-є вид. – К.: Каравела, 2009 – 296с.
2. Малинівський С.М. Загальна електротехніка.- Л.:»Бескид Біт», 2003
3. Касаткин А.С., Немцов М.В. Электротехника. – М.:Энергоатомиздат, 1983
4. Титаренко М.В. Електротехніка: Навчальний посібник для студентов інженерно-технічних (неелектротехнічних) спеціальностей вузів. – К.:Кондор, 2009 – 240с.
Контрольні питання:
1. Яку мінімальну кількість рівнянь складають за першим і другим законами Кірхгофа при розрахунку електричного кола кластичним методом (методом законів Кірхгофа)?
2. Проаналізувати застосування законів Кірхгофа для розрахунку кіл постійного струму на прикладі.
3. Які бувають види еквівалентних перетворень?
4. Які умови еквівалентності перетворення?
5. Пояснити сутність перетворення трикутника опорів в зірку. Навести формулу для розрахунку опорів зірки.
6. Пояснити сутність перетворення з'єднання опорів зіркою в еквівалентний трикутник. Навести формулу для розрахунку опорів трикутника.
7. Пояснити формулу перетворення трикутника опорів в еквівалентну зірку (і зворотного перетворення).
8. Пояснити порядок побудови потенційної діаграми заданого контуру кола на прикладі.
Питання та завдання для самостійної роботи:
1. Перелічити методи розрахунку електричних кіл.
2. Пояснити сутність методу контурних струмів для розрахунку складних кіл.
3. Яку перевагу має метод контурних струмів перед класичним методом
( методом за законами Кірхгофа)? Як виводиться система рівнянь методу контурних струмів? Як у цьому методі визначаються струми гілок? Показати на прикладі.
4. У яких випадках доцільно застосовувати метод вузлових потенціалів? Як виводиться система рівнянь методу вузлових потенціалів? Як у цьому методі визначаються струми? Пояснити на прикладі.
5. За яких умов метод вузлових потенціалів має переваги перед методом контурних струмів?
6. У якому випадку при розрахунку електричних кіл застосовують метод еквівалентного генератора? Як виводиться основна формула методу еквівалентного генератора? Як визначити ЕРС еквівалентного генератора? Показати на прикладі.
Тема №2.Електричні кола однофазного синусоїдального струму
Лекція № 3
Дата добавления: 2018-04-15; просмотров: 426; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!