Електричне коло з паралельним з’єднанням елементів
При паралельному з’єднанні елементів (рис.28) рівняння за першим законом Кірхгофа для миттєвих значень та у комплексній формі мають такий вигляд:
, 
. (29)
Через провідності
- g – активну,
- bL – реактивну індуктивну,
- bC - реактивну ємнісну
струми можна записати у комплексному
вигляді:
, 
, 
,
де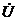 
-комплексне діюче значення напруги на вході кола; (-jbL) – комплексне значення індуктивної провідності; ( jbC ) – комплексне значення ємнісної провідності.
Тому рівняння (29) можна записати у вигляді:
. (30)
Різниця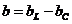 
називається реактивною провідністю, а величина 
- комплексною провідністю кола (де b > 0 при bL > bC , b < 0 при bL < bC ).
Звідси закон Ома в комплексному вигляді для розгалуженого кола:
.
Побудова векторних діаграм для кола з паралельно з’єднаними елементами
Векторні діаграми для діючих значень величин будуємо згідно з першим законом Кірхгофа, записаним у векторній формі: 
,враховуючи зсув фаз 
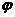між напругою і струмом і вважаючи, що початкова фаза напруги дорівнює нулю ( 
).
Векторні діаграми будуємо для трьох випадків:
а) bL > bC (рис.29,а); б) bL < bC (рис.29, б); в) bL = bC (рис.29,в).
Резонанс струмів спостерігається в розгалужених колах при умові
bL = bC. (рис.29,в). У цьому разі струми у гілках з реактивними елементами рівні і повернені в протилежні боки. Струми у гілках з реактивними елементами можуть значно перевищувати струм у нерозгалуженій ділянці кола, який в момент резонансу набуває мінімальногозначення (рис.30). Повна провідністьколадорівнює тільки активній провідності (y=g).
|
|
|
Як і при резонансі напруг, при резонансі струмів мають місце співвідношення: φ = 0 , 
.
Так як напруга на всіх елементах при паралельному з’єднанні однакова, то резонанс струмів не представляє небезпеку. Тому він широко використовується в енергетиці, радіотехніці, телебаченні, техніці зв’язку.
Трикутники струмів і провідності
а) Трикутник струмів. Аналіз векторних діаграм
(рис.29,а і б) показує, що вектор струму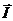 
на нерозгалуженій ділянці кола можна розглядати як векторну (геометричну) суму векторів 
і 
. В одержаному трикутнику струмів
(рис.31) вектор (вектор струму через активні елементи кола) співпадає за фазою з вектором напруги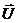 
, а вектор (вектор результуючого струму через реактивні елементи кола) перпендикулярний вектору .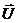
З трикутника струмів діюче значення струму 
, де 
, 
.
б) Трикутник провідностей. Розділивши кожну із сторін трикутника струмів (рис.29, а або б) на діюче значення напруги U, одержимо трикутник провідності (рис.32), подібний трикутнику струмів. Активна та реактивна провідності зображені катетами, а повна провідність – гіпотенузою прямокутного трикутника.
|
|
|
Для трикутника провідності мають місце співвідношення
, 
, 
, 
.
Розглянуті в лекції трикутники струмів та напруг є векторними, а трикутники опорів і провідностей - звичайними трикутниками.
Кут φ (зсув фаз між струмом і напругою) однаковий у трикутниках опору та провідності, тобто ці трикутники подібні. За визначенням 
, тому можна скласти співвідношення між опорами та провідностями 
та інші.
Вирази провідностей через опори та опорів через провідність мають вигляд:
Дата добавления: 2018-04-15; просмотров: 119; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!