Елементарні кола змінного струму з послідовно і паралельно з’єднаними елементами R, L. C.
План
1. Електричні кола змінного струму з послідовно з’єднаними ідеальними елементами R, L. C.
2. Векторна діаграма напруг. Співвідношення між струмом і напругою. Трикутник напруг, опорів. Резонанс напруг.
3. Електричні кола з паралельно з’єднаними елементами R, L. C. Співвідношення між струмом та напругою. Векторна діаграма струмів. Резонанс струмів. Трикутники струмів та провідностей.
4. Потужність в колі змінного струму.
Елементарні кола змінного струму з послідовно з’єднаними ідеальними елементами – резистором, конденсатором, котушкою індуктивності
Розглянемо електричне коло (рис.20), яке містить у собі послідовно з’єднані активний опір R, індуктивність L та ємність C, що живляться від ідеального джерела синусоїдального струму
. (24)
Поставимо перед собою задачу визначити напругу на кожному елементі та напругу U, яка може бути виміряною на клемах джерела струму.
Відповідно до другого закону Кірхгофа, для миттєвих значень напруг маємо:
, (25)
де 
- миттєве значення напруги на резисторі;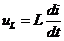 
- миттєве значення напруги на котушці індуктивності; 
- напруга на конденсаторі.
Підставивши формулу (24) в (25), одержимо:
,
де 
та 
- чисельні значення реактивних опорів котушки індуктивності і конденсатора відповідно, а величина 
називається реактивним опором схеми. Внаслідок цього маємо
|
|
|
. (26)
Використовуючи математичну формулу
, де 
,
перепишемо формулу (26) у вигляді
,
де 
- зсув фаз між напругою на вході схеми і струмом; z – чисельне значення повного опору схеми.
Напругу на затискачах джерела струму можна також знайти, використовуючи другий закон Кірхгофа у комплексному вигляді, тобто
. (27)
Враховуючи, що через кожен з елементів протікає один і той же струм, можемо записати
, 
, 
,
або , 
, 
.
Це дає можливість рівняння (27) записати у вигляді:
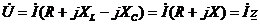. (28)
Величина 
є еквівалентним комплексним повним опором схеми, а реактивний опір ( ) є уявною частиною комплексного опору кола. Комплексний повний опір схеми, як будь-яка комплексна величина, може бути представленою у вигляді : 
, де 
- модуль опору,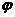 
- зсув фаз між напругою на вході кола та струмом. Реактивний опір в залежності від величини XL і ХС може носити індуктивний (XL > ХС), або ємнісний характер (XL < ХС).
|
|
|
З формули (28) маємо класичний закон Ома для нерозгалуженого кола змінного струму в комплексному вигляді: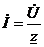 
.
Такий же вигляд буде мати закон Ома для діючих значень струму і напруги: 
.
Приклад 1.
Маємо коло з двох елементів R і С. Визначити модуль повного опору кола z.
Комплексний опір кола 
, зсув фаз між напругою на схемі і струмом 
. Комплексний опір можна показати на комплексній площині (рис. 21).
З рисунку видно, що
.
Приклад 2.
Електричне коло змінного струму складається з послідовно з’єднаних резистора та котушки індуктивності (рис.22): R = 25Ом, L=0,1Гн. Визначити діюче значення струму, якщо діюче значення напруги, прикладеної до кола, дорівнює 220В.
Розв’язання
Задачу можна розв’язувати або в комплексному вигляді, або в алгебраїчному для діючих величин. Застосуємо другий метод.
Реактивний опір котушки індуктивності: 
Ом.
Повний опір кола:
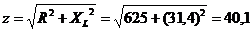Ом.
Зсув фаз між напругою на вході кола і струмом через елементи (рис.23): 
.
Діюче значення струму: 
.
Дата добавления: 2018-04-15; просмотров: 158; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!