Логические схемы и логические выражения

Удобным способом представления логических выражений являются логические схемы. Вот как изображаются на таких схемах три основные логические операции:

 

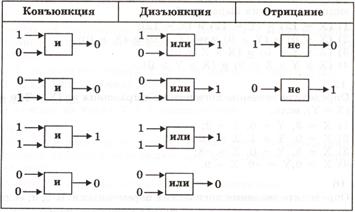
Рис 6.1 - Схематическое изображение логических операций

 

Пример. Для вычисления логического выражения: 1 или 0 и 1 нарисовать схему, от­ра­жающую последовательность выполнения логических операций. По схеме вычислить зна­чение логического выражения.

Решение.

 

Здесь наглядно отражено то, что первой выполняется операцияи, затемили. Теперь в порядке слева – направо припишем к выходящим стрелкам результаты операций:

В результате получилась1, т.е. «ИСТИНА».

Пример. Дано выражение:не (1 и (0 или 1) и 1).

Вычислить значение выражения с помощью логической схемы.

Решение. Логическая схема с результатами вычислений выглядит так:

 

Импликация и эквивалентность

Импликация(условное высказывание). В русском языке этой логической операции соответствуют союзы если ..., то; когда ..., тогда; коль скоро..., то и т. п.

Выражение, начинающееся после союзовесли, когда, коль скоро, называется основанием условного высказывания.

Выражение, стоящее после словто, тогда, называется следствием. В логических формулах операция импликации обозначается знаком «→». Импликация — двухместная операция; записывается так: А→В.

Эквивалентность. Языковой аналог — союзы если и только если; тогда и только тогда, когда ... Эквивалентность обозначаетсязнаком «≡» или «↔».

Порядоквсех пяти логических операций по убыванию старшинства следующий: отрица­ние, конъюнкция, дизъюнкция, импликация, эквивалентность.

Преобразование логических выражений

Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только при переменных.

Основные формулы преобразования логических выражений:

1.    A ≡ A

2.    (А & В) ≡ А   В.

3.    (А  В) ≡ А & В.

4.    (А → В) ≡А & В.

5.    А→B ≡ A  B.

6.    А ↔ В ≡ (А & В)  ( А & В) ≡ ( А  В) & (А   B).

7.    А & (А  B) ≡ А.

8.    А  А & В ≡ А.

9.    А & (А  В) ≡ А & В.

10. A   А & В ≡ А  В.

11. Законы коммутативности:

А & В ≡ В & А;

А  В ≡ В  А.

12. Законы ассоциативности:

(A  B)  С ≡ А  (В  С);

(А & В) & С ≡ А & (В & С).

13. Законы идемпотентности:

А  А ≡ А;

А & А ≡ А.

14. Законы дистрибутивности:

А & (В  С) ≡ (А & В)  (А & С);

А  (В & С) ≡ (А  В) & (А  С).

15. А  1 ≡ 1;

16. А & 1 ≡ А;

17. А  А ≡ 1;

18. А & 0 ≡ 0;

19. А & А ≡ 0.

6.3. Задание на лабораторную работу

Задания распределяются в зависимости от выданного преподавателем mn-кода. Если m — число нечетное, то ваш вариант 1, если четное — вариант 2.

Задание 1.Используя логические операции, запишите высказывания, которые являются истинными при выполнении следующих условий:

Вариант 1.  

1) хотя бы одно из чисел X, Y, Z положительно;

2) только одно из чисел X, Y, Z не является положительным.

3) только одно из чисел X, Y, Z больше 10

4) ни одно из чисел X, Y, Z не равно 104

Вариант 2.  

1) хотя бы одно из чисел X, Y, Z отрицательно;

2) только одно из чисел X, Y, Z является отрицательным.

3) только одно из чисел X, Y, Z не больше 10

4) каждое из чисел X, Y, Z равно 0

 

Задание 2.Определите значение логического выражения не (X>Z) ине (X=Y), если:

Вариант 1.  

1) X=3, Y=5, Z=2;

2) X=5, Y=0, Z=–8.

Вариант 2.

1) X=9, Y=–9, Z=9;

2) X=0, Y=1, Z=19.

 

Задание 3.Пусть a, b, c — логические величины, которые имеют следующие значения: а = истина, b= ложь, c = истина. Нарисуйте логические схемы для следующих логических выражений и вычислите их значения:

Вариант 1.  

1) а и b;

2) не а или b;

3) а илиb ис;

4) (а или b) и(c илиb).

Вариант 2.  

1) а или b;

2) а и b илис;

3) не а илиb ис;

4) не(а и b ис).

Задание 4.Построить логические схемы по логическому выражению:

Вариант 1. x₁ и (неx₂ или x₃).

Вариант 2. x₁ и x₂ или неx₁ и x₃.

 

Задание 5.Выполните вычисления по логическим схемам. Запишите соответствующие логические выражения:

Вариант 1.                                             Вариант 2.  

Задание 6.Дана логическая схема. Построить логическое выражение, соответствующее этой схеме.

 

Вычислить значение выражения для:

Вариант 1.  

1) x₁=0, x₂=1;

2) x₁=1, x₂=1.

Вариант 2.  

1) x₁=1, x₂=0;

2) x₁=0, x₂=0.

 

Задание 7.Дана логическая схема. Построить таблицу истинности для данной схемы.

               

  

Задание 8.Определить истинность формулы:

Вариант 1. ((a ) .

Вариант 2. .

 

Задание 9.Упростите выражение:

Вариант 1. .

Вариант 2. .

6.4. Требования к содержанию отчета

1. Цель лабораторной работы.

2. Задание на лабораторную работу. Mn – код.

3. Результаты решения заданий своего варианта.

4. Выводы по полученным результатам.

6.5. Контрольные вопросы

1. Что такое логическое высказывание, константа, переменная, формула?

2. Какие виды логических операций рассматриваются в лабораторной работе?

3. Таблицы истинности для импликации и эквивалентности?

4. Перечислите законы алгебры логики?

Лабораторная работа №7
"СИСТЕМЫ СЧИСЛЕНИЯ"

7.1. Цель работы

Изучение систем счисления. Приобретение навыков перевода из одной системы счи­с­ления в другую

7.2. Методические указания [2]

Развернутой формой записи числа называется запись в виде:

A_q=±(a _n-1 q ^n-1+ a _n-2 q ^n-2+…+ a₀ q⁰+ a _–1q ^-1 + a_-2 q^-2 + …+ а_-m q^-m).

Здесь А_q — само число, q — основание системы счисления, а_i — цифры данной системы счи­сления, n — число разрядов целой части числа, m — число разрядов дробной части чис­ла.

Пример. Получить развернутую форму десятичных чисел 32478; 26,387.

32478₁₀ = 3*10000 + 2*1000 + 4*100 + 7*10 + 8 = 3*10⁴ + 2*10³ + 4*10² + 7*10¹ + 8*10⁰.

26,387₁₀ = 2*10¹ + 6*10⁰ + 3*10^-1 + 8*10^-2 + 7*10^-3.

Пример. Получить развернутую форму чисел 112₃, 101101₂, 15FC₁₆, 101,11₂

 112₃=1*10² + 1*10¹ + 2*10⁰.

 1011012 = 1*10¹⁰¹ + 0*10¹⁰⁰ + 1*10¹¹ + 1*10¹⁰ + 0*10¹ + 1*10⁰.

15FC₁₆ = 1*10³ + 5 *10² + F*10¹ + С.

101,11₂ = 1*10¹⁰ + 0*10¹ + 1*10⁰ + 1*10^-1 + 1*10^-10.

Если все слагаемые в развернутой форме недесятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то по­лу­чится число в десятичной системе, равное данному. По этому принципу производится пе­ревод из недесятичной системы в десятичную.

Пример. Все числа из предыдущего примера перевести в десятичную систему.

112₃ =1*3² + 1*3¹ + 2*3⁰ = 9+3+2 = 14₁₀.

101101₂ = 1*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ =32+8+4+1 = 45₁₀,

15FC₁₆= 1*16³ + 5*16² + 15*16¹ + 12 = 4096 + 1280 + 240 + 12 = 5628₁₀.

101,11₂= 1*2² + 0*2¹ + 1*2⁰ + 1*2 ^–1 + 12^-2 = 4 + 1 + 1/2 + 1/4 = 5 + 0,5 + 0,25 = 5,75₁₀.

---

Дата добавления: 2018-04-15; просмотров: 11153; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!