Приклади виконання задач самостійної роботи №2
Приклад 2.2.1Розв’язати рівняння `
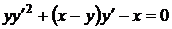(2.8)
Розв’язок:Розв’язавши це рівняння відносно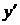 
будемо мати
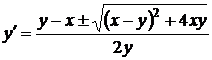
або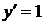 
, 
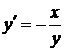, звідки 
, 
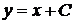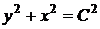
Приклад 2.2.2Розв’язати рівняння
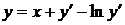(2.9)
та знайти особливий розв’язок.
Розв’язок:Вводимопараметр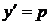 
,
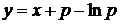(2.10)
Беремо повний диференціал від обох частин рівності (2.10) та замінюємо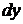 
на 
:
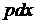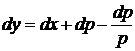або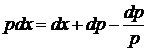 
Розв’язуємо отримане рівняння
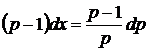(2.11)
а) Якщо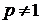 
, то скорочуємо на 
: 
, 
.
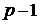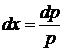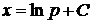Підставляючи це в (2.10), отримаємо розв’язок у параметричній формі
, 
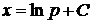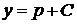(2.12)
В даному випадку розв’язок можна знайти в явному вигляді, виключаючи параметр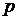 
з рівнянь (2.12)
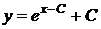(2.13)
б) Нехай в (2.11)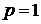 
. Підставляючи 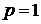в (2.10) отримаємо розв’язок 
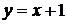. Знайдемо особливі розв’язки рівняння (2.9). Знайдемо похідну від обох його частин по :
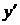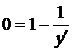(2.14)
Виключимо 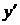з рівнянь (2.9), (2.14). З (2.14) маємо 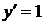, підставляючи це в (2.9) отримаємо рівняння дискримінантної кривої
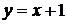(2.15)
Перевіримо, чи буде вона особливим розв’язком. Спочатку перевіряємо, чи є вона розв’язком рівняння (2.9). Підставляючи (2.15) в (2.9) отримаємо тотожність, тобто крива (2.15) - розв’язок.
|
|
|
Далі перевіримо, чи є цей розв’язок особовим, тобто чи дотикаються до нього в кожній точці інші розв’язки. Інші розв’язки описуються рівнянням (2.13). Запишемо умови дотику кривих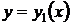 
и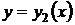 
в точці з абсцисою 
:
, 
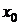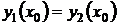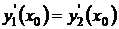(2.16)
Для розв’язків (2.13) та (2.15) ці умови набувають вигляду
, 
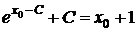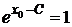
З другої рівності маємо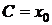 
, підставляючи це в першу рівність, отримаємо 
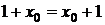. Ця рівність виконується при будь-яких 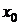. Значить, при кожному 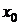розв’язок 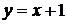в точці 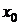дотикається до однієї з кривих сімейства (2.13), а саме до тієї кривої, для якої .
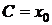Таким чином, в кожній точці розв’язок 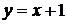дотикається до іншого розв’язку (2.13), який з ним не співпадає. Тому, розв’язок 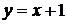- особливий.
Приклад 2.2.3Розв’язати рівняння Лагранжа
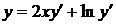(2.17)
Розв’язок:Покладемо 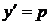. Тоді 
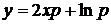. Диференціюючи, знаходимо 
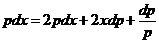. Звідки 
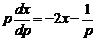, або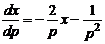 
. Отримали рівняння першого порядку, лінійне по 
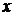. Розв’язуючи його, знаходимо 
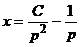. Підставляючи знайдене значення 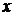в вираз для 
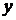, отримаємо
, 
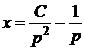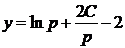
Приклад 2.2.4Розв’язати рівняння Клеро
, 
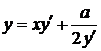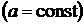(2.18)
Розв’язок:Покладаючи в(2.18) 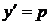, отримаємо
|
|
|
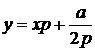(2.19)
Диференціюючи, знаходимо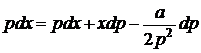 
, звідки 
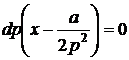. Дослідимо обидва множника:
1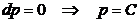 
. Загальний розв’язок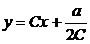 
2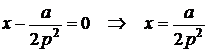 
Виключаючи 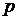з цього рівняння, та з рівняння (2.19), отримаємо 
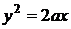. Це також розв’язок рівняння (2.18). Окрім того він є особливим розв’язком.
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
3.1 Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений.- М.: Наука, 1970.- 280 с.
3.2 Понтрягин Л.С. Обыкновенные дифференциальные уравнения.- М.: Наука, 1970.- 332 с.
3.3 Степанов В.В. Курс дифференциальных уравнений.- М.: Наука, 1958.- 468 с.
3.4 Матвеев Н.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям.- Минск: Вышейш. шк., 1987.- 320 с.
3.5 Киселев А.И., Краснов М.Л., Макаренко Г.И. Сборник задач по обыкновенным дифференциальным уравнениям.- М.: «Высшая школа», 1967.- 312 с.
3.6 Филиппов А.Ф. Сборник задач по дифференциальным уравнениям.- М.: Наука, 1985.- 128 с.
Дата добавления: 2018-04-15; просмотров: 217; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!