Диференційні рівняння з розділеними змінними
Диференційне рівняння вигляду
 (1.5)
(1.5)
називається рівнянням з розділеними змінними.
Загальний інтеграл рівняння знаходиться інтегруванням лівої та правої частин (1.5).
Диференційне рівняння вигляду
 (1.6)
(1.6)
де  - сталі, заміною змінних
- сталі, заміною змінних  перетворюється в рівняння з розділеними змінними.
перетворюється в рівняння з розділеними змінними.
При діленні обох частин рівняння на вираз, якій містить невідомі 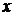 і
і 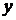 , можуть бути втрачені розв’язки, що перетворюють цей вираз в нуль.
, можуть бути втрачені розв’язки, що перетворюють цей вираз в нуль.
Однорідні диференційні рівняння, та рівняння, що до них зводяться
Однорідні диференційні рівняння можуть бути записані у вигляді
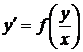 , (1.7)
, (1.7)
або
 , (1.8)
, (1.8)
де  і
і  - однорідні функції одного й того ж ступеня. Для розв’язання однорідного рівняння можна зробити заміну
- однорідні функції одного й того ж ступеня. Для розв’язання однорідного рівняння можна зробити заміну 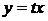 , яка приводить до рівняння зі змінними, що розділяються.
, яка приводить до рівняння зі змінними, що розділяються.
Рівняння вигляду
 (1.9)
(1.9)
зводиться до однорідного за допомогою перенесення початку координат в точку перетину прямих  і
і  . Якщо ці прямі не перетинаються, то
. Якщо ці прямі не перетинаються, то  . Рівняння набуває вигляду
. Рівняння набуває вигляду  і зводиться до рівняння зі змінними, що розділяються заміною
і зводиться до рівняння зі змінними, що розділяються заміною  або
або  .
.
Деякі рівняння можна звести до однорідних заміною  , де
, де  - число, яке треба визначити з умови, щоб рівняння було однорідним. Якщо
- число, яке треба визначити з умови, щоб рівняння було однорідним. Якщо  не знаходиться з цієї умови, то рівняння не можна звести до однорідного вказаним способом.
не знаходиться з цієї умови, то рівняння не можна звести до однорідного вказаним способом.
Лінійні рівняння першого порядку. Рівняння Бернуллі та Ріккаті
|
|
|
Рівняння вигляду
 (1.10)
(1.10)
називається лінійним. Щоб його розв’язати потрібно спочатку розв’язати рівняння
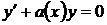 (1.11)
(1.11)
і в загальному розв’язку, замінити довільну сталу 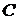 на невідому функцію
на невідому функцію 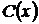 . Потім вираз, отриманий для
. Потім вираз, отриманий для 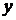 , підставити в рівняння (1.10) і знайти функцію
, підставити в рівняння (1.10) і знайти функцію 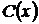 .
.
Деякі рівняння стають лінійними, якщо поміняти місцями функцію та незалежну змінну.
Для розв’язання рівняння Бернуллі
 ,
,  (1.12)
(1.12)
треба обидві його частини поділити на  і зробити заміну
і зробити заміну  , після чого отримаємо лінійне рівняння.
, після чого отримаємо лінійне рівняння.
Рівняння Рікатті
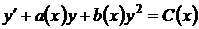 (1.13)
(1.13)
в загальному випадку не розв’язується в квадратурах. Якщо відомий один частинний розв’язок  , заміною
, заміною 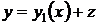 рівняння Рікатті зводиться до рівняння Бернуллі. Іноді частинний розв’язок можна підібрати виходячи з вигляду вільного члену рівняння.
рівняння Рікатті зводиться до рівняння Бернуллі. Іноді частинний розв’язок можна підібрати виходячи з вигляду вільного члену рівняння.
Рівняння в повних диференціалах. Інтегруючий множник
Диференційне рівняння вигляду
 (1.14)
(1.14)
називається рівнянням в повних диференціалах, якщо його ліва частина є повний диференціал деякої функції 

Необхідною та достатньою умовою того, що рівняння (1.14) - рівняння в повних диференціалах є умова ( в деякій області  зміни
зміни 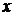 та
та 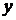 ). Загальний інтеграл рівняння (1.14) має вигляд
). Загальний інтеграл рівняння (1.14) має вигляд
|
|
|

або
 (1.15)
(1.15)
При інтегруванні деяких диференційних рівнянь можна згрупувати члени так, що отримуються комбінації, які легко інтегруються.
В деяких випадках, коли рівняння (1.14) не є рівнянням в повних диференціалах, все ж вдається підібрати функцію  , після множення на яку ліва частина (1.14) перетворюються на повний диференціал
, після множення на яку ліва частина (1.14) перетворюються на повний диференціал
 (1.16)
(1.16)
Така функція  називається інтегруючим множником.
називається інтегруючим множником.
Індивідуальні завдання
1Для даного диференційного рівняння методом ізоклін побудувати інтегральну криву, яка проходить через точку  , згідно варіанту:
, згідно варіанту:
1.6.1  , , 
| 1.6.2 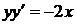 , , 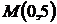
|
1.6.3  , , 
| 1.6.4  , , 
|
1.6.5 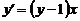 , , 
| 1.6.6  , , 
|
1.6.7 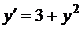 , , 
| 1.6.8  , , 
|
1.6.9  , , 
| 1.6.10  , , 
|
1.6.11  , , 
| 1.6.12  , , 
|
1.6.13  , , 
| 1.6.14  , , 
|
1.6.15 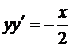 , , 
| 1.6.16  , , 
|
1.6.17  , , 
| 1.6.18  , , 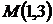
|
1.6.19  , , 
| 1.6.20  , , 
|
2 Визначити тип диференціального рівняння та знайти його загальний інтеграл, згідно варіанту
1.6.1 
| 1.6.3 
|
1.6.3 
| 1.6.4 
|
1.6.5 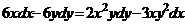
| 1.6.6  . .
|
1.6.7 
| 1.6.8 
|
1.6.9 
| 1.6.10 
|
1.6.11 
| 1.6.12 
|
1.6.13 
| 1.6.14 
|
1.6.15 
| 1.6.16 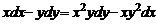
|
1.6.17 
| 1.6.18 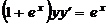
|
1.6.19 
| 1.6.20 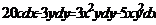
|
3 Визначити тип диференційного рівняння та знайти його загальний інтеграл, згідно варіанту:
1.6.1 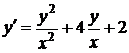
| 1.6.2 
|
1.6.3 
| 1.6.4 
|
1.6.5 
| 1.6.6 
|
1.6.7 
| 1.6.8 
|
1.6.9 
| 1.6.10 
|
1.6.11 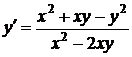
| 1.6.12 
|
1.6.13 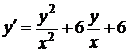
| 1.6.14 
|
1.6.15 
| 1.6.16 
|
1.6.17 
| 1.6.18 
|
1.6.19 
| 1.6.20 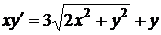
|
|
|
|
4 Визначити тип диференційного рівняння та знайти його загальний інтеграл, згідно варіанту:
1.6.1 
| 1.6.2 
|
1.6.3 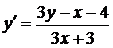
| 1.6.4 
|
1.6.5 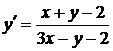
| 1.6.6 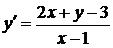
|
1.6.7 
| 1.6.8 
|
1.6.9 
| 1.6.10 
|
1.6.11 
| 1.6.12 
|
1.6.13 
| 1.6.14 
|
1.6.15 
| 1.6.16 
|
1.6.17 
| 1.6.18 
|
1.6.19. 
| 1.6.20 
|
5 Визначити тип диференційного рівняння та розв’язати задачу Коші, згідно варіанту:
1.6.1  , , 
| 1.6.2  , , 
|
1.6.3  , , 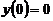
| 1.6.4  , , 
|
1.6.5  , , 
| 1.6.6  , , 
|
1.6.7  , , 
| 1.6.8  , , 
|
1.6.9  , , 
| 1.6.10 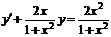 , ,

|
1.6.11  , , 
| 1.6.12  , , 
|
1.6.13  , , 
| 1.6.14  , , 
|
1.6.15  , , 
| 1.6.16  , , 
|
1.6.17  , , 
| 1.6.18 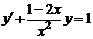 , , 
|
1.6.19  , , 
| 1.6.20  , ,

|
6 Визначити тип диференційного рівняння та розв’язати задачу Коші, згідно варіанту:
1.6.1  ,. ,. 
|
1.6.2  , , 
|
1.6.3  , , 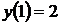
|
1.6.4 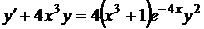 , , 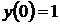
|
1.6.5  , , 
|
1.6.6  , , 
|
1.6.7  , , 
|
1.6.8 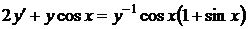 , , 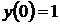
|
1.6.9  , , 
|
1.6.10  , , 
|
1.6.11  , , 
|
1.6.12  , , 
|
1.6.13 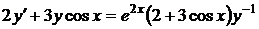 , , 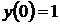
|
1.6.14  , , 
|
1.6.15  , , 
|
1.6.16  , , 
|
1.6.17  , , 
|
1.6.18  , , 
|
1.6.19  , , 
|
1.6.20  , , 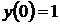
|
7 Визначити тип диференційного рівняння та розв’язати задачу Коші, згідно варіанту:
1.6.1  ,. ,. 
|
1.6.2  , , 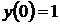
|
1.6.3 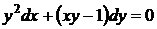 , , 
|
1.6.4  , , 
|
1.6.5  , , 
|
1.6.6  , , 
|
1.6.7  , , 
|
1.6.8  , , 
|
1.6.9  , , 
|
1.6.10  , , 
|
1.6.11  , , 
|
1.6.12 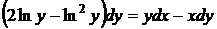 , , 
|
1.6.13  , , 
|
1.6.14  , , 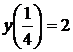
|
1.6.15  , , 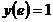
|
1.6.16  , , 
|
1.6.17  , , 
|
1.6.18 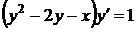 , , 
|
1.6.19  , , 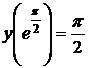
|
1.6.20  , , 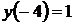
|
|
|
|
8 Знайти загальний розв’язок диференційного рівняння, згідно варіанту:
1.6.1 
|
1.6.2 
|
1.6.3 
|
1.6.4 
|
1.6.5 
|
1.6.6 
|
1.6.7 
|
1.6.8 
|
1.6.9 
|
1.6.10 
|
1.6.11 
|
1.6.12 
|
1.6.13 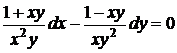
|
1.6.14 
|
1.6.15 
|
1.6.16 
|
1.6.17 
|
1.6.18 
|
1.6.19 
|
1.6.20 
|
Дата добавления: 2018-04-15; просмотров: 352; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
