Рівняння, які не розв’язані відносно похідної. Рівняння Лагранжа та Клеро. Особливі розв’язки
Рівняння, не розв’язані відносно похідної в загальному випадку мають вигляд
(2.1)
Методи розв’язування таких рівнянь залежать від їх вигляду:
а) розв’язати рівняння відносно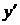 
, тобто з рівняння (2.1) виразити 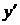через 
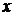та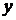 
. Отримаємо одне чи декілька рівнянь вигляду 
, кожне з яких розв’язується окремо;
б) метод введення параметру. Нехай рівняння (2.1) можна розв’язати відносно 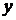, тобто записати у вигляді 
. Вводячи параметр
(2.2)
отримаємо
(2.3)
Обчислимо повний диференціал від обох частин рівності (2.3) та замінімо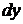 
на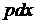 
Якщо розв’язок цього рівняння знайдено у вигляді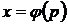 
, то скориставшись рівністю (2.3), отримаємо розв’язок вихідного рівняння в параметричному запису
, 
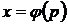З допомогою цього ж методу розв’язуються рівняння вигляду 
;
в) рівняння Лагранжа має вигляд
(2.4)
Покладаючи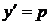 
, методом диференціювання з заміною 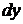на 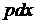, зводимо це рівняння до лінійного відносно 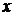, як функції 
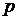. Нехай 
розв’язок лінійного рівняння. Тоді загальний розв’язок рівняння Лагранжа у параметричній формі має вигляд
, 
;
г) рівняння Клеро має вигляд
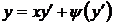(2.5)
Для розв’язання рівняння (2.5) використовується той самий метод, що й для рівняння Лагранжа. Загальний розв’язок має вигляд 
.
|
|
|
Розв’язок 
диференціального рівняння (2.1) називається особливим, якщо у кожній його точці порушується властивість єдиності, тобто через кожну його точку 
, окрім цього розв’язку проходить і іншій розв’язок, який має в точці ту ж саму дотичну, що й розв’язок але не співпадає з ним в досить малому околі . Графік особливого розв’язку називається особовою інтегральною кривою рівняння (2.1). Якщо функція 
та її часткові похідні 
і 
неперервні за всіма аргументами 
, то будь-який особливий розв’язок рівняння (2.1) задовольняє також рівнянню
(2.6)
Таким чином, для того щоб знайти особливі розв’язки рівняння (2.1) треба вилучити 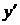з рівнянь (2.1), (2.6). Отримане в результаті цього рівняння
(2.7)
називається 
- дискримінантом рівняння (2.1), а крива (2.7) називається - дискримінантною кривою. Часто - дискримінантна крива розпадається на декілька гілок. Тоді треба перевірити, чи є кожна окрема гілка розв’язком рівняння (2.1) і якщо є, чи буде він особливим, тобто чи порушується його єдиність в кожній точці.
|
|
|
Індивідуальні завдання
1 Знайти загальнийрозв’язок диференційного рівняння, згідно варіанту:
2.1.1 
| 2.1.2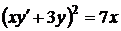 
|
2.1.3 
| 2.1.4 
|
2.1.5 
| 2.1.6 
|
2.1.7 
| 2.1.8 
|
2.1.9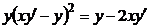 
| 2.1.10 
|
2.1.11 
| 2.1.12 
|
2.1.13 
| 2.1.14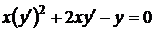 
|
2.1.15 
| 2.1.16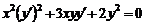 
|
2.1.17 
| 2.1.18 
|
2.1.19 
| 2.1.20 
|
2 Знайти загальнийрозв’язок диференційного рівняння, згідно варіанту:
2.1.1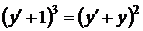 
| 2.1.2 
|
2.1.3 
| 2.1.4 
|
2.1.5 
| 2.1.6 
|
2.1.7 
| 2.1.8 
|
2.1.9 
| 2.1.10 
|
2.1.11 
| 2.1.12 
|
2.1.13 
| 2.1.14 
|
2.1.15 
| 2.1.16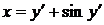 
|
2.1.17 
| 2.1.18 
|
2.1.19 
| 2.1.20 
|
3 Знайти загальнийрозв’язок диференційного рівняння, згідно варіанту:
2.1.1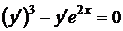 
| 2.1.2 
|
2.1.3 
| 2.1.4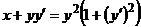 
|
2.1.5 
| 2.1.6 
|
2.1.7 
| 2.1.8 
|
2.1.9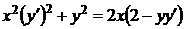 
| 2.1.10 
|
2.1.11 
| 2.1.12 
|
2.1.13 
| 2.1.14 
|
2.1.15 
| 2.1.16 
|
2.1.17 
| 2.1.18 
|
2.1.19 
| 2.1.20 
|
4 Знайти загальний розв’язок диференційного рівняння, згідно варіанту:
2.1.1 
| 2.1.2 
|
2.1.3 
| 2.1.4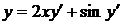 
|
2.1.5 
| 2.1.6 
|
2.1.7 
| 2.1.8 
|
2.1.9 
| 2.1.10 
|
2.1.11 
| 2.1.12 
|
2.1.13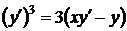 
| 2.1.14 
|
2.1.15 
| 2.1.16 
|
2.1.17 
| 2.1.18 
|
2.1.19 
| 2.1.20 
|
5 Знайти лінію, яка проходить через т. 
і таку, що в будь-якій її точці 
нормальний вектор 
з кінцем на вісі 
, має довжину, яка дорівнює 
, та утворює гострий кут з додатнім напрямом вісі .
2.1.1  , 
| 2.1.2  , 
|
2.1.3  , 
| 2.1.4  , 
|
Знайти лінію, яка проходить через т. , якщо відрізок будь-якої нормалі, який знаходиться між віссю 
віссю та ділиться точкою лінії у відношенні 
(рахуючи від вісі ).
|
|
|
2.1.5  ,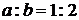 
| 2.1.6  , 
|
2.1.7  , 
| 2.1.8  , 
|
Знайти лінію, яка проходить через т. , якщо відрізок будь-якої її дотичної, який знаходиться між точкою дотику віссю , ділиться в точці дотику з віссю абсцис у відношенні (рахуючи від вісі ).
2.1.9  , 
| 2.1.10  , 
|
2.1.11  , 
| 2.1.11.  ,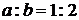
|
Знайти лінію, яка проходить через т. , якщо відрізок будь-якої її дотичної, який знаходиться між віссю та віссю , ділиться в точці дотику у відношенні (рахуючи від вісі ).
| 2.1.13 ,
| 2.1.14 , 
|
2.2.15  ,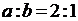 
| 2.1.16  , 
|
Знайти лінію, яка проходить через т. і володіє властивістю, що в будь-якій точці дотичний вектор з кінцем на вісі має проекцію на вісь , яка дорівнює .
2.1.17 , 
| 2.1.18  ,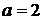 
|
2.1.19  , 
| 2.1.20  , 
|
Дата добавления: 2018-04-15; просмотров: 312; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!