Приклади виконання задач самостійної роботи №1

 

Приклад 1.7.1За допомогою ізоклін побудувати інтегральні криві рівняння

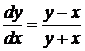
Розв’язок:Покладемо 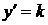, отримаємо рівняння сімейства ізоклін .

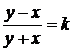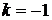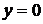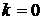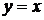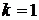Таким чином, ізоклінами є прямі, які проходять через початок координат. При  отримаємо ізокліну , при  - ізокліну , при  = ізокліну 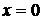. Розглядаючи перевернуте рівняння  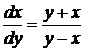знайдемо ізокліну 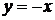, у всіх точках якої інтегральні криві мають вертикальні дотичні. За допомогою отриманих ізоклін будуємо інтегральні криві, як на рис.1.

 

 

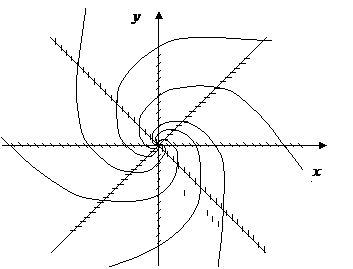Рисунок 1.1 – Наближений графік розв’язку рівняння

 

Приклад 1.7.2Розв’язати рівняння

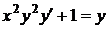                                                (1.17)

Розв’язок:Перетворимо рівняння (1.17) до вигляду

 =>

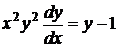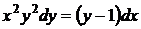
Ділимо обидві частини рівняння на 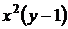. Отримаємо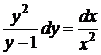

Змінні розділені. Інтегруємо обидві частини

 =>

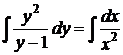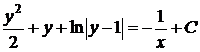
При діленні на 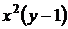 могли бути втрачені розв’язки  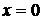і 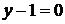. Перевіркою з’ясовуємо, що  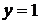- є розв’язком рівняння (1.17), а  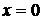-ні.

 

Приклад 1.7.3Знайти розв’язок рівняння

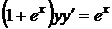,                                                 (1.18)

який задовольняє початковій умові

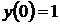                                                               (1.19)

Розв’язок:Маємо 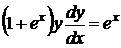. Інтегруючи останнє рівняння, отримуємо

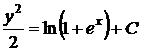                                           (1.20)

Вважаючи в (1.20) 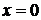, будемо мати 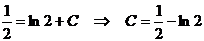. Підставляючи С в (1.20), отримаємо  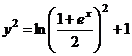 або .

 

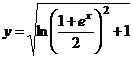Приклад 1.7.4Знайти розв’язок задачі Коші

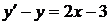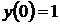,                          (1.21)

Розв’язок:Приведемо рівняння до вигляду 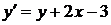 та зробимо заміну змінних 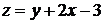. Тоді 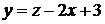,  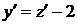і рівняння набуває вигляду .

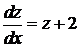Розділяємо змінні 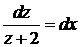 та інтегруємо  => => .

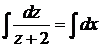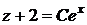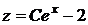Повертаємось до старої змінної 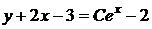,  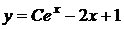- загальний розв’язок рівняння (1.21).

Знайдемо розв’язок в точці 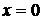, 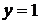: 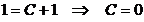. Отже, частинний розв’язок має вигляд .

 

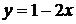Приклад 1.7.5Розв’язати рівняння

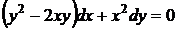                                   (1.22)

Розв’язок:Функції 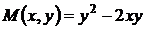,  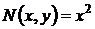мають другий ступень, тому рівняння однорідне. Покладемо 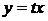. Тоді 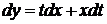. Підставляючи в (1.22), отримаємо => .

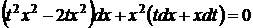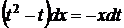Розділяємо змінні 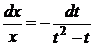 та інтегруємо  =>  =>

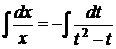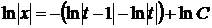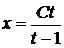
Повертаючись до старої змінної, отримаємо загальний інтеграл рівняння .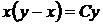

Окрім того, маємо розв’язок 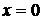, який було втрачено при діленні на .

 

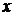Приклад 1.7.6Розв’язати рівняння

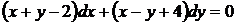                                        (1.23)

Розв’язок:Знайдемо точку перетину прямих

,

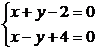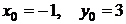
Зробимо заміну змінних 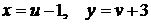. Рівняння (1.23) набуде вигляду

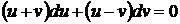                                          (1.24)

Рівняння (1.24) є однорідним. Покладемо 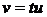. Отримаємо 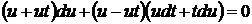. Звідки 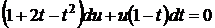. Розділимо змінні 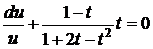. Інтегруючи, знаходимо , .

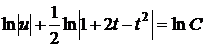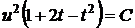Повертаємось до змінних :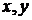

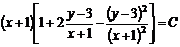, або

 

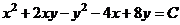
Приклад 1.7.7Розв’язати рівняння

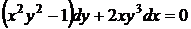                                        (1.25)

Розв’язок:Зробимо підстановку 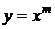, 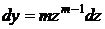. Підставимо в (1.25)

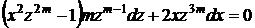 або .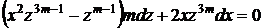

Рівняння буде однорідним, якщо ступені усіх доданків однакові 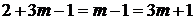. Звідки 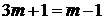, 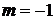. Отже, маємо  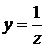і рівняння (1.25) набуває вигляду 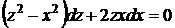, яке є однорідним. Покладемо 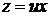. Тоді 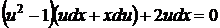, або .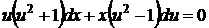

Розділюючи змінні, отримуєм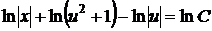о  або .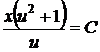

Повертаючись до старих змінних, отримуємо загальний інтеграл рівняння (1.25)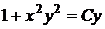

 

Приклад 1.7.8Розв’язати рівняння

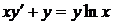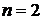,                               (1.26)

Розв’язок:Зробимо заміну змінних .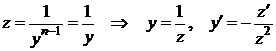

Рівняння (1.26) набуде вигляду 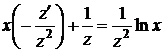, або

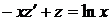                                                           (1.27)

Рівняння (1.27) – лінійне неоднорідне. Відкидаючи праву частину, розв’язуємо лінійне однорідне рівняння

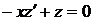                                                                (1.28)

Розділимо змінні 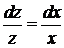. Інтегруючи, отримуємо  => =>

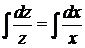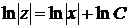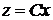
Вважаючи 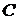 функцією, залежною від 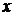, застосовуємо метод варіації довільної сталої.

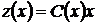                                                               (1.29)

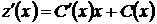                                                (1.30)

Підставимо (1.29), (1.30) у рівняння (1.26)

=>  => .

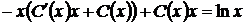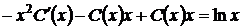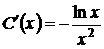Звідки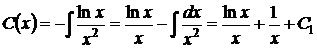

Підставимо 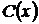 в рівняння (1.29) та одержимо загальний розв’язок лінійного неоднорідного рівняння (1.27). Повернемося до змінної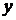

.

 

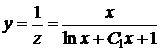Приклад 1.7.9Розв’язати рівняння ік каті

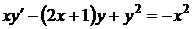                               (1.31)

Розв’язок:Знайдемо частинний розв’язок рівняння ік каті 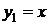 і зробимо заміну змінних

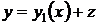                                                                          (1.32)

Підставимо (1.32) в рівняння (1.31)

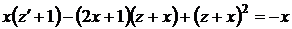, або

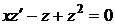                                                           (1.33)

Одержали рівняння Бернуллі з 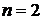. Зробимо заміну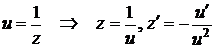

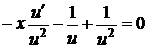 або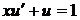

Знайдемо розв’язок лінійного неоднорідного рівняння.

,

 =>

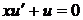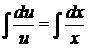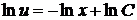
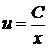                                                                           (1.34)

Застосуємо метод варіації довільної сталої

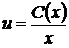                                                                      (1.35)

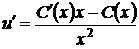
Підставимо 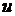 і 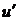 в лінійне неоднорідне рівняння

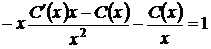
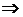
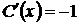
Інтегруючи, одержимо

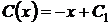                                                           (1.36)

Підставляючи (2.36) в рівняння (1.35) одержимо загальний розв’язок лінійного неоднорідного рівняння

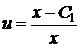                                                                   (1.37)

Послідовно повертаємось до змінних 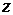 та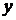

,

.

 

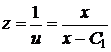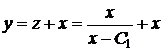Приклад 1.7.10Знайти загальний розв’язок рівняння

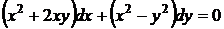                     (1.38)

Розв’язок: 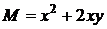, 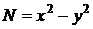. Перевіримо виконання умови 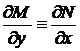: 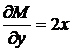, 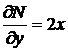. Умова виконується. Знаходимо загальний розв’язок рівняння (1.38)

 

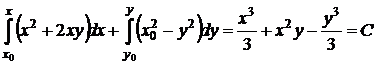
Приклад 1.7.11Знайти загальний розв’язок рівняння

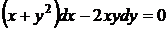                                   (1.39)

Розв’язок: 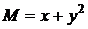, 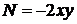. Перевіримо виконання умови 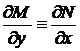: 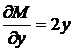, 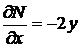. Умова не виконується. Підберемо інтегруючий множник, так щоб виконалася умова 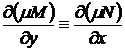, або 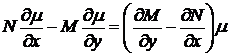. Звідки

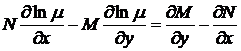                           (1.40)

Припустимо, що 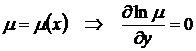 і рівняння (1.39) набуває вигляду

.

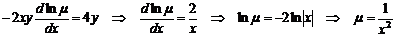Рівняння 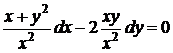 є рівнянням в повних диференціалах. Його ліву частину можна звести до вигляду 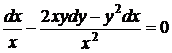. Звідки  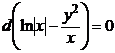і загальний інтеграл даного рівняння є .

 

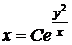Самостійна робота № 2

 

---

Дата добавления: 2018-04-15; просмотров: 614; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!