Собственные векторы и собственные значения матриц. Оценка однородности суждений
Собственные векторы и значения матриц
Ранжирование элементов, анализируемых с использованием матрицы парных сравнений [E], осуществляется на основании главных собственных векторов, получаемых в результате обработки матриц.
Вычисление главного собственного вектора W положительной квадратной матрицы [E] проводится на основании равенства
EW=λmaxW, (2.1)
где λmax — максимальное собственное значение матрицы [Е].
Для положительной квадратной матрицы [Е] правый собственный вектор W, соответствующий максимальному собственному значению λmax, с точностью до постоянного сомножителя С можно вычислить по формуле
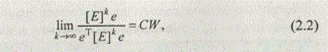
гдее={1,1,1, ....l}Т – единичный вектор;
k = 1, 2, 3, ... — показатель степени;
С— константа;
Т — знак транспонирования.
Вычисления собственного вектора W по выражению (2.2) производятся до достижения заданной точности:
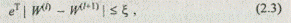
где l — номер итерации, такой, что l = 1 соответствует k = 1; l = 2, k = 2;
l = 3, k = 4 и т. д.;
ξ — допустимая погрешность.
С достаточной для практики точностью можно принять x = 0,01 независимо от порядка матрицы.
Максимальное собственное значение вычисляется по формуле:
λmax=eT[E]W
Динамические предпочтения и приоритеты
Задача прогнозирования экспертных предпочтений связана с получением оценок приоритетности альтернатив в форме зависимостей от времени. Для этого исходные экспертные оценки должны содержать информацию об изменении предпочтительности одной альтернативы перед другой на некотором временном отрезке. Следовательно, оценка предпочтительности может быть задана не константой, а функцией. Подбор таких функций можно осуществить, либо предоставив в распоряжение эксперта некоторую функциональную шкалу [2], либо путем аппроксимации экспертных оценок, полученных в различные моменты времени. Пример функциональной шкалы показан в табл. 2.2, где функции предпочтительности содержат параметры, подбор которых позволяет более или менее точно описать изменяющиеся суждения и установить область допустимых значений функций в пределах девятибалльной шкалы (см. табл. 2.1).
|
|
|
Таблица 2.2
Динамические суждения
| Вид функции | Описание функции | Примечание |
| const | Для всех t l £ const £ 9 | Постоянство предпочтений |
| a1(t)+a2 | Линейная функция от t на некотором отрезке, обратная функция - гипербола | Линейное возрастание предпочтения одной альтернативы перед другой во времени |
| b1ln(t+1)+b2 | Логарифмический рост | Быстрое возрастание предпочтения одной альтернативы перед другой до некоторого t, после которого следует медленное возрастание |
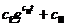
| Экспоненциальный рост или убывание (с2<0), в последнем случае обратная величина – S-образная логистическая кривая | Медленное увеличение или уменьшение предпочтения во времени, за которым следует быстрое увеличение (уменьшение) |
| d1t2+d2t+d3 | Парабола с максимумом или минимумом в зависимости оттого, отрицательно или положительно d1. | Возрастание до максимума, а затем убывание (или наоборот) |
| f1tnsin(t+f2)+f3 | Колебательная функция | Колебания предпочтений во времени с возрастающей (п>0)или убывающей (n≤0) амплитудой |
| Катастрофы | Функции, имеющие разрывы, которые следует указать | Крайне резкие изменения интенсивности предпочтений |
|
|
|
Эти функции отражают интуитивные чувства лица, принимающего решения об изменении в тренде: постоянном, линейном, логарифмическом и экспоненциальном, возрастающем до максимума и убывающем или опускающемся до минимума и возрастающем, колебательном и, наконец, допускающем катастрофические изменения.
Для динамических задач матрица парных сравнений содержит функции времени в качестве элементов, поэтому максимальное собственное число λmax, также собственный вектор W также будут зависеть от времени, т. е.
|
|
|
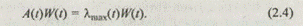
Здесь A(t) — матрица парных сравнений объектов, содержащая информацию об изменении предпочтительности одной альтернативы перед другой на некотором промежутке времени, которая задана функцией из табл. 2.2.
Если порядок матрицы парных сравнений не превышает четырех, для уравнения (2.4) можно получить аналитическое решение [2]. Альтернативным способом является получение A(t) и W(t) численными методами. Для этого необходимо иметь в распоряжении информацию о предпочтениях экспертов за определенный период времени. При накапливании такой информации в компьютерной системе становятся возможными прогнозирование предпочтений и оценка ближайших последствий принимаемых решений.
Оценка однородности суждений
В практических задачах количественная (кардинальная) и транзитивная (порядковая) однородность (согласованность) нарушается, поскольку человеческие ощущения нельзя выразить точной формулой. Для улучшения однородности в числовых суждениях, какая бы величина aij ни была взята для сравнения i-го элемента с j-м, aij приписывается значение обратной величины, т. е. аij = 1/aij. Отсюда следует, что если один элемент в а раз предпочтительнее другого, то последний только в 1/а раз предпочтительнее первого.
|
|
|
При нарушении однородности ранг матрицы отличен от единицы и она будет иметь несколько собственных значений. Однако при небольших отклонениях суждений от однородности одно из собственных значений будет существенно больше остальных и приблизительно равно порядку матрицы. Таким образом, для оценки однородности суждений эксперта необходимо использовать отклонение величины максимального собственного значения λmax от порядка матрицы п.
Однородность суждений оценивается индексом однородности (ИО) или отношением однородности (OO) в соответствии со следующими выражениями:
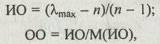
где М(ИО) — среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений [E], которое основано на экспериментальных данных (табл. 2.3), полученных в работе [2].
Таблица 2.3
Дата добавления: 2018-04-15; просмотров: 501; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
