Сравнение объектов методом копирования

В третьей модификации рассматривается определение вектора приоритетов альтернатив методом копирования.

Метод копирования применяется в тех случаях, когда среди анализируемых альтернатив имеются такие, которые идентичны по одним или нескольким анализируемым свойствам (критериям качества). Например, пневматическая виброзащитная система рукавного типа, используемая в рессорном подвешивании пассажирских автобусов, идентична по качеству виброизоляции с металлическим механизмом перескока, реализующим квазинулевую жесткость.

Рассмотрим процедуры сравнения и установления приоритета альтернатив, используемые в методе копирования.

Пусть определено множество альтернатив А = {а₁, а₂, ..., а_n}, каждая из которых отличается от всех других альтернатив этого множества уровнем качества по рассматриваемому критерию К_i и определено другое множество альтернатив В == {b₁, b₂, ..., b_n}, каждая из которых имеет одинаковые свойства со всеми другими по ранее определенному критерию К_i. Предположим, что множество А имеет хотя бы один элемент а_i^* , свойство которого по критерию К_i идентично свойствам всех альтернатив множества В. Тогда все альтернативы множества В являются копиями элемента а_i^* по критерию К_i. При такой ситуации эксперт по критерию К_i попарно сравнивает только альтернативы множества А. Далее на основании матрицы попарных сравнений рассчитывается нормированный собственный вектор W^A, ранжирующий альтернативы множества A. Всем альтернативам-копиям {b₁, b₂, ..., b_n} присваивается значение нормированного собственного вектора W^A, соответствующее элементу a_i^*. В результате получается новый ненормированный вектор приоритетов W^AB всех альтернатив, входящих в множества A и В. Вектор W^AB нормируется путем деления каждого значения указанного вектора на сумму всех его значений.

Метод копирования аналогичен методу сравнения альтернатив относительно стандартов в том плане, что позволяет не нарушать порядок ранее проранжированных альтернатив при добавлении новых, являющихся копиями ранее проранжированных альтернатив. Кроме того, число анализируемых альтернатив при добавлении копий может превышать пороговое значение, равное девяти, установленное для метода попарного сравнения.

Рассмотрим пример добавления к ранее проранжированным объектам альтернатив-копий.

Допустим, определены три альтернативы A₁, А₂ и А₃, для которых экспертом установлена относительная степень предпочтений по критерию "надежность функционирования системы". Альтернативы сравниваются попарно в матрице, для которой рассчитывается нормированный собственный вектор, имеющий значения {0,5 0,3 0,2}^T . В приведенном векторе указан знак транспонирования — Т, а порядок значений вектора соответствует весу альтернатив А₁, А₂ и А₃. Предположим, что для анализа поступают две новые альтернативы А₄, А₅, свойства которых по указанному критерию полностью идентичны свойствам альтернативы А₃. В этом случае альтернативам-копиям присваиваются веса, соответствующие весу альтернативы А₃,, т. е. А₄ = 0,2 и А₅ = 0,2. Новый ненормированный вектор приоритетов альтернатив принимает следующий вид:

{0,5 0,3 0,2 0,2 0,2}^T

Значения весов пяти альтернатив после нормирования предыдущего вектора приоритетов имеют следующий вид:

A₁ = 0,35, А₂ == 0,21, А₃ = 0,14, A₄ = 0,14, A₅= 0,14.

Анализ двух векторов приоритетов, характеризующих соответственно множества из трех и пяти альтернатив, показывает, что добавление альтернатив А₄, А₅ не нарушило порядок приоритетности альтернатив А₁, А₂ и А₃,.

Метод копирования позволяет существенно сократить время экспертов на подготовку исходных данных для анализа и уменьшить вероятность внесения в них как случайных, так и логических ошибок.

Многокритериальный выбор на иерархиях с различным числом и составом альтернатив под критериями

В четвертой модификации рассматривается метод определения векторов приоритетов альтернатив для иерархий с различным числом и различающимся составом альтернатив под критериями.

В практике принятия решений нередко встречается задача, когда ранжируемые по множеству критериев альтернативы оцениваются экспертом не по всем критериям. Эта задача характерна для ситуаций, в которых множество критериев, выделенных для всех рассматриваемых альтернатив, является избыточным относительно одной или нескольких альтернатив. Таким образом, в рассматриваемом случае эксперт имеет разное количество альтернатив под каждым критерием или под их частью. На рис. 2.7 приведены примеры иерархий, в которых каждый критерий E_j из множества {Е₁, E₂, ... , Е_p} имеет разное количество альтернатив из множества {А₁,А₂, ... ,А_r}.

Альтернативы А₁ и А_r; А₁, А₂ А_r; А₂ и А_r оцениваются соответственно относительно элементов (критериев) Е₁, Е₂, Е_р (рис. 2.7а).

Рис. 2.7. Примеры иерархий с разным числом альтернатив под критериями а — синтез; б — декомпозиция

Рассмотрим методику определения вектора приоритета альтернатив для случая, когда иерархия имеет один уровень критериев, объединенных фокусом (рис. 2.7 б) с учетом значимости критериев, и разное количество альтернатив у каждого критерия. Методика предполагает выполнение ряда процедур по структурированию информации и проведению вычислительных операций.

Процедура 1. Исходная проблема структурируется в виде иерархии, устанавливающей взаимосвязь между множеством сравниваемых альтернатив {А₁, A₂,... , А_r}и множеством критериев {E₁, Е₂, ... , Е_p}.

Процедура 2. На основе иерархической структуры определяется бинарная матрица [В], устанавливающая соответствие между альтернативами и критериями. Матрица [В] содержит элементы b_ij = {0,1}. При этом если альтернатива А_i оценивается по критерию E_j, то b_ij = 1, в противном случае b_ij = 0.

Процедура 3. Осуществляется экспертная оценка альтернатив по соответствующим критериям. Для этой цели используются метод попарного сравнения, метод сравнения относительно стандартов или метод копирования. На основе экспертных оценок с учетом матрицы [В] строится матрица [А] следующего вида:

В матрице [А] экспертные оценки {a_ij} представляют векторы приоритетов альтернатив относительно критериев E_j. При этомеслиальтернативаА_i не оценивается по критерию Е_j, то в матрице [А] соответствующее значение a_ij = 0. Векторы в указанной матрице имеют различное число значений a_ij и могут быть нормированными или ненормированными в зависимости от используемого метода сравнения альтернатив.

Процедура 4. В результате обработки матрицы попарных сравнений критериев Е_j определяется нормированный вектор приоритетов критериев .

Процедура 5. Формируются структурные критерии S и L, отображаемые соответствующими диагональными матрицами [S] и [L].

Рассмотрим состав упомянутых матриц.

Матрица [S] имеет следующий вид:

где a_ij — значения векторов приоритетов из матрицы [А].

С помощью матрицы [S] обеспечивается нормирование векторов приоритетов альтернатив, образующих матрицу [А], если последняя заполнена методом сравнения относительно стандартов или копирования без предварительного нормирования.

Матрица [L] имеет следующий вид:

где R_j — число альтернатив А_i, находящихся под критерием Е_j,

— суммарное число альтернатив, находящихся под всеми критериями.

Здесь следует отметить, что число N в матрице [L] может приниматься равным числу рассматриваемых альтернатив r, т.е. N= r. При этом на конечный результат способ определения N не оказывает влияния.

Использование структурного критерия L позволяет эксперту или ЛПР изменять при необходимости вес альтернатив, связанных с соответствующими критериями пропорционально отношению R_j / N. Этим обеспечивается повышение приоритета альтернатив, образующих большие группы, и снижение приоритета альтернатив в группах с их относительно небольшим числом. Здесь имеется в виду, что группу определяют альтернативы, являющиеся "потомками" по отношению к критерию E_j. Необходимость в приведенной вычислительной процедуре обусловлена тем, что у критериев-"родителей" с высоким приоритетом в иерархии может находиться большое число альтернатив-"потомков", а у критериев-родителей" с низким приоритетом — значительно меньшее число альтернатив-"потомков", чем в первом случае. Поэтому в этой ситуации желательно повышение приоритетов альтернатив в большой группе, поскольку, если альтернатив много, каждая из них получит меньший составной приоритет, чем каждая альтернатива, входящая в меньшую группу с низким приоритетом критерия.

На практике возможны также ситуации, прямо противоположные выше охарактеризованной, когда требуется повысить приоритет так называемых редких альтернатив-"потомков", образующих относительно критериев-"родителей" маленькие группы. В этом случае структурная матрица [L] принимает следующий вид:

Процедура 6. Определяется вектор приоритетов альтернатив W относительно критериев. Данная процедура реализуется последовательным перемножением слева направо следующих матриц и векторов:

а) для случая, когда экспертные оценки в матрице [А] ненормированы:

W=[A] [S][L] [B]; (2.7)

б) для случая, когда экспертные оценки в матрице [А] нормированы:

W=[A] [L] [B]. (2.8)

В выражениях (2.7) и (2.8) диагональная матрица [В] предназначена для окончательного нормирования значений вектора приоритетов альтернатив. Эта матрица имеет следующий вид:

где х_i — значение ненормированного вектора приоритетов альтернатив, полученное после последовательного перемножения слева направо матриц [A], [S], [L] и вектора ;

r — число альтернатив.

Рассмотрим пример вычисления вектора приоритета альтернатив.

Допустим, имеется иерархическая система (рис. 2.8), включающая корневую вершину — фокус (Ф), два критерия К₁ и К₂ и пять альтернатив A₁, ... ,А₅. При этом по критерию К₁ оцениваются все пять альтернатив, а по критерию К₂ — две альтернативы: А₄ и А₅.

Предположим, что при попарном сравнении альтернатив и критериев получены матрицы, отображающие равную предпочтительность сравниваемых объектов.

Матрицы предпочтений альтернатив относительно критериев K₁ и K₂ соответственно примут вид:

Построим матрицу предпочтений критериев относительно фокуса (Ф):

Правые собственные векторы для приведенных матриц имеют следующий вид:

= {0,2 0,2 0,2 0,2 0,2}^T — приоритет альтернатив по критерию K₁;

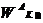= {0,5 0,5}^T — приоритет альтернатив по критерию К₂;

= {0,5 0,5}^T— приоритет критериев относительно фокуса Ф.

Поскольку векторы приоритетов альтернатив относительно критериев K₁ и К₂ нормированы, результирующий вектор рассчитывается по формуле (2.8).

При этом матрицы [А] и [L] и вектор с учетом ранее выполненных расчетов имеют следующий вид:

Производя последовательные перемножения матриц и вектора слева направо, получим следующие результаты:

Следует отметить, что при неучете структурного критерия L результирующий вектор приоритетов альтернатив имеет следующий вид:

W'=[A] = {0,1 0,1 0,1 0,35 0,35}^T.

Из сравнительного анализа двух результирующих векторов W и W' видно, что в первом случае каждая из альтернатив A₄, и A₅, (значение 0,286 в векторе) в два раза весомее любой из альтернатив А₁, A₂ или А₃, (значение 0,143 в векторе), а во втором случае различие между теми же альтернативами большее и равно 3,5 (значение 0,35 против 0,1) для альтернатив в векторе приоритетов W'.

Существуют иерархии (рис. 2.9), у которых, в отличие от ранее рассмотренных (приведенной, например, на рис. 2.8), альтернативы сгруппированы в подмножества {А₁, А₂, ..., А_m}, {А'₁, А'₂, ..., А'_s}, {А"₁, А"₂, ... , A"_l}, а элементы каждого из таких подмножеств связаны, в свою очередь, с определенными группами критериев {K₁₁, K₁₂,...,K₁_m}, {K₂₁, K₂₂,...,K₂_n}, {K_n₁, K_n₂,…,K_np}.

В этом случае перевернутое иерархическое дерево состоит из ряда самостоятельных иерархических ветвей.

Рассмотрим особенности алгоритма для определения векторов приоритетов альтернатив на иерархиях, состоящих из нескольких ветвей. Для лучшего понимания сущности алгоритма проиллюстрируем его на примере конкретной иерархии (см. рис. 2.9).

Алгоритм для иерархии с несколькими ветвями

Шаг 1. Вычисляются векторы приоритетов альтернатив относительно критериев К_ij:

Шаг 2. Строятся r матриц [А_i], у которых наименованиями строк являются альтернативы, а наименованиями столбцов — критерии К_ij . При этом если альтернатива А_i не связана с критерием K_ij , то в матрице [А_i] на пересечении соответствующих строки и столбца проставляется нуль.

Шаг 3. Вычисляются r векторов приоритетов альтернатив W^A_i(i = 1,r) относительно критериев К_i по выражениям:

где [S_i] — матрица для нормирования матрицы [А_i];

[L_i] — структурная матрица для изменения веса альтернатив пропорционально отношению R/N (R — число альтернатив, находящихся под критерием К_ij , N — суммарное число альтернатив);

— вектор приоритетов критериев К_ij относительно критериев К_i;

[B_i] — диагональная матрица для получения нормированного вектора W^A_i, определяемая по выражению (2.9).

Ш а г 4. Вычисляется вектор приоритетов критериев относительно фокуса иерархии К₀.

Шаг 5. Строится результирующая матрица [A₀], у которой наименованиями строк являются все рассматриваемые альтернативы ({А_i}, i = 1,т, {А'_i}, i = 1,s, {А"_i}, i = 1,t), а наименованиями столбцов — критерии К_i. При этом результирующая матрица [Ао]имеет следующий вид:

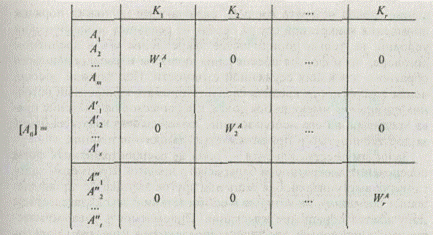
Шаг 6. Определяется результирующий нормированный вектор приоритетов W₀^A всех рассматриваемых альтернатив относительно фокуса иерархии К₀ на основании известного выражения:

W₀^A= [А₀] [S₀] [L₀] [В₀] .

Конец алгоритма.

Дата добавления: 2018-04-15; просмотров: 530; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Мы поможем в написании ваших работ!