Задания к практической работе
Практическая работа №7. Изучение способов нахождения первообразной и методов вычисления определенного интеграла.
Цель занятия:Усовершенствовать навыки нахождения неопределенных и определенных интегралов
Краткие теоретические сведения
Для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Первообразная и неопределенный интеграл.
Функция F(x) называется первообразной функции f(x), если
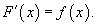
Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как
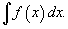
Таким образом, если F - некоторая частная первообразная, то справедливо выражение
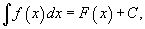
где С - произвольная постоянная.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,
а, k, C - постоянные величины.
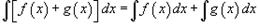
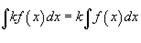
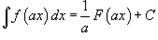
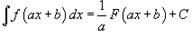
Непосредственное интегрирование– интегрирование с использованием таблицы неопределенных интегралов, основных свойств и тождественных преобразований подынтегральной функции
Пример 1. Сначала приведем полное решение:
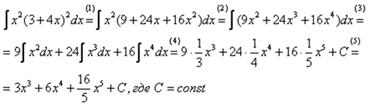
(1) Используем формулу квадрата суммы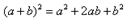 
, избавляясь от степени.
(2) Вносим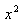 
в скобку, избавляясь от произведения.
(3) Используем свойства линейности интеграла (оба правила сразу).
(4) Превращаем интегралы по табличной формуле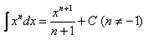 
.
(5) Упрощаем ответ. Здесь следует обратить внимание на обыкновенную неправильную дробь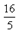 
– она несократима и в ответ входит именно в таком виде.
|
|
|
Пример 2. Найти неопределенный интеграл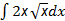 
.
Используя свойство неопределенного интеграла, вынесем за знак интеграла постоянную 2. Затем, выполняя элементарные математические преобразования, приведем подынтегральную функцию к степенному виду:
.
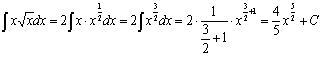Пример 3.
.
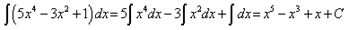Пример 4.
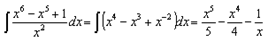
Метод замены переменной.
Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением
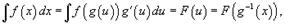
где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой.
Важно иметь ввиду, что дифференциалdx должен быть заменен на дифференциал новой переменной du.
Пример 1.
Вычислить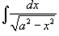 
.
Решение.
Сделаем замену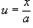 
. Тогда 
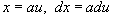. Следовательно, интеграл принимает вид
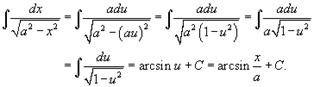
Пример 2.
Вычислить интеграл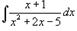 
.
Решение.
Применяем подстановку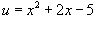 
. Тогда 
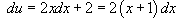или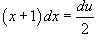 
.
С использованием данной подстановки интеграл легко вычисляется:
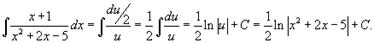
Пример 3.
Найти интеграл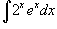 
.
Решение.
Перепишем интеграл в виде
|
|
|
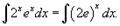
Обозначая 2e = a (это не замена переменной - аргументом по-прежнему остается x), получаем табличный интеграл
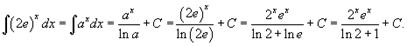
Пример 4.
Вычислить интеграл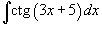 
.
Решение.
Запишем интеграл как
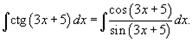
Используя замену
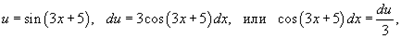
получаем ответ
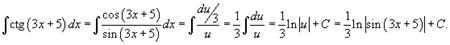
Пример 5.
Вычислить интеграл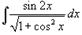 
.
Решение.
Сделаем следующую подстановку:
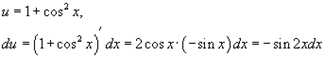
Следовательно,
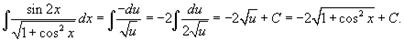
Задания к практической работе.
Дата добавления: 2018-04-04; просмотров: 1167; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!