П.3.Простейшая модификация метода Эйлера – метод Рунге-Кутта 2-го порядка
Заменим приращение функции на первом шаге 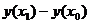 не на
не на 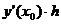 , как делали в методе Эйлера, а на более точное значение - на значение производной в середине интервала
, как делали в методе Эйлера, а на более точное значение - на значение производной в середине интервала 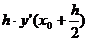 . А для того, чтобы найти
. А для того, чтобы найти 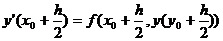 .
.
Заменим 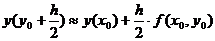
Окончательно получаем следующую формулу:
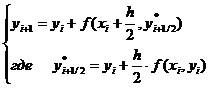
(6.3) Формула Рунге-Кутта 2го порядка с усреднением по
времени.
Метод Рунге-Кутта 2го порядка с усреднением по производной.
Заменим приращение:
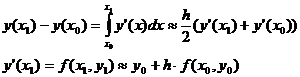
Окончательно получим следующую формулу:
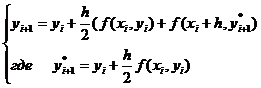
(6.4) Метод Рунге-Кутта 2го порядка с
усреднением по производной.
Локальная погрешность методов (6.3) и (6.4) 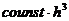
П.4. Сведение дифференциальных уравнений высших порядков к системе дифференциальных уравнений и её решение.
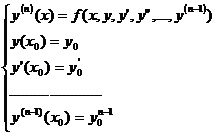 Рассмотрим дифференциальное уравнение nого порядка, разрешенное относительно старшей производной и Задачу Коши для данного уравнения:
Рассмотрим дифференциальное уравнение nого порядка, разрешенное относительно старшей производной и Задачу Коши для данного уравнения:
- ДУ
 |
Задача
Коши
(6.5) - начальные условия.
|
|
|
Чтобы свести З.К.(6.5) для ДУ nого порядка к СДУ 1ого порядка, поступаем следующим образом:
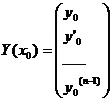
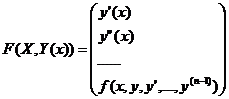 введём вектор-функцию
введём вектор-функцию 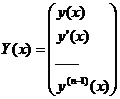 , тогда З.К, (6.5)для ДУ nого порядка сводится к СДУ 1ого порядка:
, тогда З.К, (6.5)для ДУ nого порядка сводится к СДУ 1ого порядка:
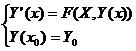 (6.6)
(6.6)
где ;
Итак, вместо З.К. (6.5) для ДУ nого порядка мы получили З.К. (6.6) для СДУ 1ого порядка, а её мы можем решить любым известным нам методом (Эйлера, Рунге-Кутта,…) с заменой в этих формулах скалярных величин y,f на векторные Y,F.
Пример сведения ДУ nого порядка к СДУ 1ого порядка и нахождение решения по методу Эйлера:
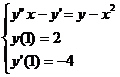
Имеем ДУ 2го порядка, сводим к СДУ 1го порядка для 2х уравнений:
Вводим 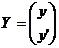
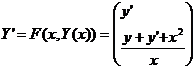
фиксируем шаг: h=0,1
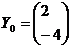
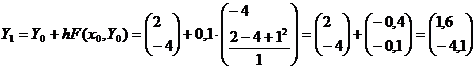
Аналогичным образом находим 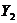
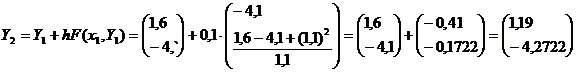
Метод Рунге-Кутта 4го порядка.
Наиболее применяемым методом решения ДУ и СДУ является метод Рунге-Кутта 4го порядка.
Формулы метода Рунге-Кутта 4го порядка:
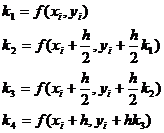 (6.7)
(6.7)
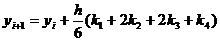
в векторной форме данной формулы, величины y, f, k заменяют на Y, F, K.
П.5. Локальные и глобальные погрешности одношаговых методов решения ДУ
(метода Эйлера и методов Рунге-Кутта 2го, 4го порядка).
|
|
|
Теорема 6.1:
Если локальная погрешность метода 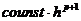 , то глобальная
, то глобальная 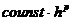 .
.
Комментарии:
как и при численном интегрировании, при переходе от локальной погрешности к глобальной, точность метода уменьшается на порядок. (6.8):
| Методы | Локальная | Глобальная |
| Эйлер | const*h2 | const*h |
| Р.–К. 2го порядка по времени | const*h3 | const*h2 |
| Р.–К. 2го порядка по производной | const*h3 | const*h2 |
| Р.–К. 4го порядка | const*h5 | const*h4 |
Как и при численном интегрировании, порядок метода – степень h в глобальной погрешности.
П.6. Многошаговые методы решения ДУ и СДУ.
Все рассмотренные ранее методы – одношаговые, т.к. для нахождения 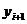 мы использовали только лишь значения
мы использовали только лишь значения  с предыдущего шага. В многошаговых методах для нахождения
с предыдущего шага. В многошаговых методах для нахождения 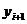 используется не только лишь одно
используется не только лишь одно  , но и предыдущие значения.
, но и предыдущие значения.
В k-шаговом методе используются значения с k предыдущих шагов.
Многошаговые методы, как правило, дают лучший результат, чем одношаговые, в силу того, что более устойчивы к вычислительным погрешностям. Многошаговых методов много, самый распространенный среди них – метод Милна.
Формулы метода Милна:
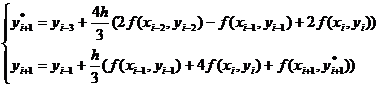 (6.9)
(6.9)
Метод Милна – 4х шаговый (т.к. использует 4 предыдущих значения) и имеет 4-ый порядок точности. Перед применением метода Милна нам надо знать 4y, следовательно, необходимо сделать хотя бы 3 шага каким-нибудь одношаговым методом.
|
|
|
П.7. Оценка погрешности решения ДУ и СДУ методом двойного пересчета. Коррекция решения.
Используя такую же идею, как и в численном интегрировании, находим решение ДУ на [a,b] дважды с шагом h и с шагом h/2. Получим следующую картину:



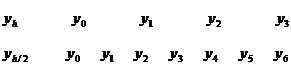
Сравниваем попарно, если расхождение между 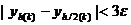 для метода 2го порядка,
для метода 2го порядка, 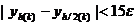 для метода 4го порядка, то в качестве точного решения берём
для метода 4го порядка, то в качестве точного решения берём 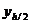 . Если же точность не достигнута, то шаг h уменьшаем вдвое и т.д., пока она не будет достигнута.
. Если же точность не достигнута, то шаг h уменьшаем вдвое и т.д., пока она не будет достигнута.
Метод двойного пересчёта при решении ДУ и СДУ практически единственный имеет возможность для оценки погрешностей, так как иные формулы очень сложны и требуют оценок различных производных.
Как и при ЧИ, при решении ДУ и СДУ после 2го пересчёта в качестве точного решения выгодно брать не 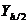 , а
, а 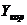 .
.
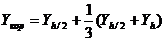 - для второго порядка
- для второго порядка
Метод двойного пересчёта применим не только лишь при ЧИ, при решении ДУ и СДУ, но и при решении других численных методов.
П.7. Краевые задачи для дифференциальных уравнений.
Выше рассматривалось решение ДУ и СДУ с начальными условиями, заданными в одной точке, так называемую задачу Коши, но для ДУ высших порядков часто бывает необходимо решить не з. Коши, а так называемую краевую задачу, т.е. начальные условия, которые заданы в разных точках.
|
|
|
Рассмотрим простейшую краевую задачу для ДУ 2го порядка:
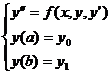 (6.10)
(6.10)
А мы умеем решать:
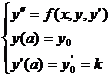 (6.11),
(6.11),
В (6.11) нам известно 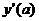 , поэтому для решения задачи (6.10) мы будем подбирать
, поэтому для решения задачи (6.10) мы будем подбирать 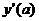 в (6.11), с тем, чтобы у(b) = у1
в (6.11), с тем, чтобы у(b) = у1
Метод стрельб
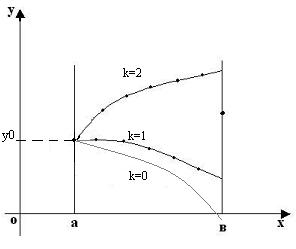
После пристрелки и определения интервала [a,b],
где идёт смена знака, запускаем МПД или МХ.
На практике это выглядит так, как будто мы
решаем уравнение 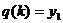 , где
, где 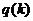 возвращает
возвращает
решение задачи Коши (6.11) в точке b при
заданном k.
Дата добавления: 2018-04-05; просмотров: 515; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
