П.6. Численное интегрирование

Общая идея, решение.

Постановка задачи: в узлах заданы значения функции = f( ) Необходимо найти значение для любых a,b.

Основная идея численного интегрирования: заменить функцию f(x) на интерполирующую ее функцию, которую мы и будем интегрировать.

, где не зависит от исходной функции f, а зависит от узлов интерполяции .

Вычислим :

Замечания:

Замена на 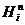была сделана с той целью, чтобы коэффициенты Ч.И. не зависели от h, а зависели от n и i.

Частные случаи, формулы Ньютона - Котеса.

Итак, формула Ч.И. принимает следующий вид:

(5.11б)

где вычисляется по формуле (5.11а).

Выпишем частные случаи (5.11а):

n=1

Таким образом, при n=1, формула Ньютона - Котеса следующий вид:

(5.12) – формула трапеций Ч.И. (выражение из правой части площадь трапеции):

Вычислим коэффициенты Н.-К. n=2:

Итак, при n=2, формула Ч.И. принимает следующий вид (формула Симпсона):

Аналогичным образом вычисляем коэффициенты при большем n.

Таблица коэффициентов Ньютона - Котеса:

_i ⁿ	1	2	3	4	5	6	7	8
H₀	½	1/6	1/8	7/90	19/288	41/840	751/17280	989/28350
H₁	½	2/3	3/8	32/90	75/288	216/840	3577/17280	5888/28350
H₂		1/6	3/8	12/90	60/288	27/840	1323/17280	-928/28350
H₃			1/8	32/90	50/288	272/840	2989/17280	10496/28350
H₄				7/90	75/288	27/840	2989/17280	*/28350
H₅					19/288	216/840	1323/17280	10496/28350
H₆						41/840	3577/17280	-928/28350
H₇							751/17280	*5888/28350
H₈								989/28350

Погрешности формул численного интегрирования.

При численном интегрировании возникают два типа погрешностей: и

Погрешность усечения возникает из-за замены функции f(x) на интерполирующий ее многочлен. Погрешность округления возникает из-за того, что значение функции y_i в узлах интерполяции известно не точно, а приближенно, с некоторой погрешностью η.

Теорема 5.2:

(с учётом знака) для формулы трапеции (5.12)

(5.15)

Комментарии: если f”>0, то <0 ( )

Теорема 5.3:

(с учётом знака) для формулы Симпсона:

(5.16)

Замечания:

Из (5.15) видно – формула трапеций выдаёт правильный результат ( =0), если f – многочлен первой степени (т.к. f”(x)=0). Этого следовало ожидать, т.к. при выведении формулы трапеции мы заменяли f(x) на И.М. её первой степени, который совпадает с f(x).

По этой причине логично ожидать, что для формулы Симпсона будет нулевой, если f – многочлен второй степени (т.к. в формуле Симпсона происходит интерполяция по трём точкам). Как мы видим из (5.16) формула Симпсона будет верна не только для многочлена третей степени, т.к. f””(x)=0.

Общие формулы трапеции и Симпсона численного интегрирования.

Если требуется найти на большом промежутке, то мы разбиваем этот интервал на множество меньших интервалов, на каждом из которых применяем соответствующую формулу Ньютона – Котеса (трапеции или Симпсона).

Общая формула трапеций.

(5.17)

Общая формула Симпсона.

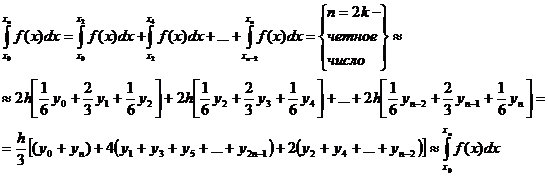Т.к. в формуле Симпсона участвует интеграл от до , то, при разбиении исходного участка, мы группируем интервалы попарно и поэтому n=2k (общее количество участков должно быть чётное).

(5.18)

Погрешности общих формул трапеции и Симпсона.

Погрешности усечения общей формулы трапеции и общей формулы Симпсона состоят из суммы погрешностей усечения формулы трапеции и формулы Симпсона на каждом интервале.

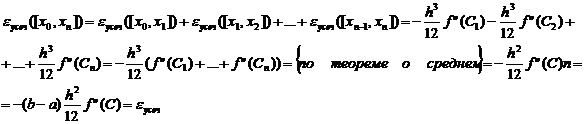
для общей формулы трапеции (5.17):