Чтобы чётко читать чертёж, применяют понятие «разрезы»
Разрезом называют изображение изделия, мысленно рассечённого одной или несколькими секущими плоскостями, при этом ту часть изделия, которая расположена между наблюдателем и секущей плоскостью, удаляют.
На разрезе показывается то, что получается в секущей плоскости и что расположено за ней. Построенный разрез на одном из видов не влияет на другие виды.
Рис.3.3
Разрезы на чертежах обозначаются (рис.3.3):
- двумя штрихами ГОСТ 2.303 – 68 «Линии чертежа» (толщина в два раза толще, длина 8 – 20 мм), проведёнными за контурной линией;
- стрелками (размер в два раза больше размерных), показывающими направление взгляда;
- буквенное обозначение, например, А – А, Б – Б и т.д.
Если направление секущей плоскости совпадает с осью симметрии проекции, то на чертеже разрез не обозначается (рис.3.4).
По расположению секущих плоскостей разрезы делятся на:
горизонтальные (рис.3.3) и вертикальные.
Вертикальные разрезы по расположению секущей плоскости к плоскостям проекций делятся на:
фронтальные и профильные. Следовательно, фронтальный разрез расположен на главном виде, горизонтальный разрез – на виде сверху, профильный разрез – на виде слева.
Если вид, разрез или сечение представляют симметричную фигуру, то совмещают половину вида и половину соответствующего разреза, разделяя их осью симметрии (рис.3.4) или волнистой линией, если с осевой линией совпало ребро (рис.3.5).
|
|
|
Разрезы выполняются только справа или снизу от оси симметрии.
Рис.3.4 Рис.3.5
Для выполнения сечения применяются те же элементы, что и для
разреза.
Разница: в сечении показывают только то, что попадает в секущую плоскость, а что расположено за ней – не показывают (рис.3.6).
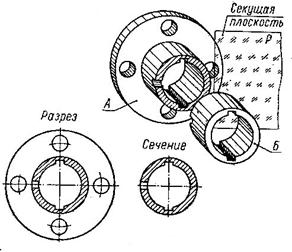
Рис.3.6.
Аксонометрические проекции
Чертёж, выполненный в прямоугольных проекциях, является основным видом изображения, которым пользуются на практике. Для облегчения пространственного представления об изделии иногда применяются аксонометрические проекции (аксонометрия – измерение по осям). Аксонометрические проекции передают одним изображением форму изделия в трёх измерениях (дли, ширина и высота, т.е. по трём осям). Вид изделия приближается в этом случае к тому, который воспринимает наше зрение при рассматривании его в натуре.
Аксонометрическая проекция, применяемая как технический рисунок, нагляднее ортогонального (плоского) изображения, но обладает некоторыми недостатками.
|
|
|
Главными из них являются некоторые искажения форм и размеров изделия. Эти искажения зависят от вида аксонометрии.
Если изделие с осями прямоугольных координат расположить перед плоскостью проекций и проецировать параллельными лучами на одну плоскость (картинную плоскость), то получают аксонометрическую проекцию.
ГОСТ 2.317 -69 устанавливает следующие виды аксонометрических проекций:
- прямоугольные – проецирующие лучи перпендикулярны картинной плоскости;
- косоугольные – проецирующие лучи наклонны картинной плоскости.
Прямоугольные аксонометрические проекции делятся на:
- прямоугольную изометрию, которая имеет единый масштаб для трёх осей (рис.3.7- а); дано построение координатных осей с помощью окружности произвольного радиуса;
- прямоугольную диметрию, имеющую по двум осям одинаковые масштабы, а для третьей оси - другой масштаб (рис.3.7- б);
- триметрическую проекцию, имеющую разные масштабы по трём
осям.
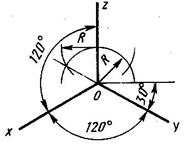
а) б)
Рис.3.7
Для всех видов аксонометрических проекций при построении изделия некоторые положения в построении чертежа будут одинаковыми, а именно:
|
|
|
- любому чертежу в аксонометрических проекциях должен предшествовать чертёж, выполненный в ортогональных проекциях (комплексный чертёж – рис.3.8 а);
- ось Z проецируется всегда вертикально;
- все измерения делаются только по осям или параллельно осям;
- все прямые линии, параллельные между собой или параллельные осям симметрии на ортогональном чертеже, остаются параллельными в аксонометрии.
На рис.3.8 показано построение прямоугольной изометрии с учётом положений указанных выше. В данном случае построение аксонометрии показано с передней грани и т.д. по осям, откладывая соответствующие размеры без искажения с комплексного чертежа.
Прямоугольная изометрия – Аксонометрическая проекция, имеющая одинаковые коэффициенты искажения по осям - 0,82.
Для упрощения выполнения чертежей коэффициент искажения по осям принимают равным 1. Получается увеличенное изображение, причём увеличение происходит в 1: 0,82 = 1,22 – коэффициент приведения.
Окружности проецируются на аксонометрическую плоскость в виде эллипсов – большая ось 1,22D, а малая ось– 0,71D.
|
|
|
Пример изометрической проекции детали дан на рис.3.9- а и проекции куба с вписанными в его грани окружностями в виде эллипсов – на рис.3.9 б.
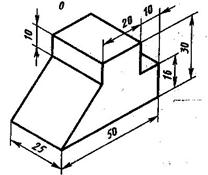
Рис.3.8
а б
Рис.3.9
Прямоугольная диметрия - аксонометрическая проекция, имеющая коэффициент искажения по оси Y равен 0,47 , а по осям Х и Z – 0,94.
Для упрощения выполнения чертежей коэффициент искажения по осям принимают - по оси Y – 0,5, а по осям Х и Z - 1. Получается увеличенное изображение, причём увеличение происходит в 1:0,94 = 1,06 – коэффициент приведения.
Окружности проецируются на аксонометрическую плоскость также в виде эллипсов – большая ось 1,06D (D - без упрощения), а малая ось – 0,35D (0,33D - без упрощения).
Пример диметрической проекции детали дан на рис.3.10 - а и проекции окружности в виде эллипсов – на рис.3.10- б.
Прямоугольная диметрия часто применяется для изделий, имеющих призматические поверхности.
а)
Рис.3.10 б)
Построение плоских фигур
На рис.3.11- а показано построение шестиугольника (прямоугольная изометрия) с размерами и дано изображение его в трёх плоскостях. где стороны параллельны соответствующим координатным осям.
а) б)
Рис.3.11
На рис.3.11 – б дано построение квадрата (прямоугольная диметрия) с размерами и дано изображение его в трёх плоскостях, где стороны параллельны соответствующим координатным осям. По рисунку видно, что по оси Y размер стороны квадрата уменьшается в два раза, а по другим осям без изменения.
Дата добавления: 2018-04-05; просмотров: 305; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!