Студенты должны выполнять самостоятельно

Сопряжения.

Сопряжениемв инженерной графике называется плавный переход от одной линии к другой линии.

Для построения сопряжения надо найти центры, из которых проводят дуги, т.е. центры сопряжений. Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжения. При построении контура изображения сопрягающиеся линии нужно доводить до этих точек. Следовательно, для любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точки сопряжения.

Сопряжение двух прямых линий, образующих угол:

Рис.2.15 Рис.2.16

Для построения сопряжения двух прямых линий (рис.2.15), образующих угол, необходимо провести параллельные прямые на расстоянии равном радиусу сопряжения. Пересечение этих параллельных прямых даёт точку О – центр сопряжения. Из этой точки О опускаем перпендикуляры на стороны данного угла – получаем точки сопряжения. Соединяем полученные две точки данным радиусом сопряжения R.

Сопряжение окружности с прямой линией (рис.2.16).

Для построения сопряжения необходимо от данной прямой АВ провести параллельную прямую линию на расстоянии равном радиусу сопряжения R_а и из заданного центра О провести дугу суммой радиусов R + R_а. Пересечение параллельной прямой и дуги суммой радиусов даёт точку О₁ – центр сопряжения. Соединяем точки О и О₁ - получили первую точку сопряжения m. Из точки О₁ опускаем перпендикуляр на заданную прямую АВ – получили вторую точку сопряжения n. Соединяем полученные точки сопряжения заданной дугой сопряжения R_а.

Внешнее касание двух дуг (рис.2.17).

Для построения внешней касательной (внешнее касание двух дуг –рис.2.17) к двум окружностям необходимо провести вспомогательную окружность из центра О радиусом равным разности заданных дуг окружностей. Делим расстояние между окружностями пополам и полученная дуга, проведённая из середины пересекает вспомогательную окружность в точке а. Соединяем точки О и а и продолжаем до пересечения с данной дугой – получили точку m, точку сопряжения. Из точки О₁ проводим прямую параллельную прямой Оm – получили точку р, вторую точку сопряжения. Соединяем полученные точки сопряжения прямой линией - получили внешнюю касательную прямую к данным окружностям.

а) б)

Рис.2.17 Рис.2.18

Сопряжение двух дуг окружностей (рис.2.18).

Построение сопряжений двух дуг окружностей подробно показано на рис.2.18. При внешнем касании сопрягающая дуга R₃ касается заданных окружностей внешней стороной. Для нахождения центра радиуса сопряжения проводим вспомогательные окружности из заданных центров суммой радиусов.

Точки сопряжения определяются соединением заданных центров с построенным центром сопряжения О₃. Такие же построения выполняются при внутреннем касании, что видно по рис.2.18 –б.

Пример детали, контуры которой вычерчивают с помощью сопряжений, показан на рис. 2.19

Вычерчивание выполняется в следующей последовательности:

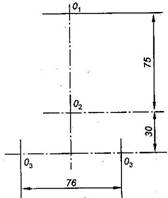
1.Проводятся оси симметрии детали и все центровые линии, определяющие центры О₁, О₂, О₃ по заданным размерам (рис.2.19- а);

2.Из центров проводятся окружности заданных радиусов R₁= 25мм, R₂ = 30мм, R₃ = 20мм и D₁ = 25мм, D₂ =30мм, D₃ = 26мм ; также проводятся две параллельные линии на расстоянии S= 16мм (рис.2.19 –б);.

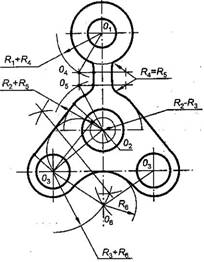
3. Применяя построение сопряжений окружности с прямой линией (рис.2.16), находятся центры дуг сопряжений О₄ и О₅ ( рис.2.19 –в);

4.Применяя построение сопряжений двух дуг окружностей (рис.2.18 а), находят центр сопряжения О₆ 9рис.2.19 в);

5.Применяя построение внешней касательной к дугам окружностей (рис.2.17), проводят прямую линию (рис.2.19 в);

6.Обводится контур детали в последовательности: дуги сопряжений, основные окружности и дуги, прямые линии;

7. С выполненного чертежа убираются линии построения (иногда оставляют) и наносятся размеры по ГОСТ 2.307-68.

а) б)

в) г)

Рис.2.19

Лекальные кривые.

Эти кривые (эллипс, парабола, гипербола, эвольвента, спираль Архимеда и др.) строятся путём нахождения отдельных точек и вычерчиваются с помощью специальных линеек - лекал.

До обводки кривой по лекалу рекомендуется соединить полученные точки при построении тонкой линией от руки на глаз, стараясь придать этой кривой лини и возможно более плавные очертания, и лишь после этого подобрать участок линейки–лекало, соответствующей кривизне того или другого участка, соединяя не менее трёх точек одновременно.

а) б) в)

г) д)

ж)

е)

з)

Рис.2.20

Эллипс (рис.2.20 а).

На рисунке показано построение эллипса по двум заданным осям АВ и СD. Для этого по размерам данных осей проводим две окружности: большую и малую. Большую окружность делим на равные части, например 12 частей. Точки деления соединяем с центром О. Полученные радиальные прямые линии пересекают малую окружность в точках: 1_1, 2₁, …. и т.д.

Из точек деления большой окружности проводим прямые, параллельные малой оси эллипса, а из точек деления малой окружности – прямые, параллельные большой оси эллипса. Пересекаясь, эти линии дают точки, принадлежащие эллипсу.

Парабола (рис.2.20 б).

На рисунке показано построение параболы по фокальному параметру р (директрисе и фокусу F). Проводим две взаимно перпендикулярные прямые - директрису СD и ось параболы ВЕ, на которой откладываем отрезок ВF, равный заданному параметру р. Получаем фокус параболы - F. Вершина А лежит посередине отрезка ВF. На оси ВЕ от вершины А намечаем произвольные точки 1, 2, 3, .. и т.д. и через них проводим прямые, перпендикулярные к оси параболы. Затем радиусом R, равным расстояниям В1, В2, В3, и т.д. делаем засечки (дуги) на параллельных прямых линиях, проведённых через точки деления. На пересечении получаем точки, принадлежащие параболе.

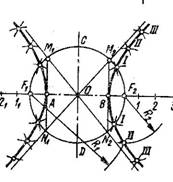
Гипербола (рис.2.20. в).

На рисунке показано построение гиперболы по фокусному расстоянию и расстоянию между вершинами АВ. Проводим две взаимно перпендикулярные прямые АВ и СD – оси гиперболы, где АВ - действительная ось, а СD – мнимая ось. Фокусы гиперболы находятся на равных расстояниях от точки О – центра гиперболы, а вершины А и В на равных расстояниях от фокусов.

Далее строим асимптоты гиперболы – прямые, проходящие через центр, к которым неограниченно приближаются ветви гиперболы по мере удаления их в бесконечность. Для построения асимптот из центра О радиусом R = ОF₁ = ОF₂ проводят вспомогательную окружность. Из вершин А и В восставляем перпендикуляры к действительной оси АВ до пересечения со вспомогательной окружностью - получили точки М₁ и М₂ слева и точки N₁ и N₂ справа от вертикальной оси гиперболы. Проводим прямые линии М₁N₂ и М₂N₁ , которые будут асимптотами гиперболы.

Для построения правой ветви гиперболы на прямой линии АВ правее фокуса F₂ намечаем произвольные точки 1, 2, 3, ..и т.д. Затем радиусом R₁, равным расстояниям А1, А2, А3, и т.д., делаем засечки дугой из фокуса F₁ около асимптот симметрично относительно действительной оси АВ. Из фокуса F₂ делаем засечки дугой радиусом R₂, равным расстояниям В1, В2, В3, и т.д. На рисунке показано проведение этих радиусов для одной из точек гиперболы. Пересечение двух засечек (дуг) дают точки гиперболы с правой стороны. Такие же построения выполняем для левой ветви гиперболы.

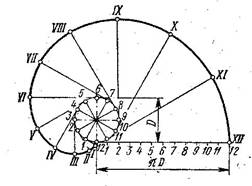
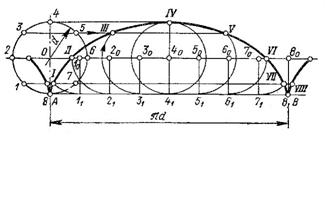
Эвольвента (рис.2.20. г).

На рисунке показано построение эвольвенты по окружности заданного диаметра. Делим заданную окружность на равные части, например 12. Проводим радиальные прямые и касательные к окружности в точках деления, направленные в одну сторону. На касательной, проведённой через последнюю точку 12, откладываем отрезок, равный длине окружности – πD. Делим данный отрезок на такое же число частей, как и окружность - 12. Затем на каждой касательной откладываем отрезки, равные длинам разделённого отрезка: на первой касательной - отрезок О1, на второй - отрезок О2, на третьей - отрезок О3 и т.д. Итак, на последней касательной будет весь отрезок - πD.

Полученные точки на касательных будут принадлежать эвольвенте.

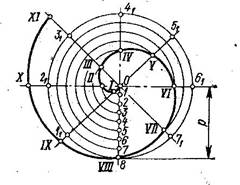
Спираль Архимеда (рис.2.20 д).

На рисунке показано построение спирали Архимеда по заданной окружности, в которую требуется вписать эту кривую. Делим окружность точками 1₁, 2₁, 3₁, 4₁, и т.д. и радиус - 1, 2, 3, 4, и т.д. на равное число частей, например 8. Через точки деления окружности проводим радиальные прямые линии. Из центра О проводим дуги из точек деления радиуса до пересечения с одноимёнными точками 1 – 1_1,, 2 – 2₁, 3 - 3₁, 4 – 4₁, и т. д.

Полученные точки являются точками данной кривой.

Кардиоида (рис.2.20 е).

На рисунке показано построение кардиоиды по окружности заданного диаметра. На окружности берём произвольную точку М и относительно этой точки делим окружность на чётное число частей, например, 8. Через точки деления окружности и точку М проводим секущие (прямые линии) по обе стороны от точек деления окружности. На этих секущих откладываем отрезки относительно точек деления окружности, равные диаметру окружности. Полученные две симметричные точки на каждой секущей принадлежат данной кривой.

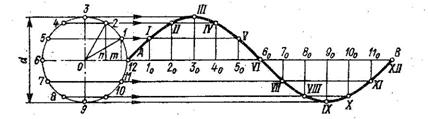
Синусоида (рис.2.20 ж).

На рисунке показано построение синусоиды по окружности заданного диаметра. Делим заданную окружность на равные части, например 12. Проводим прямую линию АВ, равную длине окружности - πD. Делим данный отрезок на такое же число частей. как и окружность - 12. Проводя через точки деления окружности горизонтальные прямые (параллельно прямой АВ), а через точки деления прямой линии АВ - вертикальные, находим в пересечении одноимённых точек точки, принадлежащие синусоиде.

Циклоида (рис.2.20 з).

На рисунке показано построение циклоиды по окружности заданного диаметра. Делим заданную окружность на равные части, например восемь. По направляющей прямой АВ от точки А откладываем отрезок, равный длине окружности πD. Этот отрезок делим на такое же число частей, т.е. восемь- 1₁, 2₁, 3₁, 4₁ и т.д.

Проводим прямую линию параллельно АВ из центра заданной окружности, а из точек деления отрезка восставляем перпендикуляры до пересечения с этой прямой – получили точки 1₀, 2₀, 3₀, 4₀ и т.д. Из этих точек проводим вспомогательные окружности заданного диаметра или дуги, которые касаются прямой АВ.

Через точки деления заданной окружности проводим прямые линии, параллельные отрезку АВ. Затем находим точку пересечения первой вспомогательной окружности с прямой, проведённой через точку деления 1 окружности. Второй вспомогательной окружности с параллельной прямой, проведённой через точку 2 и т.д. Полученные точки будут принадлежать циклоиде.

Конусность и уклон.

Конусностью называетсяотношение диаметра окружности основания прямого конуса к его высоте, а для усечённого конуса – отношение разности диаметров оснований к его высоте (рис.2.17 а), т.е.

D D - d

К = ---- или К = -------

h h₁

Если по чертежу требуется построить заданную конусность, например,

К = 1 : 5, то по формулам необходимо выполнить следующее:

- для усечённого конуса должны быть размеры D и h₁ ;

- из формулы определяем d = D  К· h₁; подставляем известные размеры;

- чертим по размерам данную деталь, отмеряя D, d, h₁.

а) б)

Рис.2.21

Знак конуса и конусности в виде соотношения следует наносить над осевой линии или полке линии – выноске (рис.2.21 б).

Уклонпрямой характеризует её наклон к другой прямой, обычно горизонтальной и реже вертикальной.

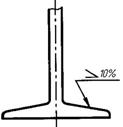
Рис.2.22

Для построения уклона (рис.2.22) необходимо дополнительно построить прямоугольный треугольник со сторонами 100 и 10мм (уклон 10%) и гипотенузу перенести параллельно на ту часть детали, где указан уклон.

2.3. Последовательность выполнения работы:

1.На первом формате А3 оформить внутреннюю рамку и основную надпись. В правой половине формата чертим деталь по индивидуальному заданию (рис.1.1) с построением сопряжений.

Чертёж указанной детали желательно выполнить в масштабе 1:1, соблюдая «заполняемость» рабочего поля около 80%. Допускается применение других масштабов.

Прежде чем начинать чертить, проводим анализ графического состава изображения, чтобы установить, какие геометрические построения необходимо применить. По размерам разделим те линии, которые сразу можно построить с помощью чертёжных инструментов, а другие – для которых нужны построения сопряжений. Вначале проводим те линии, положение которых определено заданными размерами, а затем строим сопряжения, применяя разные случаи построения сопряжений.

Выполнив все построения, делаем обводку данного задания.

2. В левой половине формата А3 чертим лекальную кривую по своему варианту, применяя свой масштаб или оставляя 1:1 по размерам, указанным в задании.

Для вычерчивания лекальной кривой необходимо внимательно разобраться с построением указанной кривой, а затем перенести на формат.

3. Второй формат А3 делим на два формата А4 и каждый формат оформляем внутренней чертёжной рамкой и основной надписью. На одном формате А4 чертим прокатный профиль: двутавр или швеллер.

Для прокатного профиля нужно учесть, что средняя часть по высоте профиля можно изображать с применением линии обрыва, поэтому масштаб можно применять увеличенный. Для этого мысленно вырезаем среднюю часть и сдвигаем верхнюю и нижнюю полки, где больше всего построений с выполнением уклона. Но размер по высоте профиля ставим действительный без обрыва размерной линии.

4. На втором формате А4 чертим деталь с конусностью - валик. При выполнении данного чертежа необходимо научиться применять построение конусности на разных изделиях (деталях).

После выполнения всех четырёх пунктов проверяем оба формата с соблюдением всех ГОСТов ЕСКД 2 класса 3 группы «Общие правила выполнения чертежей».

5.Примеры выполнения работ после индивидуальных заданий на стр. 35 и 36 на рис.2.27 и 2.28

Дата добавления: 2018-04-05; просмотров: 225; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!