Изменение моментов инерции при повороте осей
Пусть известны моменты инерции Jz, Jy и Jzy относительно осей Oyz. Необходимо определить моменты инерции Ju, Jv и Juv относительно осей Ouv, повернутых по отношению к осям Oyz на угол a (рис. 3.6).

Рис 3.6. Изменение моментов инерции при повороте осей
Из геометрических построений следует, что между координатами z, y и u, v существуют следующие соотношения:
| u = z cos a + y sin a; v = y cos a – z sin a. | (3.13) |
Вычислим моменты инерции Ju, Jv и Juv:

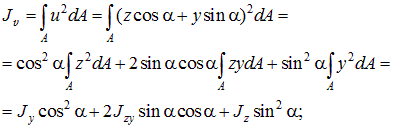
 
| (3.14) |
Используя тригонометрические формулы:
2sin a×cos a = sin 2a,
cos2 a = (1+ cos 2a)/2,
sin2 a = (1– cos 2a)/2,
получаем



| (3.15) |
Сложив первые две формулы (3.14), получим Ju + Jv = Jz + Jy, т.е. при любом повороте взаимно перпендикулярных осей сумма осевых моментов инерции остается величиной постоянной (инвариантом).
Главные оси и главные моменты инерции
Исследуем функцию Ju(a) на экстремум. Для этого приравняем нулю производную Ju(a) по a.
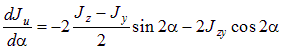
| (3.16) |
Отсюда следует

| (3.17) |
Ту же самую формулу получим, приравнивая нулю центробежный момент инерции
 .
.
Главными осями называют оси, относительно которых осевые моменты инерции принимают экстремальные значения, а центробежный момент инерции равен нулю.
Главных осей инерции можно провести бесчисленное множество, взяв в качестве начала координат любую точку на плоскости. Для решения задач сопротивления материалов нас интересуют только главные центральные оси инерции. Главные центральные оси инерции проходят через центр тяжести сечения.
|
|
|
Формула (3.17) дает два решения, отличающихся на 90°, т.е. позволяет определить два значения угла наклона главных осей инерции относительно первоначальных осей. Относительно какой из осей получается максимальный осевой момент инерции J1= Jmax, а относительно какой – минимальный J2= Jmin, придется решать по смыслу задачи.
Более удобными оказываются другие формулы, которые однозначно определяют положение главных осей 1 и 2 (даются без вывода). При этом положительный угол отсчитывается от оси Оz против часовой стрелки.


| (3.18) |
Используя две первые формулы (3.15) и формулу (3.17), путем несложных преобразований можно избавиться от тригонометрических функций и получить следующее выражение для определения главных моментов инерции.

| (3.19) |
В формуле (3.19) знак «+» соответствует максимальному моменту инерции, а знак «–» минимальному.
Замечание.Если сечение имеет хотя бы одну ось симметрии, то относительно этой оси и любой другой, ей перпендикулярной, центробежный момент инерции равен нулю. В соответствии с определением главных осей инерции можно заключить, что эти оси являются главными осями инерции, т.е. ось симметрии – всегда главная центральная ось.
|
|
|
Для симметричных профилей, представленных в сортаменте, швеллера или двутавра, главными центральными осями инерции будут вертикальная и горизонтальная оси, пересекающиеся на половине высоты профиля.
Дата добавления: 2018-04-05; просмотров: 872; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
