Моменты инерции простых сечений
В данном разделе приводятся формулы для вычисления моментов инерции простейших фигур, из которых могут быть составлены более сложные (составные) сечения.
Прямоугольник.Рассмотрим прямоугольное сечение со сторонами b и h, представленное на рис. 3.7. Центр тяжести прямоугольника С расположен на пересечении диагоналей. Оси Сz и Сy являются главными центральными осями инерции. Так как обе они являются осями симметрии, то Jzy = 0.

Рис 3.7. К выводу моментов инерции прямоугольника
Найдем осевые моменты инерции относительно осей Сz и Сy, подставляя dA=dzdy в формулы (3.3) и производя интегрирование:

| (3.20) |
Аналогично:

| (3.21) |
Так как вертикальная ось является осью симметрии, получаем Jzy=0.
Треугольники.Аналогичным образом можно вычислить моменты инерции треугольников. Выводы этих формул здесь не приводятся.
Произвольный треугольник. Приведем только формулу для вычисления осевого момента инерции относительно центральной оси Сz.

Рис 3.8. К определению момента инерции произвольного треугольника
Основание b и высота h, а, следовательно, и площади трех треугольников будут одинаковыми. Центры тяжести расположены на расстоянии одной трети высоты от основания. Осевые моменты инерции относительно центральной оси z также будут одинаковыми и определяются по формуле

| (3.22) |
Равнобедренный треугольник. Оси Сz и Сy являются главными центральными осями инерции, так как Сy – ось симметрии.
|
|
|

Рис 3.9. К определению момента инерции равнобедренного треугольника
Поэтому центробежный момент инерции относительно этих осей равен нулю, а Jz и Jy будут являться главными моментами инерции.
 ; ;  ; ;  . .
| (3.23) |
Прямоугольный треугольник. Как следует из раздела, в котором рассмотрен произвольный треугольник, для прямоугольного треугольника получим:
 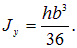
| (3.24) |

Рис 3.10. К определению моментов инерции прямоугольного треугольника
Центробежный момент инерции для треугольника, показанного на рис. 3.10, а, будет равен

| (3.19) |
а для треугольника, изображенного на рис. 3.10, б,

| (3.20) |
Рассуждения по поводу определения знака Jzy аналогичны тем, которые были приведены ранее при обсуждении знака центробежного момента инерции уголка. Центробежный момент инерции Jzy прямоугольного треугольника, расположенного так, как показано на рис. 3.10,а, будет положительным. Если разбить сечение на четыре части и по каждой из них отдельно определить центробежные моменты инерции, то интегралы, вычисленные для частей, расположенных в I и III четвертях будут положительными (произведение zy больше нуля), а для частей во II и IV четвертях будут отрицательными. Однако за счет того, что части в I и III четвертях сами по себе больше и дальше удалены от осей, положительная составляющая окажется больше. На рис. 3.10, б представлено другое положение прямоугольного треугольника относительно осей координат. В этом случае похожие рассуждения приведут к тому, что сумма центробежных моментов инерции по всем четырем частям будет отрицательной.
|
|
|
Круг и кольцо. Получим сначала формулу для вычисления полярного момента инерции круга (рис. 3.11). Площадь малого элемента равна  .
.

| Рис 3.11. К определению моментов инерции круга и кольца |
Произведем интегрирование в полярных координатах:

| (3.21) |
Учитывая равенство Jр = Jz + Jy и очевидное равенство осевых моментов инерции, получаем формулы для определения моментов инерции круга относительно осей, проходящих через его центр
 ; ;  . .
| (3.22) |
Формулы для кольца получим, вычитая из момента инерции внешнего круга момент инерции внутреннего круга радиусом r1 и вводя обозначение k = d1/d:
 ; ;  . .
| (3.23) |
Полукруг.Положение центра тяжести и формулы для определения моментов инерции полукруга (рис. 3.12) приведем без вывода:
|
|
|
  
| (3.24) |

| Рис 3.12. К определению моментов инерции полукруга |
Дата добавления: 2018-04-05; просмотров: 3048; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
