Второй закон термодинамики заключается в том, что все процессы превращения энергии протекают с рассеиванием части энергии в виде тепла

БИЛЕТ-1

1) Кинематика материальной точки. Понятия радиус-вектор, траектория, длина пути, скорость, ускорение. Нормальное и тангенциальное ускорение.

Материальная точка — тело, обладающее массой, размерами которого можно в данной задаче пренебречь.

Радиус-вектор — вектор, соединяющий начало отсчета с положением материальной точки в произвольный момент времени.

Траектория — воображаемая линия, соединяющая положения материальной точки в ближайшие последовательные моменты времени

Длина пути — длина участка траектории, пройденного материальной точкой за данный промежуток времени.

Скорость — векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, в течение которого это перемещение произошло.Единица скорости — метр в секунду (м/с).

Ускорение — векторная физическая величина, равная пределу отношения изменения скорости тела к промежутку времени, в течение которого это изменение произошло.Единица ускорения — метр на секунду в квадрате (м/с²)

Средняя скорость — скалярная величина, равная отношению пройденного пути к промежутку времени, в течение которого этот путь пройден.

Пусть материальная точка совершает движение в выбранной СО. Вектор, проведённый из начального положения точки в конечное называется перемещением ( ). Тогда векторная величина называется средней скоростью перемещения. Длина участка траектории, пройденного точкой за промежуток , называется путём S ( ). Средняя скорость характеризует быстроту и направление движения частиц. Среднюю быстроту движения тела по траектории характеризует средняя путевая скорость 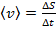. Как быстро и в каком направлении движется тело в данный момент t характеризует мгновенная скорость . Мгновенная путевая скорость 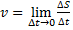. При Модуль мгновенной скорости равен мгновенной путевой скорости Мгновенная скорость всегда направленна по касательной к траектории. Для бесконечно малого перемещения . Для небольших промежутков выполняется приближённо.

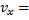
Скорость – векторная величина, значит, её можно записать в виде . С другой стороны . Следовательно, проекция скорости … Величина (модуль) скорости .

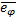Выражение для скорости в полярных координатах ( ): , . Направление задаётся углом или единичным вектором . Радиус-вектор точки , , – единичный вектор, перпендикулярный . .

Пройденный путь частицы от до .

Нормальное и тангенциальное ускорение.

При движении материальной точки её скорость меняется как по величине, так и по направлению. Как быстро это происходит в произвольный момент времени, характеризует векторная величина ускорение. . Проекция вектора ускорения …

Рассмотрим движение частицы, совершаемое в плоскости. Скорость направлена по касательной траектории, поэтому можно записать . Здесь единичный вектор 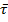задаёт направление касательной, .

Ускорение , направленное по касательной к траектории, определяемое скоростью изменение величины скорости, или модуля, называется тангенциальным ускорением.

– нормальное ускорение (характеризует быстроту изменения направления скорости), - единичный вектор, перпендикулярный и направленный внутрь кривой, R – радиус кривизны линии.

2) Уравнение Ван-дер-Ваальса

Уравнение состояния реального газа (уравнение Ван-дер-Ваальса) для одного моля имеет вид:

где р - давление, оказываемое на стенки сосуда, V_М – объем одного моля газа, а и b - постоянные Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем. Поправка 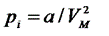– внутреннее давление, обусловленное силами взаимного притяжения между молекулами. Поправка b характеризует ту часть объем, которая недоступна для движения молекул. Она равна учетверенному собственному объему молекул, содержащихся в моле газа:

b= N_A.

Уравнение Ван-дер-Ваальса для произвольной массы газа имеет вид:

Уравнение Ван-дер-Ваальса позволяет построить теоретические изотермы реального газа и сравнить их с изотермами идеального газа и экспериментальными изотермами реального газа.

Уравнение Ван-дер-Ваальса после нескольких преобразований можно записать в виде:

Это уравнение третьей степени относительно V. Кубическое уравнение может иметь либо три вещественных корня, либо один вещественный и два мнимых.

Первому случаю соответствуют изотермы при низких температурах – кривые для Т₁ и Т₂ (рис.9.1.) Второму случаю изотермы при высоких температурах (одно значение объема V отвечает одному значению давления р), то есть любая изотерма начиная от изотермы для Т_к.

Совпадение изотерм идеального и реального газа наблюдается при малых давлениях и больших объемах (так как при этих условиях газ можно считать идеальным). Для семейства изотерм Ван-дер-Ваальса характерно так называемой критической изотермы (при температуре Т_к) имеющий точку перегиба при некотором давлении р_к и объеме V_к; при Т>Т_к все изотермы идут монотонно, при Т <Т_к все изотермы имеют минимум и максимум.

Экспериментальные изотермы, снятые при температурах выше критической, отражают монотонное увеличение давлений газа при уменьшении его объема. При температурах, меньше критической, эксперимент показывает, что изотермы на участке 2,6 имеют «полочку». Часть 6–7 отвечает газообразному состоянию, а часть 1–2 – жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6-2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.

Состояния на участке 3–4–5 не наблюдаются экспериментально; состояния 2–3 и 5–6 могут быть реализованы при особых условиях. Участок 2–3 соответствует т.н. перегретой жидкости. Участок 5-6 – пересыщенному пару (рис.9.2). Эти неустойчивые состояния называются метастабильными. Горизонтальный участок реальной изотермы расположен так, что площади, ограниченные им и теоретической изотерме. В обоих случаях работа должна быть одинакова, следовательно, указанные выше площади должны быть равновелики.

Уравнение Ван-дер-Ваальса описывает не только свойства газов и паров, но и жидкостей. Анализ изотерм реального газа показывает, что превращение реального газа в жидкость возможно только при температурах, меньших критической, и при соответствующих давлениях.

БИЛЕТ-2

Момент силы - произведение прилагаемой силы F на плечо силы L M = F·L

Единицы измерения момента силы:

· СИ - Н·м

С вращателным движением объектов неразрывно связано понятие приложения момента силы.

Наверняка, многие знают жизненную аксиому - чем длиннее рычаг, тем легче сдвинуть груз. Если переложить этот процесс на язык физики, то можно сказать, что применение силы с помощью рычага характеризуется моментом силы.

Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек

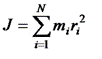(76)

Рис. 26.

К определению момента инерции точки

В случае если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объёмы dv, каждый из которых обладает массой dm. В результате получается следующее выражение:

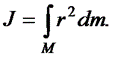(77)

Для однородного по объёму тела плотность ρ постоянна, и записав элементарную массу в виде

dm = ρdv, преобразуем формулу (70) следующим образом:

(78)

Размерность момента инерции – кг*м².

Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.

Момент инерции — это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения. Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.

Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое. Аналогично массе момент инерции является величиной аддитивной.

В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.

Момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:

Момент инерции шара радиуса R:

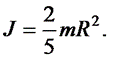
Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:

Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:

Момент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера:

Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.

Рассчитаем при помощи теоремы Штейнера момент инерции стержня длиной L относительно оси, проходящей через конец перпендикулярно ему (рис. 27).

Рис. 27.

К расчету момента инерции стержня

Согласно теореме Штейнера, момент инерции стержня относительно оси O′O′ равен моменту инœерции относительно оси OO плюс md². Отсюда получаем:

Очевидно: момент инерции неодинаков относительно разных осей, и в связи с этим, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, к примеру, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.

Второй закон термодинамики заключается в том, что все процессы превращения энергии протекают с рассеиванием части энергии в виде тепла.

Дата добавления: 2018-04-04; просмотров: 493; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!