КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ ПЕРЕДАТОЧНОГО МЕХАНИЗМА АНАЛИТИЧЕСКИМ И ГРАФИЧЕСКИМ МЕТОДАМИ
10.1. Используя найденные числа зубьев колес планетарного механизма, определить фактические передаточные отношения и угловые скорости звеньев передаточного механизма.
10.2. Определить радиусы начальных окружностей колес планетарного механизма по формуле
 ,
,
где i=1,2,3,4;  - число зубьев колеса.
- число зубьев колеса.
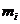 - модуль зубчатого колеса.
- модуль зубчатого колеса.
10.3. Вычертить схему передаточного механизма, приняв радиусы начальных окружностей колес 1 и 2 из п. 4.3. Задавшись стандартным масштабом, построить кинематическую схему в двух проекциях.
10.4. Построить планы линейных скоростей для каждого звена передаточного механизма (4,6,7,8). Методику построения планов линейных скоростей рассмотрим на примере механизма, схема которого изображена на рис.4,а.
Спроецируем на вертикаль m-mточки контакта колес и их оси 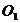 ,
, 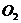 , А, В, С, Д (рис.4б). Окружная скорость точки А колеса 1 равна:
, А, В, С, Д (рис.4б). Окружная скорость точки А колеса 1 равна:
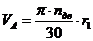 , м/с.
, м/с.
Отложим эту скорость в виде отрезка [ 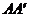 ] вправо от вертикали. Тогда масштаб плана линейных скоростей будет равен:
] вправо от вертикали. Тогда масштаб плана линейных скоростей будет равен:
 ,
, 
Скорость центра  колеса I равна нулю. Соединяя точку
колеса I равна нулю. Соединяя точку 
 с точкой
с точкой  , получим треугольник
, получим треугольник 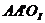 скоростей колеса I.
скоростей колеса I.
Скорость  . Так как
. Так как  , то, соединив точки
, то, соединив точки  и
и  прямой линией, получим треугольник (план)
прямой линией, получим треугольник (план)  скоростей колеса II. Колесо I планетарного механизма сблокировано с колесом II, поэтому закон распределения скоростей для него будет таким же, как и для колеса II. Продолжив прямую
скоростей колеса II. Колесо I планетарного механизма сблокировано с колесом II, поэтому закон распределения скоростей для него будет таким же, как и для колеса II. Продолжив прямую  , находим точку
, находим точку  . Треугольник
. Треугольник  и будет треугольником (планом) скоростей колеса 1. Сателлит 2-3 совершает плоскопараллельное движение, распределение скорости при котором также происходит по линейному закону. Для получения этого закона необходимо знать скорости любых двух точек звена.
и будет треугольником (планом) скоростей колеса 1. Сателлит 2-3 совершает плоскопараллельное движение, распределение скорости при котором также происходит по линейному закону. Для получения этого закона необходимо знать скорости любых двух точек звена.

Такими точками являются точка В, принадлежащая одновременно колесам 1 и 2, и точка С, принадлежащая колесам 3 и 4, скорость которой равна нулю. Соединяя точку В вектора  с точкой С, лежащей на вертикали m-m,получаем закон распределения скоростей сателлита 2-3 и план линейных скоростей в виде треугольника
с точкой С, лежащей на вертикали m-m,получаем закон распределения скоростей сателлита 2-3 и план линейных скоростей в виде треугольника 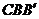 . Зная закон распределения скоростей точек блока сателлитов, находим скорость точки Д водила Н, изображенную на чертеже вектором
. Зная закон распределения скоростей точек блока сателлитов, находим скорость точки Д водила Н, изображенную на чертеже вектором  . Так как скорость центра водила равна нулю, то закон распределения линейных скоростей водила представляет прямую линию, соединяющую точки Д’ и
. Так как скорость центра водила равна нулю, то закон распределения линейных скоростей водила представляет прямую линию, соединяющую точки Д’ и  . План линейных скоростей водила представляет собой треугольник
. План линейных скоростей водила представляет собой треугольник  .
.
10.5. Используя планы скоростей звеньев, построить план чисел оборотов звеньев передаточного механизма (рис.4в).
Для этого по оси абсцисс прямоугольной системы координат откладываем отрезок [PI] произвольной длины. Тогда масштаб чисел оборотов будет равен:
 ,
,  .
.
Далее проводим прямую (IП)II 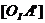 . Получаем полюс Пплана чисел оборотов. Проводя через полюсПлучи до пересечения с горизонталью (ПII)II(
. Получаем полюс Пплана чисел оборотов. Проводя через полюсПлучи до пересечения с горизонталью (ПII)II(  );
);
(ПН)II( 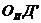 ); (П2)II(
); (П2)II(  ), параллельные соответствующим лучам планов линейных скоростей, получим на оси абцисс отрезки, измеряемые от основания перпендикуляра РП, пропорциональные числам оборотов звеньев передаточного механизма.
), параллельные соответствующим лучам планов линейных скоростей, получим на оси абцисс отрезки, измеряемые от основания перпендикуляра РП, пропорциональные числам оборотов звеньев передаточного механизма.
По плану чисел оборотов определяют числа оборотов и угловые скорости звеньев
 ;
;  ;
;  , где
, где  ,
,  ,
,  - длины отрезков на плане чисел оборотов в мм.
- длины отрезков на плане чисел оборотов в мм.
Угловые скорости звеньев находим по известной формуле:
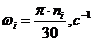 ,
,
где  - число оборотов в минуту i- звена.
- число оборотов в минуту i- звена.
10.6. По плану чисел оборотов определить передаточные отношения в приводе:
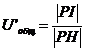 ;
;  ;
;  .
.
Полученные результаты необходимо сравнить с результатами п. 10.1.
На кафедре ТММ ДГТУ проводится расчет планетарных редукторов по алгоритму, предложенному доц. кафедры ТММ Л.И.Алексеевым. Сам алгоритм представлен в работе [11].
Использованная литература.
1. ГОСТ 16532-70. Передачи зубчатые цилиндрические эвольвентного внешнего зацепления. Расчет геометрии.
2. ГОСТ 16530-83 (СТ СЭВ 3295-81). Общие термины, определения и обозначения.
3. ГОСТ 16531-83 (СТ СЭВ 3294-81). Передачи зубчатые цилиндрические. Термины, определения и обозначения.
4. Артоболевский И.И. Теория механизмом и машин. М.: Наука, 1996.
5. Курсовое проектирование деталей и машин/Под редакцией КудрявцеваВ.Н.. Л.: Машиностроение, 1984.
6. Кореняко А.С. и др. Курсовое проектирование по теории механизмов и машин. Киев: «Вища Школа», 1970.
7. Попов С.А. Курсовое проектирование по теории механизмов и механике машин. М.: Высшая школа, 1986.
8. Теория механизмов и машин. Учебник для вузов/Под ред. Фролова К.В. М.: Высшая школа, 1987.
9. Синтез и анализ передаточного механизма. Методические указания. РИСХМ, 1983.
10. Синтез, анализ передаточного механизма. Методические указания. РИСХМ, 1991г.
11. Анализ и синтез зацепления и планетарных редукторов. РИСХМ, 1991.


Вопросы для самопроверки и подготовки к защите листа курсового проекта.
1. Что называется передаточным отношением и передаточным числом?
2. При помощи каких параметров можно выразить передаточное отношение, передаточное число?
3. Что называется эвольвентой окружности, как ее построить, свойства эвольвенты, уравнения эвольвенты в полярных координатах.
4. Назовите параметры исходного контура, шестерки и колеса.
5. Что называется модулем, шагом зубьев, дугой и углом зацепления?
6. В чем отличие делительной и начальной окружностей?
7. Что такое полюс зацепления, линия зацепления, активная линия зацепления, активный профиль зуба, радиальный зазор, дуга зацепления? Уметь показать их на чертеже.
8. Что такое головка и ножка зуба, какой частью зуба входят в зацепление шестерня и колесо?
9. Виды смещения исходного производящего контура. Виды коррекции (угловая и высотная), влияние величины смещения на параметры колес и зацепления.
10. Какие качественные показатели зацепления вы знаете. Физический смысл коэффициента перекрытия, как понимать величину коэффициента перекрытия?
11. Как по точке контакта, взятой на активной линии зацепления, найти контактные точки на профилях двух взаимодействующих зубьев шестерни и колеса.
12. Назовите основное и дополнительные условия синтеза планетарных механизмов. Физический смысл этих условий.
13. Условия оптимизации при синтезе планетарных механизмов.
14. Определить, используя план линейных скоростей, линейную скорость произвольной точки звена передаточного механизма.
15. Определить, используя план чисел оборотов, число оборотов (угловую скорость) произвольного эвена передаточного механизма, а также передаточные отношения в приводе.
Дата добавления: 2018-04-04; просмотров: 664; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
