Формулы ошибки репрезентативности для собственно случайного отбора
Практическое занятие Расчет ошибки выборки, показателей генеральной совокупности, объема выборки
Генеральная совокупность
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и времени. Примеры генеральных совокупностей
· Все жители Москвы (10,6 млн. человек по данным переписи 2002 года)
· Мужчины-Москвичи (4,9 млн. человек по данным переписи 2002 года)
· Юридические лица России (2,2 млн. на начало 2005 года)
· Розничные торговые точки, осуществляющие продажу продуктов питания (20 тысяч на начало 2008 года) и т.д.
Выборка (Выборочная совокупность)
Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности.
Репрезентативность выборки
Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей.
Пример:
· Выборка, целиком состоящая из москвичей, владеющих автомобилем, не репрезентирует все население Москвы.
|
|
|
· Выборка из российских предприятий численностью до 100 человек не репрезентирует все предприятия России.
· Выборка из москвичей, совершающих покупки на рынке, не репрезентирует покупательское поведение всех москвичей.
В то же время, указанные выборки (при соблюдении прочих условий) могут отлично репрезентировать москвичей-автовладельцев, небольшие и средние российские предприятия и покупателей, совершающих покупки на рынках соответственно.
Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от ошибки никак не зависит от размера выборки.
Пример:
Как бы мы не увеличивали количество опрошенных москвичей-автовладельцев, мы не сможем репрезентировать этой выборкой всех москвичей.
Ошибка выборки (доверительный интервал)
Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности.
Ошибка выборки бывает двух видов – статистическая и систематическая. Статистическая ошибка зависит от размера выборки. Чем больше размер выборки, тем она ниже.
Пример:
Для простой случайной выборки размером 400 единиц максимальная статистическая ошибка (с 95% доверительной вероятностью) составляет 5%, для выборки в 600 единиц – 4%, для выборки в 1100 единиц – 3% Обычно, когда говорят об ошибке выборки, подразумевают именно статистическую ошибку.
Систематическая ошибка зависит от различных факторов, оказывающих постоянное воздействие на исследование и смещающих результаты исследования в определенную сторону.
Пример:
|
|
|
· Использование любых вероятностных выборок занижает долю людей с высоким доходом, ведущих активный образ жизни. Происходит это в силу того, что таких людей гораздо сложней застать в каком-либо определенном месте (например, дома).
· Проблема респондентов, отказывающихся отвечать на вопросы анкеты (доля «отказников» в Москве, для разных опросов, колеблется от 50% до 80%)
В некоторых случаях, когда известны истинные распределения, систематическую ошибку можно нивелировать введением квот или перевзвешиванием данных, но в большинстве реальных исследований даже оценить ее бывает достаточно проблематично.
Типы выборок
Выборки делятся на два типа:
· вероятностные
· невероятностные
1. Вероятностные выборки
1.1 Случайная выборка (простой случайный отбор)
Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов, наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел.
1.2 Механическая (систематическая) выборка
Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер генеральной совокупности, при этом – N=n*k
1.3 Стратифицированная (районированная)
Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы (страты). В каждой страте отбор осуществляется случайным или механическим образом.
1.4 Серийная (гнездовая или кластерная) выборка
При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются случайным образом. Объекты внутри групп обследуются сплошняком.
|
|
|
2.Невероятностные выборки
Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д..
2.1. Квотная выборка
Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60 лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки используются в маркетинговых исследованиях достаточно часто.
2.2. Метод снежного кома
Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.)
2.3 Стихийная выборка
Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов.
2.4 Выборка типичных случаев
Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает проблема выбора признака и определения его типичного значения.
|
|
|
Вычисление ошибки репрезентативности для собственно случайной выборки.
Пусть нам необходимо оценить средний возраст некоторой группы людей по ограниченному числу наблюдений n. Оценкой среднего значения непрерывной случайной величины является математическое ожидание:
.
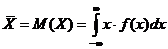Естественной оценкой математического ожидания является среднее арифметическое:
.
От оценки необходимо потребовать следующие свойства:
1. состоятельность – оценка называется состоятельное, если при увеличении числа опытов оценка сходится по вероятности с искомым параметром,
2. несмещенность – оценка называется несмещенной, если выполнялось условие
,
3. эффективность – оценка называется эффективной, если ее дисперсия минимальна по сравнению с другими.
Среднее арифметическое обладает этими свойствами[1].
Оценка параметра является функцией от случайных величин 
, 
, … , 
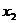, поэтому сама является случайной величиной. Другими словами, мы можем сделать множество выборок, для каждой из которых значение оценки будет различно. По закону больший чисел распределение оценки является нормальным с математическим ожиданием
и дисперсией
[2],
где 
- генеральная дисперсия.
Тогда можно рассчитать вероятность того, что 
попадет в интервал 
. Поскольку нам неизвестна величина 
, то мы будем говорить о вероятности, с которой интервал 
накроет . Эта которая равна площади под графиком функции распределения случайной величины (см. рис. 2):
.
Рисунок 1. Распределение выборочной оценки среднего.
Приведем это распределение к стандартному виду.
Произведем замену переменной:
.
Справа получили функцию Лапласа, которая табулирована (см. Приложение):
.
Нам не известно значение 
, поэтому заменим его на 
. Но в этом случае нужно использовать не нормальное распределение, а распределение Стьюдента.
,
где 
При больших объемах выборки вид распределения Стьюдента приближается к виду нормального распределения, поэтому для больших выборок также можно использовать функцию Лапласа.
Для повторной выборки
(1).
Для бесповторной выборки необходимо внести поправку на конечность ГС
(2).
Для большой ГС (объем ВС составляет менее 5% от ГС) поправкой на конечность совокупности можно пренебречь.
Про коэффициент доверия 
следует сказать отдельно. Этот коэффициент исследователь выбирает сам. Чем меньше , тем меньше доверительный интервал, но тем меньше и вероятность того, что оценка не выйдет за пределы доверительного интервала.
Пример 1. Пусть была произведена выборка 1600 человек. Средний возраст по выборке – 30 лет, среднеквадратическое отклонение – 10 лет. Необходимо найти доверительный интервал.
Прежде всего, необходимо задать надежность оценки. Возьмем 95% надежность. Поскольку выборка большая, воспользуемся таблицей значений функции Лапласа и найдем коэффициент доверия - 1,96.
Тогда
.
С вероятностью 95% истинное средний возраст по ГС находится в интервале от 29,51 лет до 30,49 лет.
Для биномиального распределения
,
где 
– доля признака, 
.
Тогда для повторной выборки из (1)
(3),
для бесповторной выборки из (2)
(4).
Пример 2.Из 200 опрошенных 55% - женщины. Действуем аналогично примеру 1. Выборку также можно считать большой. Тогда =1,96 для 95% надежности.
.
С вероятностью 95% доля женщин в ГС находится в интервале от 48% до 62%.
Формулы ошибки репрезентативности для собственно случайного отбора.
| Предмет изучения. | Повторный отбор. | Бесповторный отбор. |
| Среднее значение признака. | 
| 
|
| Доля признака. | 
| 
|
Где:
z – коэффициент доверия,
n – объем выборки,
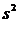- выборочная дисперсия,
N – объем генеральной совокупности,
- доля признака в выборочной совокупности.
Определение объема выборки.
Определение объема выборки – это задача, обратная решенной выше задачи вычисления ошибки выборки.
Формулы для вычисления объема выборки при случайном отборе – просто преобразованные формулы ошибки репрезентативности. Они представлены в таблице 4.
Таблица 2.
Дата добавления: 2018-04-04; просмотров: 1307; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!