Формулы ошибки репрезентативности для стратифицированной выборки (непропорциональный отбор)
| Предмет изучения. | Повторный отбор. | Бесповторный отбор. |
| Среднее значение признака. | 
| 
|
| Доля признака. | 
| 
|
Где:
- объем страты в генеральной совокупности.
- объем страты в выборке.
Как видно из формул, при непропорциональном отборе вместо средней внутригрупповых дисперсий берется сумма взвешенных по объему генеральной совокупности внутригрупповых дисперсий.
Стратифицированная выборка может проводиться пропорционально дисперсии признака в группах. Формулы ошибки репрезентативности для этого случая представлены в таблице 9.
Таблица 9.
Формулы ошибки репрезентативности для стратифицированной выборки (пропорционально колеблемости признака в группах).
| Предмет изучения. | Повторный отбор. | Бесповторный отбор. |
| Среднее значение признака. | 
| 
|
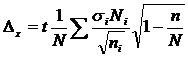
| Доля признака. | 
| 
|
Эти формулы являются просто преобразованными формулами ошибки репрезентативности для непропорционального отбора. Преобразование производится путем подстановки вместо выражения, которое будет представлено немного ниже.
Определение объема выборки.
Формулы для вычисления объема выборки за исключением отбора пропорционально дисперсии — легко получаются путем элементарных преобразований из формул ошибки репрезентативности.
Таблица 10.
Формулы для определения объема выборки при пропорциональном стратифицированном отборе.
|
|
|
| Предмет изучения. | Повторный отбор. | Бесповторный отбор. |
| Среднее значение признака. | 
| 
|
| Доля признака. | 
| 
|
Для непропорционального отбора число опрашиваемых в каждой страте определяется отдельно, исходя из их численности в генеральной совокупности.
Отбор пропорционально колеблемости признака в группе вносит и другой критерий для определения величены страт в выборке – внутригрупповую дисперсию.
Таблица 11.
Формулы для определения объема выборки при стратифицированном отборе пропорционально колеблемости признака в группе.
| Среднее значение признака. | 
|
| Доля признака. | 
|
Плюсы и минусы стратифицированного отбора.
Стратифицированная выборка в любом случае оказывается точнее собственно-случайной. Этот метод особенно хорош, когда генеральная совокупность неоднородна. В этом случае собственно-случайный отбор крайне неэффективен (требует большого объема выборки).
Однако стратифицированная выборка может быть применена лишь при наличии дополнительной информации о генеральной совокупности (например, нам необходимо процентное соотношение мужчин и женщин, в случае, если мы хотим стратифицировать выборку по полу). Отсутствие такой информации делает применение стратифицированной выборки невозможным. Еще один недостаток стратифицированного отбора – это возможность систематической ошибки. Далее на примерах попытаемся проиллюстрировать различные способы применения стратифицированной выборки.
|
|
|
Пример: Возьмем опять данные о доходах из таблицы 1. Только теперь из этого же массива произведем не случайную, а стратифицированную выборку из четырех человек.
Для возможности проведения стратифицированной выборки сделаем допущение, что из предыдущей переписи мы знаем доходы респондентов за предыдущий период и имеем основания предполагать, что к этому периоду они не изменились или изменились пропорционально.
На основании этих данных можно стратифицировать генеральную совокупность по доходу. Результаты этого деления представлены в таблице 12.
Таблица 12.
Дата добавления: 2018-04-04; просмотров: 471; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!