Пространственные преобразования
Способность визуализировать или изображать пространственный объект является основой для понимания формы этого объекта. Кроме того, во многих случаях для этого важна способность вращать, переносить и строить виды проекций объекта. Чтобы понять форму объекта следует вращать объект, отодвигать на расстояние вытянутой руки, передвигать вверх и вниз, вперед и назад и т. д. Чтобы сделать то же самое с помощью компьютера, необходимо распространить предшествующий двумерный анализ на три измерения. Основываясь на полученном опыте, немедленно ввести однородные координаты. Таким образом, точка в трехмерном пространстве [хуz] представляется четырехмерным вектором
 ,
,
где [Т] является матрицей некоего преобразования. Как и ранее, преобразование их однородных координат в обычные задается формулой
 . (4.61)
. (4.61)
Обобщенную матрицу преобразования размерности 4´4 для трехмерных однородных координат можно представить в следующем виде:
 . (4.62)
. (4.62)
Матрицу преобразования из (4.62) можно разделить на четыре отдельные части:

Верхняя левая (3´3)-подматрица задает линейное преобразование, проводящее линейную комбинацию векторов в ту же самую линейную комбинацию преобразования векторов, в форме масштабирования, сдвига, отражения и вращения. Левая нижняя (1´3)-подматрица задает перемещение, а правая верхняя (3´1)- подматрица – перспективное преобразование. Последняя правая нижняя (1´1)-подматрица задает общее масштабирование. Общее преобразование, полученное после применения этой (4´4)-матрицы к однородному вектору и вычисления обычных координат, называется билинейным преобразованием – результат двух последовательных линейных преобразований. В общем случае данное преобразование осуществляет комбинацию сдвига, локального масштабирования, вращения, отражения, перемещения, перспективного преобразования и общего масштабирования.
Трехмерное масштабирование
Диагональные элементы (4´4)-матицы обобщенного преобразования задают локальное и общее масштабирование. Для иллюстрации этого рассмотрим преобразование
 , (4.63)
, (4.63)
которое показывает действие локального масштабирования.
Рассмотрим прямоугольный параллелепипед RРР (рис. 4.17, а) со следующими однородными координатами вершин:
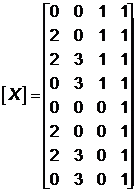 .
.
Чтобы получить единичный куб из RPP с помощью локального масштабирования, необходимы масштабные множители 1/2, 1/3, 1 вдоль осей х, у, z соответственно (рис. 4.17, б). Преобразование локального масштабирования задается матрицей
 .
.
На рис. 4.17, в показано общее изменение масштаба за счет изменения правой нижней подматрицы:
 .
.

Рис. 4.17
Простой трехмерный сдвиг единичного куба выполняется с помощью матрицы преобразования:
 ,
,
т. е. верхняя левая подматрица (3´3) осуществляет сдвиг в трех измерениях.
Если определитель матрицы (3´3) равен +1, то имеет место вращение около начала координат.
Дата добавления: 2018-04-04; просмотров: 735; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
